2003 VI: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
| − | Lisa, Johanna, Christoph | + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> |
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | <center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung 2003'''</big></center> | ||
| + | <center><big>'''Analytische Geometrie VI'''</big></center> | ||
| + | |||
| + | |||
| + | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=ff574c530ac05ed359667c29b75a15ff '''Download der Originalaufgaben: Abitur 2006 LK Mathematik Bayern'''] - [[Media:LKM Abi 2006 I lös.doc|Lösung gesamt]]</center> | ||
| + | |||
| + | |||
| + | <center>Erarbeitet von Lisa Köhler, Johanna Schwarz, Christoph Wacker</center> | ||
| + | <center>[[gesamte Lösung zum Ausdrucken]]</center> | ||
| + | |||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | In einem kartesischen Koordinatensystem sind die Punkte , A(5|0|1), B(0|4|2) und C(0|0|t) | ||
| + | mit 0 < t < 6 gegeben. | ||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 1 | ||
| + | |||
| + | a) Berechnen Sie für die Gerade AB den Schnittpunkt mit der x<sub>1</sub> x<sub>2</sub>-Ebene sowie ihren Abstand d zur x<sub>3</sub>-Achse. | ||
| + | |||
| + | (Teilergebnis: d<math>\frac{20}{\sqrt{41} }</math> ) | ||
| + | |||
| + | <div align="right"><i>'''7 BE'''</i></div> | ||
| + | <br> | ||
| + | :{{Lösung versteckt| | ||
| + | |||
| + | }} | ||
| + | |||
| + | |||
| + | b) Zeigen Sie, dass der Flächeninhalt des Dreiecks ABC nicht kleiner als 10 ist. | ||
| + | |||
| + | |||
| + | <div align="right"><i>'''3 BE'''</i></div> | ||
| + | <br> | ||
| + | :{{Lösung versteckt| | ||
| + | |||
| + | }} | ||
| + | |||
| + | |||
| + | c) Untersuchen Sie, für welche der zulässigen Werte von t das Dreieck ABC rechtwinklig ist. | ||
| + | |||
| + | |||
| + | <div align="right"><i>'''5 BE'''</i></div> | ||
| + | <br> | ||
| + | :{{Lösung versteckt| | ||
| + | |||
| + | }} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 2 | ||
| + | Ferner ist der Punkt S(0|0|6) gegeben. A´, B´, C´ sind die Spurpunkte der Geraden SA, SB, SC in der Koordinatenebene x<sub>3</sub> = 0. | ||
| + | |||
| + | a) Bestimmen Sie die Koordinaten der Punkte A´, B´, C´. | ||
| + | |||
| + | [Teilergebnis: A´(6|0|0), B´(0|6|0)] | ||
| + | |||
| + | |||
| + | <div align="right"><i>'''4 BE'''</i></div> | ||
| + | <br> | ||
| + | <br> | ||
| + | :{{Lösung versteckt| | ||
| + | |||
| + | }} | ||
| + | |||
| + | b) Legen Sie ein Koordinatensystem an (ganze Seite; Querformat; Koordinatenursprung in der Blattmitte). | ||
| + | Tragen Sie darin die Pyramide A´B´C´S und das Dreieck ABC für t = 3 ein. | ||
| + | |||
| + | |||
| + | <div align="right"><i>'''3 BE'''</i></div> | ||
| + | <br> | ||
| + | :{{Lösung versteckt| | ||
| + | |||
| + | }} | ||
| + | |||
| + | |||
| + | c) Berechnen Sie den Winkel, den die Ebene ABC für t = 3 mit der x<sub>1</sub> x<sub>2</sub>-Ebene bildet. | ||
| + | |||
| + | |||
| + | <div align="right"><i>'''4 BE'''</i></div> | ||
| + | <br> | ||
| + | :{{Lösung versteckt| | ||
| + | |||
| + | }} | ||
| + | |||
| + | |||
| + | d) Ermitteln Sie den Wert von t, für den das Dreieck ABC die Pyramide in zwei volumengleiche Teile zerlegt. | ||
| + | |||
| + | |||
| + | <div align="right"><i>'''6 BE'''</i></div> | ||
| + | <br> | ||
| + | :{{Lösung versteckt| | ||
| + | |||
| + | }} | ||
| + | |||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 3 | ||
| + | Der Schnittpunkt von AB mit A´B´ heißt P, der von AC mit A´C´ bzw. BC mit B´C´ heißt Q<sub>t</sub> bzw. R<sub>t</sub> | ||
| + | (<math>t\neq 1</math> und <math>t\neq 2</math> ). | ||
| + | |||
| + | a) Bringen Sie für t = 3 die genannten Geraden in Ihrer Zeichnung zum Schnitt. | ||
| + | |||
| + | |||
| + | <div align="right"><i>'''2 BE'''</i></div> | ||
| + | <br> | ||
| + | <br> | ||
| + | :{{Lösung versteckt| | ||
| + | |||
| + | }} | ||
| + | |||
| + | b) In Ihrer Zeichnung sollten P, Q<sub>3</sub>, R<sub>3</sub> auf einer Geraden liegen.<br /> | ||
| + | Warum liegen die Punkte P, Q<sub>t</sub> und R<sub>t</sub> stets auf einer Geraden s<sub>t</sub>?(Begründung ohne Rechnung genügt.)<br /> | ||
| + | Beschreiben Sie, welcher besonderen Lage sich die Geraden s<sub>t</sub> für t → 1 bzw. für t → 2 nähern und geben Sie jeweils eine Gleichung der zugehörigen Grenzgeraden an. | ||
| + | |||
| + | |||
| + | <div align="right"><i>'''6 BE'''</i></div> | ||
| + | <br> | ||
| + | :{{Lösung versteckt| | ||
| + | |||
| + | }} | ||
Version vom 4. April 2010, 13:24 Uhr
|
|
|
In einem kartesischen Koordinatensystem sind die Punkte , A(5|0|1), B(0|4|2) und C(0|0|t) mit 0 < t < 6 gegeben. |
a) Berechnen Sie für die Gerade AB den Schnittpunkt mit der x1 x2-Ebene sowie ihren Abstand d zur x3-Achse. (Teilergebnis: d 7 BE
3 BE
5 BE
|
Ferner ist der Punkt S(0|0|6) gegeben. A´, B´, C´ sind die Spurpunkte der Geraden SA, SB, SC in der Koordinatenebene x3 = 0. a) Bestimmen Sie die Koordinaten der Punkte A´, B´, C´. [Teilergebnis: A´(6|0|0), B´(0|6|0)]
4 BE
b) Legen Sie ein Koordinatensystem an (ganze Seite; Querformat; Koordinatenursprung in der Blattmitte). Tragen Sie darin die Pyramide A´B´C´S und das Dreieck ABC für t = 3 ein.
3 BE
4 BE
6 BE
|
Der Schnittpunkt von AB mit A´B´ heißt P, der von AC mit A´C´ bzw. BC mit B´C´ heißt Qt bzw. Rt
( a) Bringen Sie für t = 3 die genannten Geraden in Ihrer Zeichnung zum Schnitt.
2 BE
b) In Ihrer Zeichnung sollten P, Q3, R3 auf einer Geraden liegen.
6 BE
|
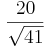 )
)
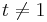 und
und 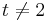 ).
).

