2006 I: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
Zeile 32: Zeile 32:
  
 
:{{Lösung versteckt|
 
:{{Lösung versteckt|
−
folgt demnächst ...
+
[[Bild:Abi_2006_I_Lösung_1a.png|700px]]
 
}}
 
}}
 
<div align="right">3 BE</div>
 
<div align="right">3 BE</div>
Zeile 41: Zeile 41:
  
 
:{{Lösung versteckt|
 
:{{Lösung versteckt|
−
folgt demnächst ...
+
[[Bild:Abi_2006_I_Lösung_1b.png|700px]]
 
}}
 
}}
 
<div align="right">5 BE</div>
 
<div align="right">5 BE</div>
Zeile 49: Zeile 49:
  
 
:{{Lösung versteckt|
 
:{{Lösung versteckt|
−
folgt demnächst ...
+
[[Bild:Abi_2006_I_Lösung_1c.png|700px]]
 
}}
 
}}
 
<div align="right">5 BE</div>
 
<div align="right">5 BE</div>
Zeile 58: Zeile 58:
  
 
:{{Lösung versteckt|
 
:{{Lösung versteckt|
−
folgt demnächst ...
+
[[Bild:Abi_2006_I_Lösung_1d.png|700px]]
 
}}
 
}}
 
<div align="right">4 BE</div>
 
<div align="right">4 BE</div>
Zeile 66: Zeile 66:
  
 
:{{Lösung versteckt|
 
:{{Lösung versteckt|
−
folgt demnächst ...
+
[[Bild:Abi_2006_I_Lösung_1e.png|700px]]
 
}}
 
}}
 
<div align="right">8 BE</div>
 
<div align="right">8 BE</div>

Version vom 28. Februar 2010, 23:06 Uhr


Leistungskurs Mathematik (Bayern): Abiturprüfung 2006
Infinitesimalrechnung I


Download der Originalaufgaben: Abitur 2008 LK Mathematik Bayern - Lösung gesamt


Erarbeitet von Lukas Baumüller, Florian Wilk


Aufgabe 1

Gegeben ist die Funktion f: x→(x-1)\cdotlnx mit der Definitionsmenge D=\mathbb{R}+. Der Graph von f wird mit Gf bezeichnet.
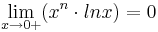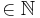Hinweis: \lim_{x\to 0+} (x^n \cdot lnx)=0 für n \in \mathbb{N} , darf ohne Beweis verwendet werden.

a) Geben Sie die Nullstelle von f an und untersuchen Sie das Verhalten von f an den Rändern der Definitionsmenge.

Abi 2006 I Lösung 1a.png

3 BE


b) Weisen Sie nach, dass Gf an der Stelle x=1 einen Punkt mit waagrechter Tangente besitzt. Bestimmen Sie das Monotonieverhalten von f.
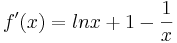[Zur Kontrolle: f'(x)=lnx+1-{1 \over x}]

Abi 2006 I Lösung 1b.png

5 BE


c) Untersuchen Sie das Krümmungsverhalten von Gf . Berechnen Sie f(3) und skizzieren Sie Gf aufgrund der bisherigen Ergebnisse.

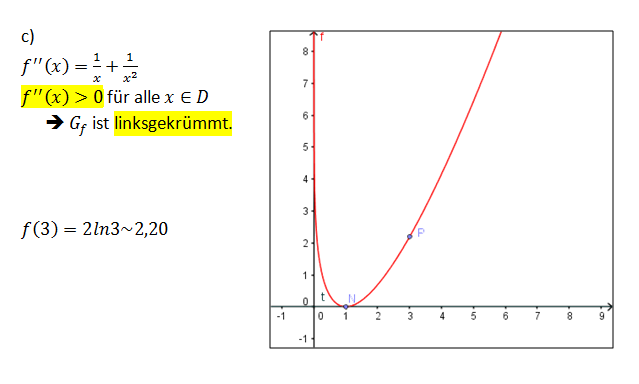
Abi 2006 I Lösung 1c.png

5 BE


d) Begründen Sie, dass f im Intervall ]0;1] umkehrbar ist. Geben Sie Definitions- und Wertemenge der zugehörigen Umkehrfunktion g an.
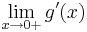Bestimmen Sie \lim_{x\to0+}g'(x) .

Abi 2006 I Lösung 1d.png

4 BE


e) Gf und die Koordinatenachsen begrenzen für x\le1 ein Flächenstück, das sich ins Unendliche erstreckt. Zeigen Sie, dass dieses Flächenstück den endlichen Inhalt 0,75 hat.

Abi 2006 I Lösung 1e.png

8 BE




Aufgabe 2

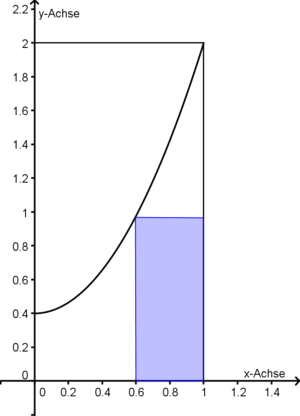
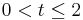Aus rechteckigen Kunststoffplatten von 1 Meter Breite und 2 Meter Höhe wurden Stücke abgeschnitten, wobei die Schnittkurve pt Teil einer Parabel ist, die der Gleichung y=tx2+2-t genügt. Für den Parameter t gilt: 0<t\le2 . In nebenstehender Skizze ist der Fall t=1,6 dargestellt.

Abi 2006 I 2 Graph y.png


a) Zeigen Sie, dass jede Schnittkurve pt durch den Punkt (1/2) verläuft. Beschreiben Sie die Bewegung des Parabelscheitels, wenn t bei 2 beginnend alle Werte des Intervalls ]0;2] durchläuft.

Abi2006ILösung2a.jpeg

3 BE



Aus der Restplatte werden Rechtecke – wie in der Skizze schraffiert dargestellt – ausgeschnitten. Je eine Seite des Rechtecks soll auf dem unteren bzw. auf dem rechten Rand der Platte zu liegen kommen, eine Ecke des Rechtecks soll auf der Schnittkurve liegen.

b) Zeigen Sie, dass für den Inhalt eines solchen Rechtecks gilt
At(x)=-tx3+tx2+(t-2)x+2-t    (0\lex\le1).

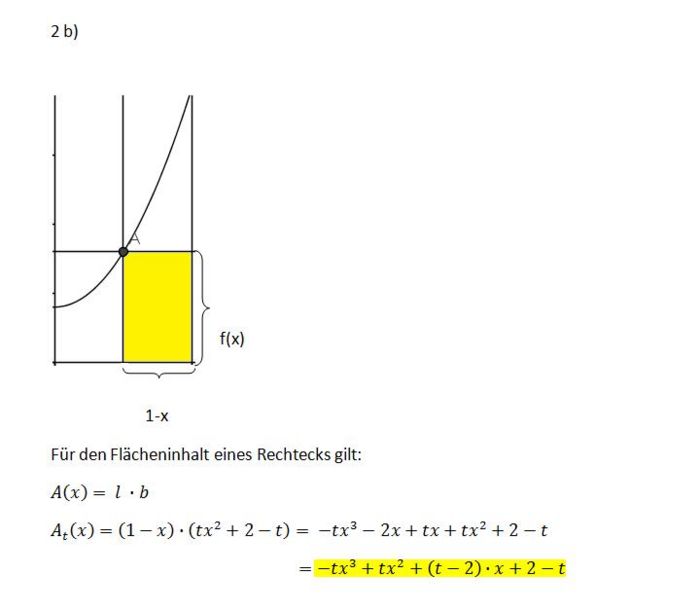
Abi2006ILösung2b.jpeg

3 BE


Der Inhalt des ausgeschnittenen Rechtecks soll möglichst groß sein (Extremwertproblem).

c) Die unten stehende Abbildung zeigt einige Graphen der Scharfunktionen At . Beschreiben Sie, was aufgrund der Abbildung im Fall 0<t<1,5 für die Lösung des Extremwertproblems zu vermuten ist.
Beweisen Sie Ihre Vermutung rechnerisch.

Abi2006ILösung2c.jpeg

6 BE


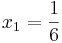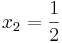d) Im Fall t=1,6 ist die erste Ableitung von At an den Stellen x_1={1 \over 6} und x_2={1 \over 2} gleich Null
(Nachweis nicht erforderlich).
Bestätigen Sie durch Berechnung geeigneter Werte von At , dass für t=1,6 zwei Rechtecke den maximalen Flächeninhalt aufweisen.

Abi2006ILösung2d.jpeg

3 BE



Von „http://rmg.zum.de/index.php?title=LK_Mathematik/Abitur/2006_I&oldid=30273“