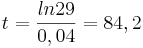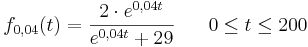Lösung d): Unterschied zwischen den Versionen
Aus RMG-Wiki
(→Berechnen Sie die Höhe einer Sonnenblumenpflanze nach 10, 50 und 150 Tagen) |
(→Berechnen Sie, wann die Wachstumsgeschwindigkeit einer Sonnenblumenpflanze am größten ist) |
||
| Zeile 26: | Zeile 26: | ||
===<u>Berechnen Sie, wann die Wachstumsgeschwindigkeit einer Sonnenblumenpflanze am größten ist</u>=== | ===<u>Berechnen Sie, wann die Wachstumsgeschwindigkeit einer Sonnenblumenpflanze am größten ist</u>=== | ||
<br /> | <br /> | ||
| − | * Die Funktion <math>f_{0,04} (t)\;</math> beschreibt die Höhe der Sonnenblumenpflanze in Abhängigkeit der | + | [[Bild:Graph-facharbeit9.png|400px|right]] |
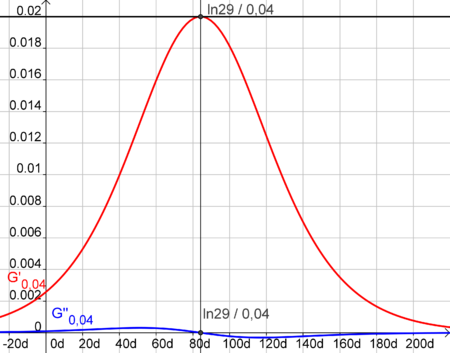
| + | * Die Funktion <math>f_{0,04} (t)\;</math> beschreibt die Höhe der Sonnenblumenpflanze in Abhängigkeit der Zeit t (hier rot zu erkennen) | ||
| − | * Die 1. Ableitung der Funktion <math>f'_{0,04} (t)\;</math> beschreibt die Wachstumsgeschwindigkeit in Abhängigkeit der | + | * Die 1. Ableitung der Funktion <math>f'_{0,04} (t)\;</math> beschreibt die '''Wachstumsgeschwindigkeit''' in Abhängigkeit der Zeit t (hier blau zu erkennen) |
Wenn die Steigung der 1. Ableitung maximal ist, ist die Wachstumsgeschwindigkeit am größten. | Wenn die Steigung der 1. Ableitung maximal ist, ist die Wachstumsgeschwindigkeit am größten. | ||
| + | <br /> | ||
Daraus folgt die Bedingung: <math>f''_{0,04} (t) = 0\;</math> | Daraus folgt die Bedingung: <math>f''_{0,04} (t) = 0\;</math> | ||
| − | + | <br /> | |
| + | [[Bild:Graph-facharbeit8.png| 450px]] | ||
| − | [[ | + | <br /> |
| + | Dies gilt für den Wendepunkt, der bereits in [[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung b)| Teilaufgabe b)]] berechnet und liegt bei <math>t = \frac {ln29} {0,04} = 84,2</math> | ||
===<u>Erläutern Sie die Grenzen dieser mathematischen Modellbildung</u>=== | ===<u>Erläutern Sie die Grenzen dieser mathematischen Modellbildung</u>=== | ||
Version vom 26. Januar 2010, 16:07 Uhr
Durch die Funktion 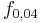 für
für 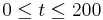 (t in Tagen) kann das Wachstum von Sonnenblumen beschrieben werden, wobei
(t in Tagen) kann das Wachstum von Sonnenblumen beschrieben werden, wobei 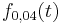 die Höhe (in m) der Pflanzen zur Zeit t bedeutet.
die Höhe (in m) der Pflanzen zur Zeit t bedeutet.
Berechnen Sie die Höhe einer Sonnenblumenpflanze nach 10, 50 und 150 Tagen
Da der Graph der Funktion das Wachstum einer Sonnenblumenpflanze in m beschreibt, wobei die Variable t die Zeit darstellt, muss man lediglich t in die Gleichung einsetzen und erfährt die Höhe in m nach der verstrichenen Zeit t.
Höhe nach 10 Tagen:
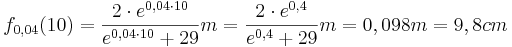
Höhe nach 50 Tagen:
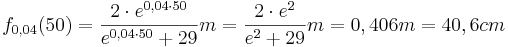
Höhe nach 150 Tagen:
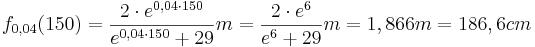
Berechnen Sie, wann die Wachstumsgeschwindigkeit einer Sonnenblumenpflanze am größten ist
- Die Funktion
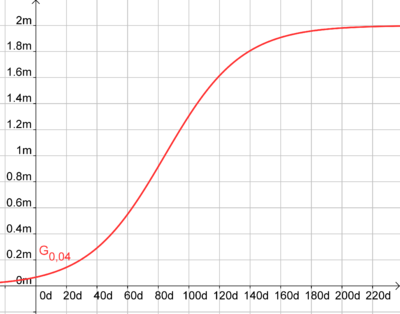
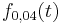 beschreibt die Höhe der Sonnenblumenpflanze in Abhängigkeit der Zeit t (hier rot zu erkennen)
beschreibt die Höhe der Sonnenblumenpflanze in Abhängigkeit der Zeit t (hier rot zu erkennen)
- Die 1. Ableitung der Funktion
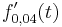 beschreibt die Wachstumsgeschwindigkeit in Abhängigkeit der Zeit t (hier blau zu erkennen)
beschreibt die Wachstumsgeschwindigkeit in Abhängigkeit der Zeit t (hier blau zu erkennen)
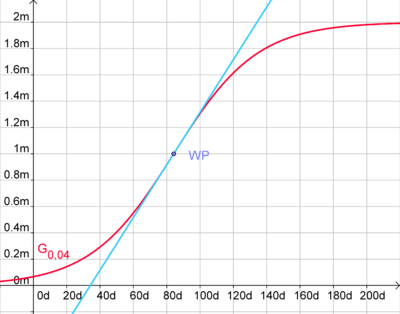
Wenn die Steigung der 1. Ableitung maximal ist, ist die Wachstumsgeschwindigkeit am größten.
Daraus folgt die Bedingung: 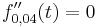
Dies gilt für den Wendepunkt, der bereits in Teilaufgabe b) berechnet und liegt bei