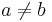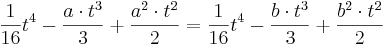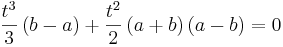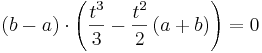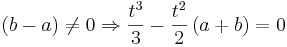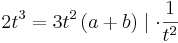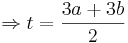Flächengleichheit: Unterschied zwischen den Versionen
Aus RMG-Wiki
("Mal" Zeichen verändert) |
|||
| Zeile 30: | Zeile 30: | ||
::F<sub>a</sub> (t) = F<sub>b</sub> (t) | ::F<sub>a</sub> (t) = F<sub>b</sub> (t) | ||
| − | ::<math>\frac{1}{16}t^4 - \frac{a | + | ::<math>\frac{1}{16}t^4 - \frac{a\cdot t^3}{3} + \frac{a^2\cdot t^2}{2} = \frac{1}{16}t^4 - \frac{b\cdot t^3}{3} + \frac{b^2 \cdot t^2}{2}</math> |
::<math>\frac{t^3}{3} \left( b - a \right) + \frac{t^2}{2} \left( a + b\right) \left( a - b \right) = 0</math> | ::<math>\frac{t^3}{3} \left( b - a \right) + \frac{t^2}{2} \left( a + b\right) \left( a - b \right) = 0</math> | ||
| − | ::<math>\left( b - a \right) | + | ::<math>\left( b - a \right) \cdot \left( \frac{t^3}{3} - \frac{t^2}{2} \left( a + b \right) \right) = 0</math> |
::<math>\left( b - a \right) \neq 0 \Rightarrow \frac{t^3}{3} - \frac{t^2}{2} \left( a + b \right) = 0</math> | ::<math>\left( b - a \right) \neq 0 \Rightarrow \frac{t^3}{3} - \frac{t^2}{2} \left( a + b \right) = 0</math> | ||
| − | ::<math>2 t^3 = 3 t^2 \left( a + b \right) | + | ::<math>2 t^3 = 3 t^2 \left( a + b \right) \mid \cdot \frac{1}{t^2}</math> |
::<math>\Rightarrow t = \frac{3a+3b}{2} </math> | ::<math>\Rightarrow t = \frac{3a+3b}{2} </math> | ||
Version vom 27. Januar 2010, 14:49 Uhr
Aufgabe: Flächengleichheit zweier Funktionen
Betrachte nun zwei unterschiedliche Funktionen fa1 und fa2. Es soll der Zeitpunkt bestimmt werden, zu dem für beide Funktionsannahmen (seit t = 0) genau gleich viel Wasser durch den Fluss geflossen wäre.
|
|
- Im Weiteren wird eine Funktion mit Parameter a, die andere mit Parameter b bezeichnet. Dabei gilt:
- Fa (t) = Fb (t)
- Somit sind zwei Funktionen Fa und Fb flächenmäßig gleich groß, wenn für frei wählbares a und b gilt, dass sie bis
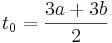 integriert werden. Bei t0 handelt es sich um die obere Integrationsgrenze.
integriert werden. Bei t0 handelt es sich um die obere Integrationsgrenze.