Teilaufgabe a: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
Zeile 1: Zeile 1:
−
Für jede reelle Zahl a sei eine Funktion '''f<sub>a</sub>''' durch <math>y  = f_a (x) = ( x - a )\cdot e^{a+2-x}</math> mit <math>x\in R</math> gegeben.
+
Für jede reelle Zahl a sei eine Funktion <math>f_a\,</math> durch <math>y  = f_a (x) = ( x - a )\cdot e^{a+2-x}</math> mit <math>x\in R</math> gegeben.
  
  
−
:1.Untersuchen Sie den Graphen von '''f<sub>a</sub>''' auf:
+
:1.Untersuchen Sie den Graphen von <math>f_a\,</math> auf:
 
::*Schnittpunkte mit den Koordinatenachsen,<br />[[Facharbeit Andre Etzel/Teilaufgabe a/Lösung: Schnittpunkte mit den Koordinatenachsen|Lösung: Schnittpunkte mit den Koordinatenachsen]]
 
::*Schnittpunkte mit den Koordinatenachsen,<br />[[Facharbeit Andre Etzel/Teilaufgabe a/Lösung: Schnittpunkte mit den Koordinatenachsen|Lösung: Schnittpunkte mit den Koordinatenachsen]]
 
::*lokale Extrempunkte und<br /> [[Facharbeit Andre Etzel/Teilaufgabe a/Lösung: lokale Extrempunkte|Lösung: lokale Extrempunkte]]
 
::*lokale Extrempunkte und<br /> [[Facharbeit Andre Etzel/Teilaufgabe a/Lösung: lokale Extrempunkte|Lösung: lokale Extrempunkte]]
Zeile 21: Zeile 21:
 
<ggb_applet width="773" height="460"  version="3.2" ggbBase64="UEsDBBQACAAIAMGmNzwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1szVbfb9s2EH5u/wpCT0m72JJspwlgp9i6hxVI2wdvfdhDAUo6WVwoUSCpRM5f3+ORtB0364IuGPZgSLw734/vvjtq+XZsJbsFbYTqVkk2SRMGXakq0W1WyWDrs4vk7dXL5QbUBgrNWa10y+0qmU3yxMkHcfXyxdI06o5xSSafBdytEqsHSJjpNfDKNADWi2suDcr5MAopuN5+Kv6C0pq9wvt43/WDjU7KtroWJh6nFK+Xwv4qbkUFmklVrpLzBWaOb59BW1FyuUrmqZfkWNb5QyWKZk7bKC3uVWed+d55jRLGjLgH/GfuZMsp1bmEoZSiErxzxVAeaMTYnahsgymkb9AliE2Duc4XF95bqZSu1ltjoWXjn6DVKsmzhcN5608zfzKYFwZcpKQ6PJEbuF2DtdgVw/gIJmKz0aLagecO780vSu5FvRKdfcd7O2jq6CyI1nbr/GMo7fL9udtICLIMEW+gvCnUuPYYzLzr37c9/YXyKTbvlFSaaSxnsUCD8Cz8k2xcojurlGxSsgg+nNOdPrvMyYKehX+SlRSdTy0UnsWqszSGEYY5gUMRiRixkbwAbGzChk7Y63hAAtzsK3X2H4e2wAE4pMDOZfZMLpfTI+4sb0B3ID1DOmzsoAbDbh0TfesojwpK0eLRKwIg3DXrD0zASyvYaIh5+/HxcJE2PWThkXg5jUm4HAzmWlpcA1iPdbW4MbU4Iu6t4tZJ3AxIaAEHxBIbuqEFLcodMjxx0TDEEAJlkcC0IhSN+xGae9hR/Td8wcXQNxzfJllgBd/i6B+WSN4+qCoGDmEl7YhW4HY7o0Fr+YiD5d54YZQcLKxLBLC7ViW3tAV9dmGqs5QmcnQrg0YzzmgtRtgP2uOrZM9d2yBJOjDGtTGAF/nbYY8JeFwSva8RNyeA51+0ZT3WTEO8IwiyynfjH/sCx33JJ2+yi/zC/eaLy3S+eKRLobT/ok0EppccTGG8JR4qHlQ94g1j3OUV06zxAhsRxfpkPGUrdjKyM8ZP2SsGX044e83ySYqS8TRh029Qq4eOJiDZO3tyF5+L3+l3gftU1wasY+MlUfHsfP4orOmT+fd9NJuAZuPRhCeh1vzfUHt+XH4LuBClcMf9xOA0/p0u2MeACoqdi38LAF24PwoB3QjGMSkPa+3blcDuDxa4/25wHzzkZnYM0vTwDqFvpvDNePUVUEsHCBT7mod+AwAAZQoAAFBLAQIUABQACAAIAMGmNzwU+5qHfgMAAGUKAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAuAMAAAAA" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" />}}<br />
 
<ggb_applet width="773" height="460"  version="3.2" ggbBase64="UEsDBBQACAAIAMGmNzwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1szVbfb9s2EH5u/wpCT0m72JJspwlgp9i6hxVI2wdvfdhDAUo6WVwoUSCpRM5f3+ORtB0364IuGPZgSLw734/vvjtq+XZsJbsFbYTqVkk2SRMGXakq0W1WyWDrs4vk7dXL5QbUBgrNWa10y+0qmU3yxMkHcfXyxdI06o5xSSafBdytEqsHSJjpNfDKNADWi2suDcr5MAopuN5+Kv6C0pq9wvt43/WDjU7KtroWJh6nFK+Xwv4qbkUFmklVrpLzBWaOb59BW1FyuUrmqZfkWNb5QyWKZk7bKC3uVWed+d55jRLGjLgH/GfuZMsp1bmEoZSiErxzxVAeaMTYnahsgymkb9AliE2Duc4XF95bqZSu1ltjoWXjn6DVKsmzhcN5608zfzKYFwZcpKQ6PJEbuF2DtdgVw/gIJmKz0aLagecO780vSu5FvRKdfcd7O2jq6CyI1nbr/GMo7fL9udtICLIMEW+gvCnUuPYYzLzr37c9/YXyKTbvlFSaaSxnsUCD8Cz8k2xcojurlGxSsgg+nNOdPrvMyYKehX+SlRSdTy0UnsWqszSGEYY5gUMRiRixkbwAbGzChk7Y63hAAtzsK3X2H4e2wAE4pMDOZfZMLpfTI+4sb0B3ID1DOmzsoAbDbh0TfesojwpK0eLRKwIg3DXrD0zASyvYaIh5+/HxcJE2PWThkXg5jUm4HAzmWlpcA1iPdbW4MbU4Iu6t4tZJ3AxIaAEHxBIbuqEFLcodMjxx0TDEEAJlkcC0IhSN+xGae9hR/Td8wcXQNxzfJllgBd/i6B+WSN4+qCoGDmEl7YhW4HY7o0Fr+YiD5d54YZQcLKxLBLC7ViW3tAV9dmGqs5QmcnQrg0YzzmgtRtgP2uOrZM9d2yBJOjDGtTGAF/nbYY8JeFwSva8RNyeA51+0ZT3WTEO8IwiyynfjH/sCx33JJ2+yi/zC/eaLy3S+eKRLobT/ok0EppccTGG8JR4qHlQ94g1j3OUV06zxAhsRxfpkPGUrdjKyM8ZP2SsGX044e83ySYqS8TRh029Qq4eOJiDZO3tyF5+L3+l3gftU1wasY+MlUfHsfP4orOmT+fd9NJuAZuPRhCeh1vzfUHt+XH4LuBClcMf9xOA0/p0u2MeACoqdi38LAF24PwoB3QjGMSkPa+3blcDuDxa4/25wHzzkZnYM0vTwDqFvpvDNePUVUEsHCBT7mod+AwAAZQoAAFBLAQIUABQACAAIAMGmNzwU+5qHfgMAAGUKAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAuAMAAAAA" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" />}}<br />
  
−
:3.Skizzieren Sie den Graphen der Funktion '''f<sub>2</sub>''' für '''1,6 <u><</u> x <u><</u>7!'''
+
:3.Skizzieren Sie den Graphen der Funktion <math>f_2\,</math> für <math>1,6 \le  x \le 7</math>!
 
{{Lösung versteckt|
 
{{Lösung versteckt|
 
Graph der Funktion f<sub>2</sub> für 1,6 <u><</u> x <u><</u> 7
 
Graph der Funktion f<sub>2</sub> für 1,6 <u><</u> x <u><</u> 7

Version vom 23. Januar 2010, 22:26 Uhr

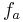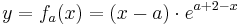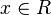Für jede reelle Zahl a sei eine Funktion f_a\, durch y = f_a (x) = ( x - a )\cdot e^{a+2-x} mit x\in R gegeben.


1.Untersuchen Sie den Graphen von 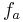f_a\, auf:
Bestimmen Sie gegebenenfalls deren Koordinaten!


2.Alle Extrempunkte liegen auf dem Graphen einer Funktion h. Geben Sie eine Funktionsgleichung von h an!

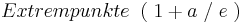
Extrempunkte\; \;(\; 1 + a \;/\; e\; )\;

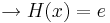
\rightarrow H ( x ) = e

Alle Extrempunkte für 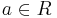a\in R befinde sich auf einer Parallelen zur x-Achse mit y=e\;.
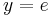Das heißt, dass alle Extrempunkte auf dem Graphen der Funktion 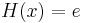H ( x ) = e\; liegen.


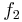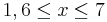3.Skizzieren Sie den Graphen der Funktion f_2\, für 1,6 \le x \le 7!

Graph der Funktion f2 für 1,6 < x < 7


Von „http://rmg.zum.de/index.php?title=Facharbeit_Andre_Etzel/Teilaufgabe_a&oldid=27764“