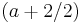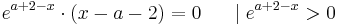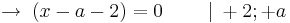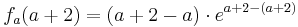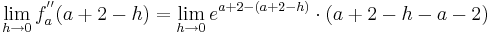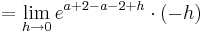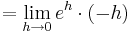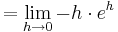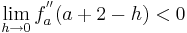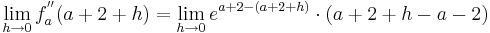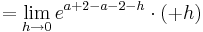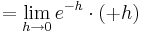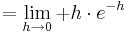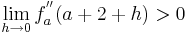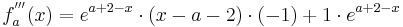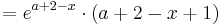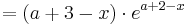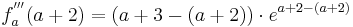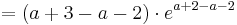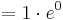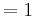Lösung: Wendepunkte: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 39: | Zeile 39: | ||
: <math>\lim_{h\to 0}f_a^{''} ( a + 2 - h ) = \lim_{h\to 0}e^{a + 2 - (a + 2 - h )}\cdot ( a + 2 - h - a - 2 )</math><br /> | : <math>\lim_{h\to 0}f_a^{''} ( a + 2 - h ) = \lim_{h\to 0}e^{a + 2 - (a + 2 - h )}\cdot ( a + 2 - h - a - 2 )</math><br /> | ||
| − | :::::: <math>=\lim_{h\to 0} e^{a + 2 - a- 2 + h }\cdot (- h)</math><br /> | + | ::::::: <math>=\lim_{h\to 0} e^{a + 2 - a- 2 + h }\cdot (- h)</math><br /> |
| − | :::::: <math>= \lim_{h\to 0}e^{h }\cdot ( -h )</math><br /> | + | ::::::: <math>= \lim_{h\to 0}e^{h }\cdot ( -h )</math><br /> |
| − | :::::: <math>= \lim_{h\to 0}-h\cdot e^{h }</math><br /> | + | ::::::: <math>= \lim_{h\to 0}-h\cdot e^{h }</math><br /> |
| − | + | : <math>\lim_{h\to 0}f_a^{''} ( a + 2 - h )<0</math> | |
: <math>\lim_{h\to 0}f_a^{''} ( a + 2 + h ) =\lim_{h\to 0} e^{a + 2 - (a + 2 + h )}\cdot ( a + 2 + h - a - 2 )</math><br /> | : <math>\lim_{h\to 0}f_a^{''} ( a + 2 + h ) =\lim_{h\to 0} e^{a + 2 - (a + 2 + h )}\cdot ( a + 2 + h - a - 2 )</math><br /> | ||
| − | :::::: <math>=\lim_{h\to 0} e^{a + 2 - a- 2 - h }\cdot (+ h)</math><br /> | + | ::::::: <math>=\lim_{h\to 0} e^{a + 2 - a- 2 - h }\cdot (+ h)</math><br /> |
| − | :::::: <math>= \lim_{h\to 0}e^{-h }\cdot ( +h )</math><br /> | + | ::::::: <math>= \lim_{h\to 0}e^{-h }\cdot ( +h )</math><br /> |
| − | :::::: <math>= \lim_{h\to 0}+h\cdot e^{-h }</math><br /> | + | ::::::: <math>= \lim_{h\to 0}+h\cdot e^{-h }</math><br /> |
| − | + | : <math>\lim_{h\to 0}f_a^{''} ( a + 2 + h )>0</math> | |
<math>\rightarrow</math> VZW bei <math>x = a + 2\;</math><br /> | <math>\rightarrow</math> VZW bei <math>x = a + 2\;</math><br /> | ||
Version vom 23. Januar 2010, 01:08 Uhr
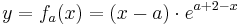 mit
mit 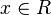 ;
; 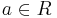
Inhaltsverzeichnis |
Wendepunkte
Zweite Ableitung: siehe Überprüfung des Extrempunkts; 2. Möglichkeit
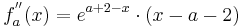
Um mögl. Wendepunkte zu bestimmen benötigt man die zweite Ableitung.
Mögl. Wendepunkte tretten für 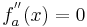 auf.
auf.
Möglicher Wendepunkt bei 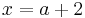
 mög. WP
mög. WP 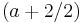
Überprüfung des Wendepunkts
1. Möglichkeit
H-Methode , VZW des Krümmungsverhaltens
 VZW bei
VZW bei 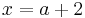
 Wendepunkt bei
Wendepunkt bei 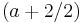
zur Verdeutlichung
| x<2+a | x=2+a | x>2+a | |||
|---|---|---|---|---|---|
| ea + 2 - x | + | + | |||
| ( x - a - 2 ) | - | + | |||
| fa ( x ) | - | + |
 WP
WP 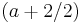
2. Möglichkeit
Verwendung der dritten Ableitung
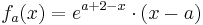
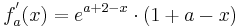
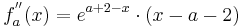
Um die dritte Ableitung zu bekommen muss man hier die Produktregel verwenden.
[Hilfe zur Produktregel]
Wenn die dritte Ableitung am möglichen Wendepunkt ungleich Null ist, liegt ein Wendepunkt vor.
 WP
WP