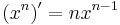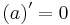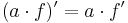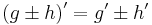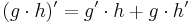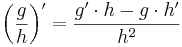Q11 Mathematik: Unterschied zwischen den Versionen
Aus RMG-Wiki
(→7. Newton-Verfahren) |
|||
| Zeile 103: | Zeile 103: | ||
#[http://www.brinkmann-du.de/mathe/gost/diff_01_07.htm#abs2 Musterbeispiele zur Monotonie] | #[http://www.brinkmann-du.de/mathe/gost/diff_01_07.htm#abs2 Musterbeispiele zur Monotonie] | ||
#<font color="green">Interaktiv:</font> [[Q11 Mathematik/Extrema|Extrema: Beispielaufgaben]] | #<font color="green">Interaktiv:</font> [[Q11 Mathematik/Extrema|Extrema: Beispielaufgaben]] | ||
| − | #Lösungen Buch: [[Q11 Mathematik/Seite66_5h|66/5h]] - [[Q11 Mathematik/Seite72_2|72/2]] - [[Q11 Mathematik/Seite73_3|73/3]] - [[Q11 Mathematik/Seite73_4|73/4]] - [[Media:Buch LS11 77 3.pdf|77/3]] - [[Q11 Mathematik/Seite80_21|80/21 | + | #Lösungen Buch: [[Q11 Mathematik/Seite66_5h|66/5h]] - [[Q11 Mathematik/Seite72_2|72/2]] - [[Q11 Mathematik/Seite73_3|73/3]] - [[Q11 Mathematik/Seite73_4|73/4]] - [[Media:Buch LS11 77 3.pdf|77/3]] - [[Q11 Mathematik/Seite80_21|80/21]] |
</td></tr></table></center> | </td></tr></table></center> | ||
| Zeile 115: | Zeile 115: | ||
====7. Newton-Verfahren ==== | ====7. Newton-Verfahren ==== | ||
[[Bild:NewtonIteration Ani.gif|250px|right]] | [[Bild:NewtonIteration Ani.gif|250px|right]] | ||
| + | #[[Q11 Mathematik/Seite88_5b|88/5b]] | ||
| + | #[http://www.mi.uni-koeln.de/~jhorak/geogebra/newton2.html Newtonverfahren mit GeoGebra1] | ||
| + | #[http://commons.wikimedia.org/wiki/File:NewtonIteration_Ani.gif?uselang=de Animation] | ||
| + | # Buch Seite 81 | ||
#[http://www.stephantesch.de/uploads/media/2007_01_19-Newton_Verfahren.pdf Newton Verfahren - Herleitung] | #[http://www.stephantesch.de/uploads/media/2007_01_19-Newton_Verfahren.pdf Newton Verfahren - Herleitung] | ||
| − | + | #[http://www.arndt-bruenner.de/mathe/java/newton.htm Newton-Algorithmus zur Approximation von Nullstellen] | |
| − | + | ||
| − | + | ;Weiteres | |
| − | + | #[http://www.learn-line.nrw.de/angebote/selma/foyer/andereautoren/visnewton/visnewton.htm Visualisierung des Newton-Verfahrens mittels Computers mit Excel] | |
| − | + | #[http://home.eduhi.at/teacher/alindner/Dyn_Geometrie/DiffInt/NewtonNaeherung.htm Das Newtonsche Näherungsverfahren Lindner] | |
| − | + | #[http://www.geogebra.org/de/upload/files/dynamische_arbeitsblaetter/mschulte/Newtonverfahren.ggb Newtonverfahren mit geoGebra2] | |
| + | |||
| + | |||
</td></tr></table></center> | </td></tr></table></center> | ||
</div> | </div> | ||
Version vom 11. Januar 2010, 20:14 Uhr
1. Gebrochenrationale FunktionenLösungen Buch: Lösungen AH: |
2. Differenzenquotient - mittlere Änderungsrate -Steigung Sekante |
3. Differentialquotient - lokale Änderungsrate - Steigung Tangente
|
4. Ableitungsfunktion
|
5. Ableitungsregeln
|
6. Monotonie, Extrema, Funktionsuntersuchung
|