Mathematik Hausaufgabe - Lösung: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
Zeile 11: Zeile 11:
 
2) Flächenberechnung:
 
2) Flächenberechnung:
 
<math>\int_{0}^{3} 1/3x^2+2x+1\,dx</math> = '''9'''
 
<math>\int_{0}^{3} 1/3x^2+2x+1\,dx</math> = '''9'''
 +
 +
 +
Hausaufgabe vom 23.09.2008
 +
S.211/7
 +
 +
Aufgabenstellung: Berechne den Inhalt des Segments, das die Gerade mit der Gleichung y-4=0 vom Graphen der Funktion <math>f(x) = 1/4 x^2</math> abschneidet!
 +
 +
 +
[[Bild:Lösungsanleitung1.png]]
 +
 +
 +
''Lösung''
 +
 +
1. Schnittstellen berechnen: x<sub>1</sub> = -4 ;  x<sub>2</sub> = 4
 +
 +
2. '''A''' = <math>\int_{-4}^{4} f (4-1/4x^2)\,dx</math> = <math>\left[ 4x-1/4 (x^3)/3\right]</math> = ... = '''64/3'''

Version vom 1. September 2009, 19:46 Uhr

Hausaufgabe vom 25.08.2008 AB Infinitesimalrechnung; S.216/10

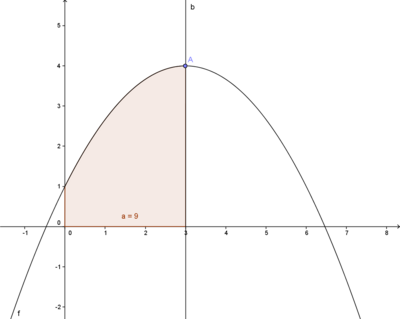
Aufgabenstellung: Wie groß ist die Fläche, die vom Graphen Gf der Funktion f(x)=-1/3x2+2x+1, der Ordinate des höchsten Punktes, der x-Achse und der y-Achse eingeschlossen wird?

Aufgabe10.png

1) Berechnung des Maximums: f´(x)=0; -2/3x+2=0; x=3; Maximum (3/4)

2) Flächenberechnung: 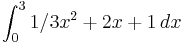\int_{0}^{3} 1/3x^2+2x+1\,dx = 9


Hausaufgabe vom 23.09.2008 S.211/7

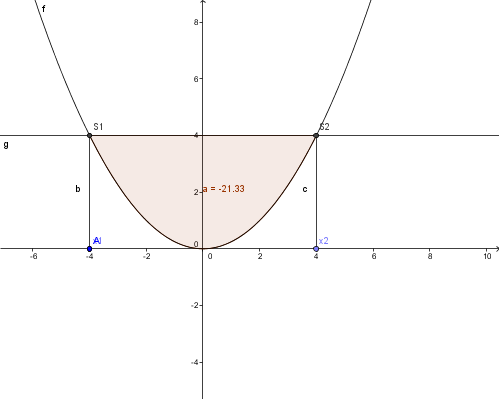
Aufgabenstellung: Berechne den Inhalt des Segments, das die Gerade mit der Gleichung y-4=0 vom Graphen der Funktion 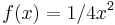f(x) = 1/4 x^2 abschneidet!


Lösungsanleitung1.png


Lösung

1. Schnittstellen berechnen: x1 = -4 ; x2 = 4

2. A = 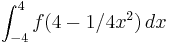\int_{-4}^{4} f (4-1/4x^2)\,dx = \left[ 4x-1/4 (x^3)/3\right] = ... = 64/3

Von „http://rmg.zum.de/index.php?title=Mathematik_Hausaufgabe_-_Lösung&oldid=19662“