Übungen: Unterschied zwischen den Versionen
Aus RMG-Wiki
| (6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | <div style="margin:0px; margin-right:90px; border:thick double green; padding: 1em 1em 1em 1em; background-color:white; width: | + | <div style="margin:0px; margin-right:90px; border:thick double green; padding: 1em 1em 1em 1em; background-color:white; width:60%; align:center; "> |
<span style="color: green">'''Arbeitsauftrag:'''</span> | <span style="color: green">'''Arbeitsauftrag:'''</span> | ||
*Berechne die Flächeninhalte der Dreiecke. | *Berechne die Flächeninhalte der Dreiecke. | ||
*Kontrolliere deine Ergebnisse mit den Ergebnissen auf der Seite. | *Kontrolliere deine Ergebnisse mit den Ergebnissen auf der Seite. | ||
| − | :Anmerkung: ''' | + | :Anmerkung: '''A<sub>Dreieck</sub>=(Grundlinie<math>\cdot</math>Höhe<sub>Grundlinie</sub>) : 2''' |
| + | :1 Kästchen <math>\widehat{=}</math> 1 cm | ||
</div><br /> | </div><br /> | ||
| Zeile 13: | Zeile 14: | ||
| width="50%" style="vertical-align:top" | | | width="50%" style="vertical-align:top" | | ||
| + | <big>Übung 1:</big> | ||
| + | |||
{{Lösung versteckt| | {{Lösung versteckt| | ||
<big>A<math>=</math>(c<math>\cdot</math>h<sub>c</sub>) : 2<math>=</math>(7 cm <math>\cdot</math>6 cm) : 2<math>=</math>21 cm²</big> | <big>A<math>=</math>(c<math>\cdot</math>h<sub>c</sub>) : 2<math>=</math>(7 cm <math>\cdot</math>6 cm) : 2<math>=</math>21 cm²</big> | ||
| Zeile 27: | Zeile 30: | ||
| width="50%" style="vertical-align:top" | | | width="50%" style="vertical-align:top" | | ||
| + | <big>Übung 2:</big> | ||
| + | |||
{{Lösung versteckt| | {{Lösung versteckt| | ||
| − | <big>A<math>=</math>(e<math>\cdot</math>h<sub>e</sub>) : 2<math>=</math>(5 cm <math>\cdot</math> | + | <big>A<math>=</math>(e<math>\cdot</math>h<sub>e</sub>) : 2<math>=</math>(5 cm <math>\cdot</math>6 cm) : 2<math>=</math>15 cm²</big> |
}} | }} | ||
|} | |} | ||
| Zeile 41: | Zeile 46: | ||
| width="50%" style="vertical-align:top" | | | width="50%" style="vertical-align:top" | | ||
| + | <big>Übung 3:</big> | ||
| + | |||
{{Lösung versteckt| | {{Lösung versteckt| | ||
<big>A<math>=</math>(j<math>\cdot</math>h<sub>j</sub>) : 2<math>=</math>(7 cm <math>\cdot</math>4 cm) : 2<math>=</math>14 cm²</big> | <big>A<math>=</math>(j<math>\cdot</math>h<sub>j</sub>) : 2<math>=</math>(7 cm <math>\cdot</math>4 cm) : 2<math>=</math>14 cm²</big> | ||
| Zeile 48: | Zeile 55: | ||
---- | ---- | ||
| − | + | <br> | |
| − | + | ||
| − | + | ||
| − | + | '''Verschiebe den Punkt C nach rechts und links. Beobachte den Flächeninhalt. | |
| + | |||
| + | <ggb_applet width="750" height="300" filename="Dreieck Übung 3.4.ggb" showResetIcon="true" /> | ||
| + | |||
| + | <br> | ||
| + | <br> | ||
| + | |||
| + | <big>Übung 4:</big> | ||
| − | |||
{{Lösung versteckt| | {{Lösung versteckt| | ||
| − | <big>A<math>=</math>( | + | |
| + | <big>A<math>=</math>(c<math>\cdot</math>h<sub>c</sub>) : 2<math>=</math>(5 cm <math>\cdot</math>4 cm) : 2<math>=</math>10 cm²</big> | ||
| + | |||
| + | '''Der Flächeninhalt verändert sich nicht''' | ||
| + | |||
| + | Begründe: | ||
| + | {{versteckt| Alle Dreiecke, die in einer Grundlinie und der dazugehörigen Höhe übereinstimmen, haben den selben Flächeninhalt.}} | ||
| + | |||
}} | }} | ||
| − | + | ||
| + | <br /> | ||
---- | ---- | ||
<big>[[Lernpfad Flächenberechnung/Inhaltsverzeichnis|Hier]]</big> geht's weiter! | <big>[[Lernpfad Flächenberechnung/Inhaltsverzeichnis|Hier]]</big> geht's weiter! | ||
Aktuelle Version vom 26. September 2010, 22:36 Uhr
Arbeitsauftrag:
- Berechne die Flächeninhalte der Dreiecke.
- Kontrolliere deine Ergebnisse mit den Ergebnissen auf der Seite.
- Anmerkung: ADreieck=(Grundlinie
 HöheGrundlinie) : 2
HöheGrundlinie) : 2
- 1 Kästchen
 1 cm
1 cm
|
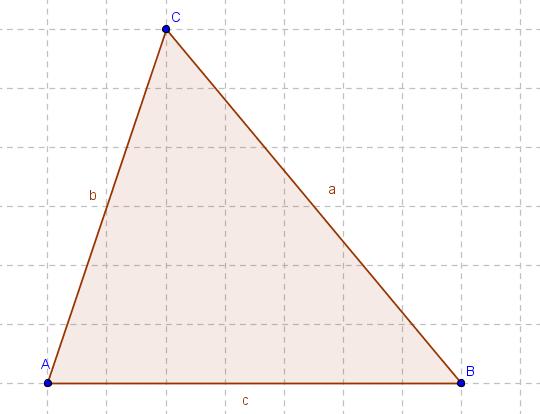
Übung 1:
A |
|
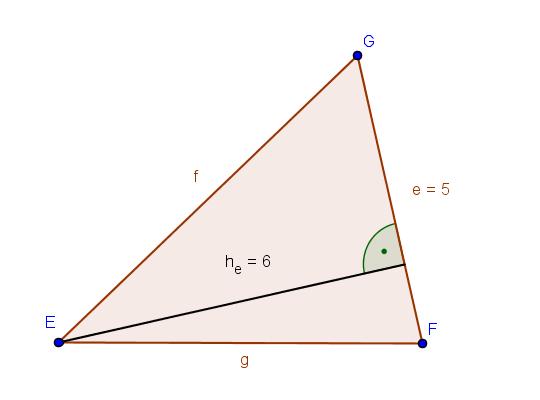
Übung 2:
A |
|
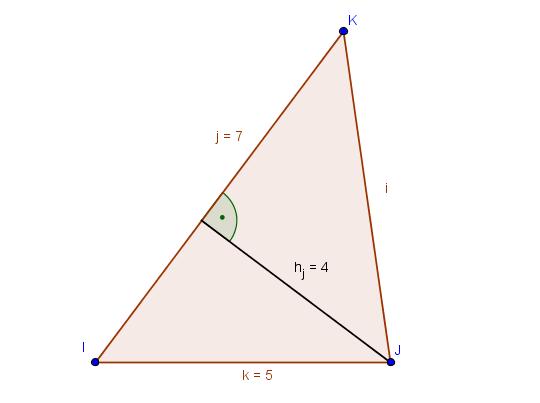
Übung 3:
A |
Verschiebe den Punkt C nach rechts und links. Beobachte den Flächeninhalt.
Übung 4:
A (c
(c hc) : 2
hc) : 2 (5 cm
(5 cm  4 cm) : 2
4 cm) : 2 10 cm²
10 cm²
Der Flächeninhalt verändert sich nicht
Begründe:
Alle Dreiecke, die in einer Grundlinie und der dazugehörigen Höhe übereinstimmen, haben den selben Flächeninhalt.
Hier geht's weiter!