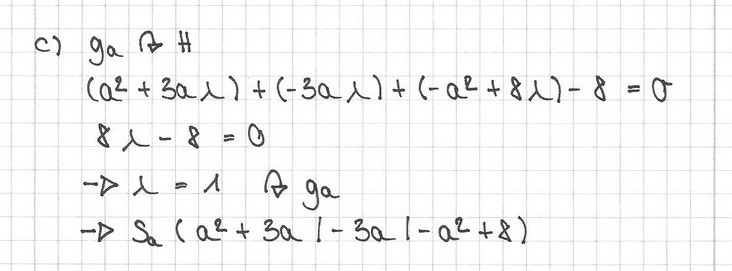2003 V: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: Lea M., Nellie K. und Max B.) |
|||
| (16 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Lea | + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> |
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | <center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung 2003'''</big></center> | ||
| + | <center><big>'''Analytische Geometrie V'''</big></center> | ||
| + | |||
| + | |||
| + | <center>[http://www.isb.bayern.de/isb/index.aspx?MNav=0&QNav=11&TNav=0&INav=0&VTyp=6&Fach=30&VJg=13 '''Download der Originalaufgaben: Abitur 2003 LK Mathematik Bayern'''] - [[Media:LKM Abi 2003 VI lös.pdf|Lösung gesamt]]</center> | ||
| + | |||
| + | |||
| + | <center>Erarbeitet von Nellie Kirchner, Lea Mainberger, Maximilian Benkert</center> | ||
| + | |||
| + | |||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | In einem kartesischen Koordinatensystem des <math>\mathbb{R} </math><sup>3</sup> ist die | ||
| + | Ebene H: x<sub>1</sub> + x<sub>2</sub> + x<sub>3</sub> - 8 = 0 , sowie die Schar von Geraden g<sub>a</sub> : <math>\vec x = \begin{pmatrix} a^2 \\ 0 \\ -a^2 \end{pmatrix} + \lambda \cdot\begin{pmatrix} 3a \\ -3a \\ 8 \end{pmatrix}</math>, <math>\lambda</math> ∈ <math>\mathbb{R} </math> , a ∈ <math>\mathbb{R} </math> gegeben. | ||
| + | |||
| + | |||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 1 | ||
| + | |||
| + | a) Zeigen Sie, dass keine der Geraden g<sub>a</sub> parallel und keine senkrecht zur Ebene H verläuft. | ||
| + | |||
| + | <div align="right"><i>'''3 BE'''</i></div> | ||
| + | <br> | ||
| + | :{{Lösung versteckt|[[Bild:Mainberger_Lea_2003_V_1a.jpg]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | |||
| + | b) Welche dieser Geraden schneidet H unter dem größten Winkel? Berechnen Sie diesen maximalen Winkel auf eine Dezimale genau. | ||
| + | |||
| + | <div align="right"><i>'''6 BE'''</i></div> | ||
| + | <br> | ||
| + | :{{Lösung versteckt|[[Bild:Mainberger_Lea_2003_V_1b_001.jpg]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | c) Berechnen Sie die Koordinaten des Schnittpunkts S<sub>a</sub> von g<sub>a</sub> mit H. | ||
| + | |||
| + | [ Zur Kontrolle: S<sub>a</sub> = (a<sup>2</sup> + 3a / -3a / 8 - a<sup>2</sup>) ] | ||
| + | |||
| + | <div align="right"><i>'''3 BE'''</i></div> | ||
| + | <br> | ||
| + | :{{Lösung versteckt|[[Bild:Mainberger_Lea_2003_V_1c.jpg]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | d) Zeigen Sie, dass der Punkt S (-2 / 6 / 4) derjenige Punkt aus der Schar der Schnittpunkte S<sub>a</sub> ist, der die geringste Entfernung vom Ursprung hat. Geben Sie diese Entfernung an. | ||
| + | |||
| + | <div align="right"><i>'''9 BE'''</i></div> | ||
| + | <br> | ||
| + | :{{Lösung versteckt|[[Bild:Mainberger_Lea_2003_V_1d_1.jpg]][[Bild:Mainberger_Lea_2003_V_1d_2.jpg]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | e) Die Punkte S<sub>a</sub> bilden in H eine Kurve. Diese wird parallel zur | ||
| + | x<sub>3</sub>-Achse in die x<sub>1</sub>x<sub>2</sub>-Ebene projiziert; die Projektion heißt P. | ||
| + | Fertigen Sie eine Zeichnung von P in der x<sub>1</sub>x<sub>3</sub>-Ebene an. Um welchen Kurventyp handelt es sich bei P vermutlich? Überprüfen Sie Ihre Vermutung, indem Sie eine Koordinatengleichung von P aufstellen. | ||
| + | |||
| + | <div align="right"><i>'''8 BE'''</i></div> | ||
| + | <br> | ||
| + | :{{Lösung versteckt|[[Bild:Mainberger_Lea_2003_V_1e.jpg]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 2 | ||
| + | Ferner sind die Punkte A ( 1 / 6 / 1) und B (-2 / 9 / 1) gegeben. | ||
| + | |||
| + | |||
| + | a) Weisen Sie nach, dass sich die Punkte A und B zu einem regulären Sechseck ABCDEF mit dem Mittelpunkt S (-2 / 6 / 4) ergänzen lassen. | ||
| + | Ermitteln Sie die Koordinaten der Ergänzungspunkte C und D. | ||
| + | |||
| + | |||
| + | <div align="right"><i>'''5 BE'''</i></div> | ||
| + | <br> | ||
| + | :{{Lösung versteckt|[[Bild:Mainberger_Lea_2003_V_2a.jpg]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | b) Das Sechseck ABCDEF rotiert nun um die Achse AD.Beschreiben Sie das Aussehen des dabei entstehenden Rotationskörpers. Ermitteln Sie eine Gleichung der kleinsten Kugel, die den Rotationskörper enthält. | ||
| + | Liegt der Ursprung des Koordinatensystems innerhalb oder außerhalb dieses Rotationskörpers? Begründen Sie Ihre Antwort. | ||
| + | |||
| + | |||
| + | <div align="right"><i>'''6 BE'''</i></div> | ||
| + | <br> | ||
| + | :{{Lösung versteckt|[[Bild:Mainberger_Lea_2003_V_2b.jpg]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | </div> | ||
Aktuelle Version vom 22. April 2010, 17:46 Uhr
|
|
|
In einem kartesischen Koordinatensystem des
|
a) Zeigen Sie, dass keine der Geraden ga parallel und keine senkrecht zur Ebene H verläuft. 3 BE
b) Welche dieser Geraden schneidet H unter dem größten Winkel? Berechnen Sie diesen maximalen Winkel auf eine Dezimale genau. 6 BE
[ Zur Kontrolle: Sa = (a2 + 3a / -3a / 8 - a2) ] 3 BE
9 BE
8 BE
|
Ferner sind die Punkte A ( 1 / 6 / 1) und B (-2 / 9 / 1) gegeben.
5 BE
6 BE
|
 3 ist die
Ebene H: x1 + x2 + x3 - 8 = 0 , sowie die Schar von Geraden ga :
3 ist die
Ebene H: x1 + x2 + x3 - 8 = 0 , sowie die Schar von Geraden ga : 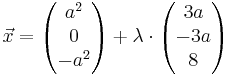 ,
, 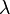 ∈
∈