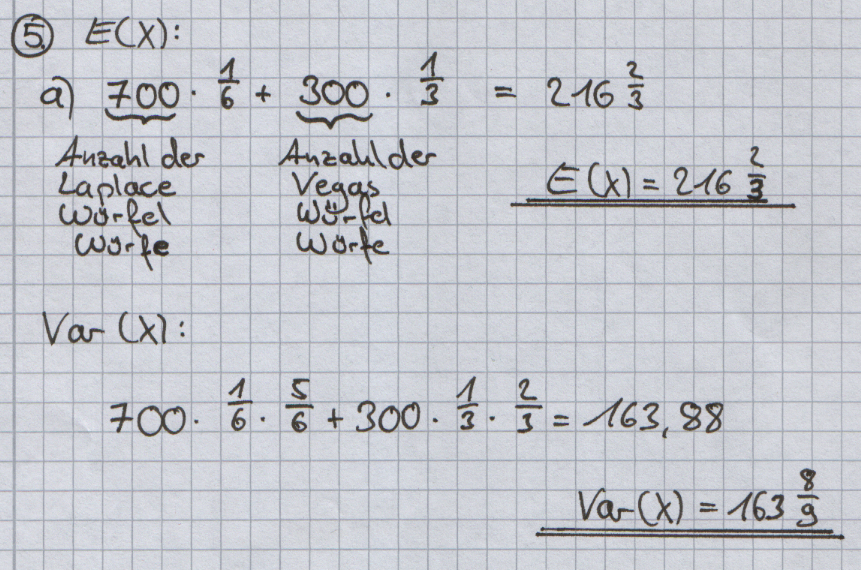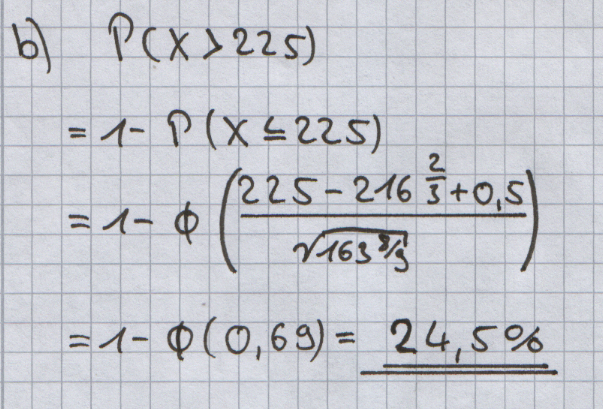2006 IV: Unterschied zwischen den Versionen
| (16 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
<center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung 2006'''</big></center> | <center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung 2006'''</big></center> | ||
| − | <center><big>''' | + | <center><big>'''Stochastik IV'''</big></center> |
| − | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID= | + | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=ff574c530ac05ed359667c29b75a15ff '''Download der Originalaufgaben: Abitur 2006 LK Mathematik Bayern'''] - [[Media:Burkard Christian_AbiM06_Lk.pdf|Lösung gesamt]]</center> |
| − | <center>Erarbeitet von | + | <center>Erarbeitet von Christian Burkard und Julius Schmidt</center> |
</td></tr></table></center> | </td></tr></table></center> | ||
| Zeile 24: | Zeile 24: | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| − | + | ||
Die Firma VEGAS hat ein neues Gesellschaftsspiel entwickelt, bei dem | Die Firma VEGAS hat ein neues Gesellschaftsspiel entwickelt, bei dem | ||
neben Laplace-Würfeln auch spezielle Vegas-Würfel verwendet werden, die | neben Laplace-Würfeln auch spezielle Vegas-Würfel verwendet werden, die | ||
sich äußerlich von den Laplace-Würfeln nicht unterscheiden. Die Vegas- | sich äußerlich von den Laplace-Würfeln nicht unterscheiden. Die Vegas- | ||
| − | Würfel zeigen die Augenzahl „6“ mit der erhöhten Wahrscheinlichkeit | + | Würfel zeigen die Augenzahl „6“ mit der erhöhten Wahrscheinlichkeit <math>\frac{1}{3}</math> , |
| − | 1 , | + | |
während die anderen Augenzahlen untereinander gleich wahrscheinlich sind. | während die anderen Augenzahlen untereinander gleich wahrscheinlich sind. | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
| + | Zeigen Sie, dass der Erwartungswert der Zufallsgröße „Augenzahl beim einmaligen Werfen eines Vegas-Würfels“ 4 ist. | ||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:1.jpg]] | ||
| + | }} | ||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 2 | ||
| + | Auf dem Tisch liegen ungeordnet drei Laplace-Würfel und ein Vegas-Würfel. Ein Spieler nimmt davon zufällig drei Würfel und wirft sie gleichzeitig. | ||
| + | Mit welcher Wahrscheinlichkeit erzielt er drei gleiche Augenzahlen, wenn er drei Laplace-Würfel genommen hat? Mit welcher Wahrschein-lichkeit erzielt er drei gleiche Augenzahlen, wenn er zwei Laplace-Würfel und den Vegas-Würfel genommen hat? | ||
| + | Welche Folgerung können Sie aus Ihren Ergebnissen bezüglich der stochastischen Abhängigkeit der Ereignisse „Er erzielt drei gleiche Augenzahlen“ und „Er nimmt drei Laplace-Würfel“ ziehen? | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| + | [[Bild:2.jpg]] | ||
| + | }} | ||
| + | </td></tr></table></center> | ||
| + | |||
| + | </div> | ||
| + | |||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 3 | ||
| + | Um bei einem Würfel festzustellen, ob es sich um einen Laplace- oder Vegas-Würfel handelt, wird er 100 mal geworfen. Ein Vegas-Würfel soll mit einer Wahrscheinlichkeit von mindestens 99 % als solcher eingestuft werden. | ||
| + | ;a) | ||
| + | Bestimmen Sie hierzu die Entscheidungsregel anhand der Anzahl der geworfenen Sechser so, dass möglichst auch ein Laplace-Würfel richtig eingestuft wird. | ||
| + | [Ergebnis: Entscheidung für Vegas-Würfel ab 23 geworfenen Sechsern] | ||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:jsucb_3a.jpg]] | ||
}} | }} | ||
| + | ;b) | ||
| + | Mit welcher Wahrscheinlichkeit wird bei dieser Entscheidungsregel ein Laplace-Würfel falsch eingestuft? | ||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:jsucb_3b.jpg]] | ||
| + | }} | ||
| + | </td></tr></table></center> | ||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | Eine Packung des Spiels enthält – ungeordnet und äußerlich nicht unter-scheidbar – 7 Laplace- und 3 Vegas-Würfel. | ||
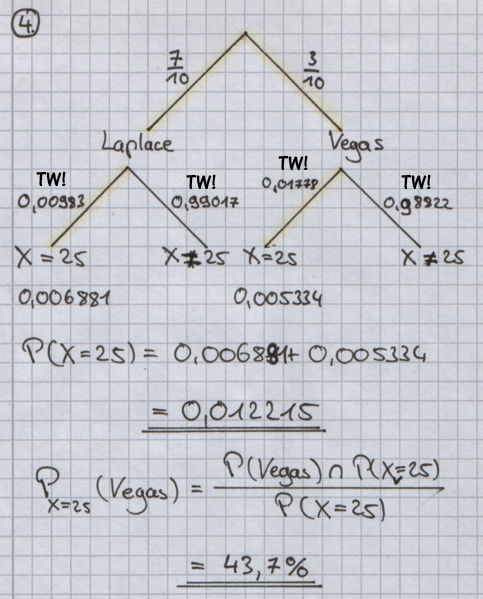
| + | ;Aufgabe 4 | ||
| + | Aus dieser Packung wird ein Würfel entnommen und 100-mal geworfen. Mit welcher Wahrschein¬lichkeit handelt es sich um einen Vegas-Würfel, wenn dabei 25-mal eine „6“ geworfen wird? | ||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:Burkard Christian_483px-4.jpg]] | ||
| + | }} | ||
</td></tr></table></center> | </td></tr></table></center> | ||
</div> | </div> | ||
| + | |||
<div style="padding:1px;background: #EEEEE6;border:0px groove;"> | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| Zeile 50: | Zeile 105: | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| − | ;Aufgabe 2 | + | ;Aufgabe 5 |
| + | Die 10 Würfel werden nun einzeln nacheinander aus der Packung ent-nommen und je 100-mal geworfen. | ||
| + | ;a) | ||
| + | Die Zufallsgröße X bezeichne die Anzahl der geworfenen Sechser unter den insgesamt 1000 durchzuführenden Würfen. Berechnen Sie Erwartungs¬wert und Varianz von X. | ||
| + | [Ergebnis: <math>E(X)=216\frac{2}{3}, Var(X) = 163\frac{8}{9}</math> ] | ||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:5a.jpg]] | ||
| + | }} | ||
| + | ;b) | ||
| + | Die Zufallsgröße X ist näherungsweise normalverteilt. Berechnen Sie mit Hilfe der Normalverteilung, mit welcher Wahrscheinlichkeit bei den 1000 Würfen mehr als 225-mal eine „6“ geworfen wird. | ||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:5b.jpg]] | ||
| + | }} | ||
| + | </td></tr></table></center> | ||
| + | </div> | ||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 6 | ||
| + | Bei einem Spiel werden jeweils 5 Würfel geworfen. Aus den Augen-zahlen – aufgefasst als Ziffern – werden möglichst große fünfstellige natürliche Zahlen gebildet, z. B. 43321, nicht jedoch 34312. | ||
| + | ;a) | ||
| + | Mit welcher Wahrscheinlichkeit erhält man eine Zahl größer als 50000, wenn es sich um 5 Laplace-Würfel handelt? | ||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:6a.jpg]] | ||
| + | }} | ||
| + | ;b) | ||
| + | Wie viele verschiedene natürliche Zahlen können nach dieser Spiel-regel gebildet werden? Wählen Sie aus den folgenden kombina-torischen „Modellen“ zunächst das für dieses Problem passende aus und bestimmen Sie dann mit dessen Hilfe die gesuchte Anzahl. | ||
| + | |||
| + | A) Anzahl der fünfstelligen Zahlen aus den Ziffern 1 bis 6 dividiert durch die Zahl der Permutationen von 5 Elementen | ||
| + | |||
| + | B) Zahl der möglichen Verteilungen von 5 Kugeln auf 6 Urnen, wobei es nur auf die jeweilige Anzahl der Kugeln in den Urnen ankommt | ||
| + | |||
| + | C) Zahl der möglichen Verteilungen von 6 Kugeln auf 5 Urnen, wobei es nur auf die jeweilige Anzahl der Kugeln in den Urnen ankommt | ||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:6b.jpg]] | ||
| + | }} | ||
</td></tr></table></center> | </td></tr></table></center> | ||
</div> | </div> | ||
Aktuelle Version vom 11. April 2010, 15:51 Uhr
|
|
|
Zeigen Sie, dass der Erwartungswert der Zufallsgröße „Augenzahl beim einmaligen Werfen eines Vegas-Würfels“ 4 ist. |
Auf dem Tisch liegen ungeordnet drei Laplace-Würfel und ein Vegas-Würfel. Ein Spieler nimmt davon zufällig drei Würfel und wirft sie gleichzeitig. Mit welcher Wahrscheinlichkeit erzielt er drei gleiche Augenzahlen, wenn er drei Laplace-Würfel genommen hat? Mit welcher Wahrschein-lichkeit erzielt er drei gleiche Augenzahlen, wenn er zwei Laplace-Würfel und den Vegas-Würfel genommen hat? Welche Folgerung können Sie aus Ihren Ergebnissen bezüglich der stochastischen Abhängigkeit der Ereignisse „Er erzielt drei gleiche Augenzahlen“ und „Er nimmt drei Laplace-Würfel“ ziehen? |
Um bei einem Würfel festzustellen, ob es sich um einen Laplace- oder Vegas-Würfel handelt, wird er 100 mal geworfen. Ein Vegas-Würfel soll mit einer Wahrscheinlichkeit von mindestens 99 % als solcher eingestuft werden.
Bestimmen Sie hierzu die Entscheidungsregel anhand der Anzahl der geworfenen Sechser so, dass möglichst auch ein Laplace-Würfel richtig eingestuft wird. [Ergebnis: Entscheidung für Vegas-Würfel ab 23 geworfenen Sechsern]
Mit welcher Wahrscheinlichkeit wird bei dieser Entscheidungsregel ein Laplace-Würfel falsch eingestuft? |
|
Eine Packung des Spiels enthält – ungeordnet und äußerlich nicht unter-scheidbar – 7 Laplace- und 3 Vegas-Würfel.
Aus dieser Packung wird ein Würfel entnommen und 100-mal geworfen. Mit welcher Wahrschein¬lichkeit handelt es sich um einen Vegas-Würfel, wenn dabei 25-mal eine „6“ geworfen wird? |
Die 10 Würfel werden nun einzeln nacheinander aus der Packung ent-nommen und je 100-mal geworfen.
Die Zufallsgröße X bezeichne die Anzahl der geworfenen Sechser unter den insgesamt 1000 durchzuführenden Würfen. Berechnen Sie Erwartungs¬wert und Varianz von X.
[Ergebnis:
Die Zufallsgröße X ist näherungsweise normalverteilt. Berechnen Sie mit Hilfe der Normalverteilung, mit welcher Wahrscheinlichkeit bei den 1000 Würfen mehr als 225-mal eine „6“ geworfen wird. |
Bei einem Spiel werden jeweils 5 Würfel geworfen. Aus den Augen-zahlen – aufgefasst als Ziffern – werden möglichst große fünfstellige natürliche Zahlen gebildet, z. B. 43321, nicht jedoch 34312.
Mit welcher Wahrscheinlichkeit erhält man eine Zahl größer als 50000, wenn es sich um 5 Laplace-Würfel handelt?
Wie viele verschiedene natürliche Zahlen können nach dieser Spiel-regel gebildet werden? Wählen Sie aus den folgenden kombina-torischen „Modellen“ zunächst das für dieses Problem passende aus und bestimmen Sie dann mit dessen Hilfe die gesuchte Anzahl. A) Anzahl der fünfstelligen Zahlen aus den Ziffern 1 bis 6 dividiert durch die Zahl der Permutationen von 5 Elementen B) Zahl der möglichen Verteilungen von 5 Kugeln auf 6 Urnen, wobei es nur auf die jeweilige Anzahl der Kugeln in den Urnen ankommt C) Zahl der möglichen Verteilungen von 6 Kugeln auf 5 Urnen, wobei es nur auf die jeweilige Anzahl der Kugeln in den Urnen ankommt |
 ,
während die anderen Augenzahlen untereinander gleich wahrscheinlich sind.
,
während die anderen Augenzahlen untereinander gleich wahrscheinlich sind.



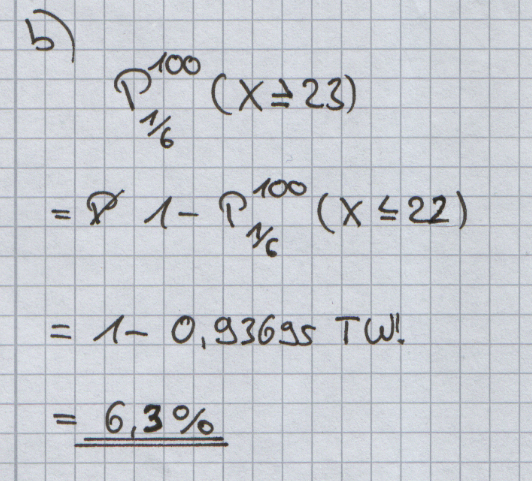
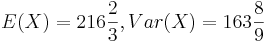 ]
]