Verfahren Extremwertbeweis durch 2. Ableitung: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: '''Extremwertbeweis durch die 2. Ableitung:''' Ein Extremwertbeweis ist neben den beiden anderen genannten Möglichkeiten ebenfalls mit Hilfe des Verfahrens durch die...) |
|||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
'''Extremwertbeweis durch die 2. Ableitung:''' | '''Extremwertbeweis durch die 2. Ableitung:''' | ||
| − | |||
Ein Extremwertbeweis ist neben den beiden anderen genannten Möglichkeiten ebenfalls mit Hilfe des Verfahrens durch die 2. Ableitung möglich. Hierzu sind drei Schritte nötig, welche sich aus dem Suchen eines möglichen Extrempunktes, dem Bilden der 2. Ableitung und dem Beweis der Existenz der Extremstelle zusammensetzt. Zunächst muss die Nullstelle der 1. Ableitung gesucht werden. Anschließend wird die 2. Ableitung gebildet und zu guter Letzt der x-Wert der möglichen Extremstelle in die 2. Ableitung eingesetzt. Hierbei wird darauf geachtet, ob die 2. Ableitung größer oder kleiner 0 ist. Falls sie größer 0 ist, tritt an dieser Stelle ein Minimum auf, falls sie kleiner 0 ist, tritt an dieser Stelle ein Maximum auf. | Ein Extremwertbeweis ist neben den beiden anderen genannten Möglichkeiten ebenfalls mit Hilfe des Verfahrens durch die 2. Ableitung möglich. Hierzu sind drei Schritte nötig, welche sich aus dem Suchen eines möglichen Extrempunktes, dem Bilden der 2. Ableitung und dem Beweis der Existenz der Extremstelle zusammensetzt. Zunächst muss die Nullstelle der 1. Ableitung gesucht werden. Anschließend wird die 2. Ableitung gebildet und zu guter Letzt der x-Wert der möglichen Extremstelle in die 2. Ableitung eingesetzt. Hierbei wird darauf geachtet, ob die 2. Ableitung größer oder kleiner 0 ist. Falls sie größer 0 ist, tritt an dieser Stelle ein Minimum auf, falls sie kleiner 0 ist, tritt an dieser Stelle ein Maximum auf. | ||
| Zeile 26: | Zeile 25: | ||
Daran dass die 2. Ableitung an der der Stelle des möglichen Extremwertes größer 0 ist, erkennt man eindeutig, dass es sich hierbei um ein Minimum der Funktion handelt. Ob dies ein lokales Minimum ist oder ein Minimum für die ganze Funktion ist, kann allerdings nur durch die Überprüfung der Grenzwerte festgestellt werden. | Daran dass die 2. Ableitung an der der Stelle des möglichen Extremwertes größer 0 ist, erkennt man eindeutig, dass es sich hierbei um ein Minimum der Funktion handelt. Ob dies ein lokales Minimum ist oder ein Minimum für die ganze Funktion ist, kann allerdings nur durch die Überprüfung der Grenzwerte festgestellt werden. | ||
| + | |||
| + | Hinweis: | ||
| + | |||
| + | {{Lösung versteckt| | ||
| + | Falls die 2. Ableitung am Punkt des möglichen Extrempunktes ebenfalls 0 ist, kann trotzdem ein Extrempunkt vorliegen. Wenn dieser Fall eintritt, bedeutet das, dass der mögliche Extrempunkt ebenfalls ein Wendepunkt wäre. Dieser kann mit den im späteren Verlauf genannten Methoden nachgewiesen werden. | ||
| + | |||
| + | Wenn es nun keinen Wendepunkt an dieser Stelle gibt, ist an dieser Stelle auch kein Extrempunkt.<br /> | ||
| + | Falls an dieser Stelle ein Wendepunkt auftritt, ist es ebenfalls ein Extrempunkt. Dieser besondere Punkt wird dann Terrassenpunkt genannt. | ||
| + | }} | ||
| + | |||
| + | |||
| + | <br /> | ||
| + | [[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung b)|Hier geht's zurück zur Lösung b)]] | ||
Aktuelle Version vom 29. Januar 2010, 10:52 Uhr
Extremwertbeweis durch die 2. Ableitung:
Ein Extremwertbeweis ist neben den beiden anderen genannten Möglichkeiten ebenfalls mit Hilfe des Verfahrens durch die 2. Ableitung möglich. Hierzu sind drei Schritte nötig, welche sich aus dem Suchen eines möglichen Extrempunktes, dem Bilden der 2. Ableitung und dem Beweis der Existenz der Extremstelle zusammensetzt. Zunächst muss die Nullstelle der 1. Ableitung gesucht werden. Anschließend wird die 2. Ableitung gebildet und zu guter Letzt der x-Wert der möglichen Extremstelle in die 2. Ableitung eingesetzt. Hierbei wird darauf geachtet, ob die 2. Ableitung größer oder kleiner 0 ist. Falls sie größer 0 ist, tritt an dieser Stelle ein Minimum auf, falls sie kleiner 0 ist, tritt an dieser Stelle ein Maximum auf.
Da bei unserer gegebenen Funktion keine Extremstellen auftreten, werde ich an einem selbstgewählten Beispiel erklären, wie genau dieses Verfahren funktioniert.
Beispielaufgabe:
Bestimmung der Nullstelle der 1. Ableitung:
Beweis für Extrempunkt:
Daran dass die 2. Ableitung an der der Stelle des möglichen Extremwertes größer 0 ist, erkennt man eindeutig, dass es sich hierbei um ein Minimum der Funktion handelt. Ob dies ein lokales Minimum ist oder ein Minimum für die ganze Funktion ist, kann allerdings nur durch die Überprüfung der Grenzwerte festgestellt werden.
Hinweis:
Falls die 2. Ableitung am Punkt des möglichen Extrempunktes ebenfalls 0 ist, kann trotzdem ein Extrempunkt vorliegen. Wenn dieser Fall eintritt, bedeutet das, dass der mögliche Extrempunkt ebenfalls ein Wendepunkt wäre. Dieser kann mit den im späteren Verlauf genannten Methoden nachgewiesen werden.
Wenn es nun keinen Wendepunkt an dieser Stelle gibt, ist an dieser Stelle auch kein Extrempunkt.
Falls an dieser Stelle ein Wendepunkt auftritt, ist es ebenfalls ein Extrempunkt. Dieser besondere Punkt wird dann Terrassenpunkt genannt.
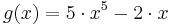
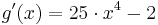
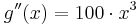
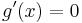
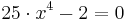
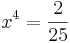
![x = \sqrt[4]{\frac {2}{25}}](/images/math/2/d/f/2df8033ed462bb75fb46d671d2698434.png)
![g''(\sqrt[4]{\frac {2}{25}}) = 100\cdot (\sqrt[4]{\frac {2}{25}})^{3} > 0](/images/math/8/a/7/8a748d3391bd1ebec89e17145ecee315.png)

