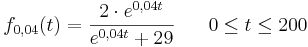Lösung d): Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(→‎Erläutern Sie die Grenzen dieser mathematischen Modellbildung)
(→‎Berechnen Sie, wann die Wachstumsgeschwindigkeit einer Sonnenblumenpflanze am größten ist)
 
Zeile 35: Zeile 35:
  
 
<br />
 
<br />
−
Daraus folgt die Bedingung: <math>f''_{0,04} (t) = 0\;</math>
+
Im nachfolgenden Bild lässt sich die 1. Ableitung und 2. Ableitung der Funktion f erkennen. Anhand des Graphen der 1. Ableitung (rot) erkennt man sehr leicht, dass es ein Maximum der Wachstumsgeschwindigkeit gibt. Dieses tritt ja bekanntlicherweise auf, wenn die 2. Ableitung gleich 0 ist, was in dem blauen Graphen erkennbar ist, welcher die 2. Ableitung darstellt.
  
−
<br />
 
−
[[Bild:Graph-facharbeit8.png|450px|Graph der 1. Ableitung (rot) und 2. Ableitung (blau)]]
 
  
 +
[[Bild:Graph-facharbeit8.png|450px]]
 +
 +
 +
Daraus folgt die Bedingung für ein Wachstumsgeschwindigkeitsmaximum: <math>f''_{0,04} (t) = 0\;</math>
 
<br />
 
<br />
 
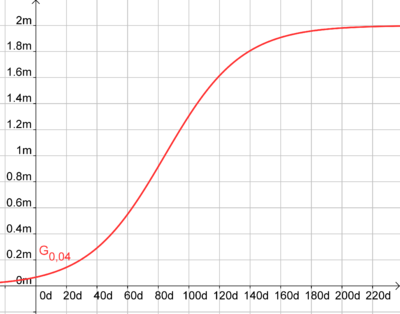
Dies gilt für den Wendepunkt, der bereits in [[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung b)| Teilaufgabe b)]] berechnet und liegt bei <math>t = \frac {ln29} {0,04} = 84,2</math>
 
Dies gilt für den Wendepunkt, der bereits in [[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung b)| Teilaufgabe b)]] berechnet und liegt bei <math>t = \frac {ln29} {0,04} = 84,2</math>

Aktuelle Version vom 28. Januar 2010, 23:33 Uhr

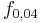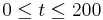Durch die Funktion f_{0,04}\; für 0\leq t\leq 200 (t in Tagen) kann das Wachstum von Sonnenblumen beschrieben werden, wobei 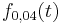f_{0,04} (t)\; die Höhe (in m) der Pflanzen zur Zeit t bedeutet.

f_{0,04} (t) = \frac {2\cdot e^{0,04t}} {e^{0,04t} + 29}\;\;\;\;\;\;0\leq t\leq 200

Berechnen Sie die Höhe einer Sonnenblumenpflanze nach 10, 50 und 150 Tagen


Graph-facharbeit7.png

Da der Graph der Funktion das Wachstum einer Sonnenblumenpflanze in m beschreibt, wobei die Variable t die Zeit darstellt, muss man lediglich t in die Gleichung einsetzen und erfährt die Höhe in m nach der verstrichenen Zeit t.

Höhe nach 10 Tagen:

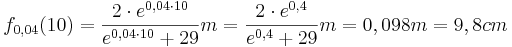
f_{0,04} (10) = \frac {2\cdot e^{0,04\cdot 10}} {e^{0,04\cdot 10} + 29} m = \frac {2\cdot e^{0,4}} {e^{0,4} + 29} m = 0,098m = 9,8cm

Höhe nach 50 Tagen:

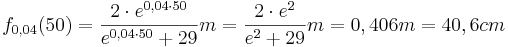
f_{0,04} (50) = \frac {2\cdot e^{0,04\cdot 50}} {e^{0,04\cdot 50} + 29} m = \frac {2\cdot e^{2}} {e^{2} + 29} m = 0,406m = 40,6cm

Höhe nach 150 Tagen:

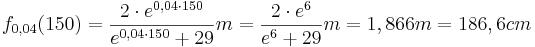
f_{0,04} (150) = \frac {2\cdot e^{0,04\cdot 150}} {e^{0,04\cdot 150} + 29} m = \frac {2\cdot e^{6}} {e^{6} + 29} m = 1,866m = 186,6cm


Berechnen Sie, wann die Wachstumsgeschwindigkeit einer Sonnenblumenpflanze am größten ist


Graph der Funktion (rot) und der Tangente im Wendepunkt (blau)
  • Die Funktion 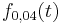f_{0,04} (t)\; beschreibt die Höhe der Sonnenblumenpflanze in Abhängigkeit der Zeit t (hier rot zu erkennen)
  • Die 1. Ableitung der Funktion 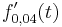f'_{0,04} (t)\; beschreibt die Wachstumsgeschwindigkeit in Abhängigkeit der Zeit t (hier blau zu erkennen)


Wenn die Steigung der 1. Ableitung gleich 0 ist und an dieser Stelle ein Maximum ist, ist die Wachstumsgeschwindigkeit am größten.


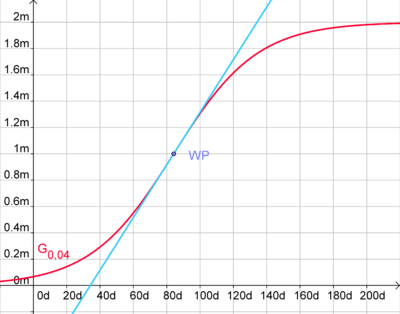
Im nachfolgenden Bild lässt sich die 1. Ableitung und 2. Ableitung der Funktion f erkennen. Anhand des Graphen der 1. Ableitung (rot) erkennt man sehr leicht, dass es ein Maximum der Wachstumsgeschwindigkeit gibt. Dieses tritt ja bekanntlicherweise auf, wenn die 2. Ableitung gleich 0 ist, was in dem blauen Graphen erkennbar ist, welcher die 2. Ableitung darstellt.


Graph-facharbeit8.png


Daraus folgt die Bedingung für ein Wachstumsgeschwindigkeitsmaximum: 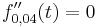f''_{0,04} (t) = 0\;
Dies gilt für den Wendepunkt, der bereits in Teilaufgabe b) berechnet und liegt bei 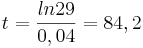t = \frac {ln29} {0,04} = 84,2

Erläutern Sie die Grenzen dieser mathematischen Modellbildung

Sonnenblumen auf einem Feld

Diese Betrachtung des Pflanzenwachstums ist eine mathematische Modellvorstellung und somit eine reine theoretische Modellvorstellung. Aufgrund dessen gibt es bei dieser Art der Vorstellung gewisse Grenzen, die man in jedem Fall zu beachten hat und nicht vernachlässigen darf, damit es nicht zu Misvertständnissen kommt. Im Nachfolgenden werden nun einige Beispiele für diese Grenzen gegeben.


Eine Grenze die man in jedem Fall nennen muss, ist diese, dass diese mathematische Funktion zwar den Wachstum einer Sonnenblumenpflanze beschreibt, jedoch ist dies nur ein Mittelwert. Dies bedeutet, dass man keine wirkliche Aussage darüber machen kann, wie eine einzelne Pflanze wächst.

Dies bedeutet, dass man in einem Testversuch mit drei Pflanzen möglicherweise drei verschiedene Höhen der Sonnenblumenpflanzen bekommt. Wenn man jedoch einen Test mit einer großen Anzahl an Sonnenblumen durchführt, wird mit sehr großer Wahrscheinlichkeit die gemittelte Kurve des Wachstums durch die Funktion 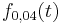f_{0,04} (t)\; beschrieben.


Eine weitere Grenze dieser mathematischen Modellvorstellung ist, dass das Sonnenblumenwachstum von einigen Faktoren beeinflusst wird, welche nicht überall auf der Welt gleich sind. Sonnenblumen benötigen beispielsweise sehr viel Licht und Wärme, was dazu führt, dass in wärmeren Gebieten die Blumen schneller wachsen und kälteren weniger schnell und ebenfalls weniger hoch.

Dies bedeutet, dass die Wachstumskurve in anderen Gebieten der Erde deutlich anders verlaufen kann, einen anderen Grenzwert gegen 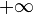+ \infty haben kann oder das Wachstum einfach langsamer bzw. schneller verlaufen kann.



Zurück zur Aufgabe

Von „http://rmg.zum.de/index.php?title=Facharbeit_Mathematik_Straßheimer/Die_Aufgabe/Lösung_d)&oldid=28569“