Teilaufgabe a: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
 
(3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 2: Zeile 2:
  
  
−
:1.Untersuchen Sie den Graphen von <math>f_a\,</math> auf:
+
:1. Untersuchen Sie den Graphen von <math>f_a\,</math> auf:
 
::*Schnittpunkte mit den Koordinatenachsen,<br />[[Facharbeit Andre Etzel/Teilaufgabe a/Lösung: Schnittpunkte mit den Koordinatenachsen|Lösung: Schnittpunkte mit den Koordinatenachsen]]
 
::*Schnittpunkte mit den Koordinatenachsen,<br />[[Facharbeit Andre Etzel/Teilaufgabe a/Lösung: Schnittpunkte mit den Koordinatenachsen|Lösung: Schnittpunkte mit den Koordinatenachsen]]
 
::*lokale Extrempunkte und<br /> [[Facharbeit Andre Etzel/Teilaufgabe a/Lösung: lokale Extrempunkte|Lösung: lokale Extrempunkte]]
 
::*lokale Extrempunkte und<br /> [[Facharbeit Andre Etzel/Teilaufgabe a/Lösung: lokale Extrempunkte|Lösung: lokale Extrempunkte]]
Zeile 10: Zeile 10:
  
  
−
:2.Alle Extrempunkte liegen auf dem Graphen einer Funktion h. Geben Sie eine Funktionsgleichung von h an!
+
:2. Alle Extrempunkte liegen auf dem Graphen einer Funktion h. Geben Sie eine Funktionsgleichung von h an!
  
 
{{Lösung versteckt|
 
{{Lösung versteckt|
Zeile 17: Zeile 17:
 
<math>\rightarrow H ( x ) = e</math><br />
 
<math>\rightarrow H ( x ) = e</math><br />
  
−
Alle Extrempunkte für <math>a\in R</math> befinde sich auf einer Parallelen zur x-Achse mit <math>y=e\;</math>.<br /> Das heißt, dass alle Extrempunkte auf dem Graphen der Funktion <math>H ( x ) = e\;</math> liegen.  
+
Alle Extrempunkte für <math>a\in R</math> befinden sich auf einer Parallelen zur x-Achse mit <math>y=e\;</math>.<br /> Das heißt, dass alle Extrempunkte auf dem Graphen der Funktion <math>H ( x ) = e\;</math> liegen.  
  
−
<ggb_applet width="773" height="460"  version="3.2" ggbBase64="UEsDBBQACAAIAMGmNzwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1szVbfb9s2EH5u/wpCT0m72JJspwlgp9i6hxVI2wdvfdhDAUo6WVwoUSCpRM5f3+ORtB0364IuGPZgSLw734/vvjtq+XZsJbsFbYTqVkk2SRMGXakq0W1WyWDrs4vk7dXL5QbUBgrNWa10y+0qmU3yxMkHcfXyxdI06o5xSSafBdytEqsHSJjpNfDKNADWi2suDcr5MAopuN5+Kv6C0pq9wvt43/WDjU7KtroWJh6nFK+Xwv4qbkUFmklVrpLzBWaOb59BW1FyuUrmqZfkWNb5QyWKZk7bKC3uVWed+d55jRLGjLgH/GfuZMsp1bmEoZSiErxzxVAeaMTYnahsgymkb9AliE2Duc4XF95bqZSu1ltjoWXjn6DVKsmzhcN5608zfzKYFwZcpKQ6PJEbuF2DtdgVw/gIJmKz0aLagecO780vSu5FvRKdfcd7O2jq6CyI1nbr/GMo7fL9udtICLIMEW+gvCnUuPYYzLzr37c9/YXyKTbvlFSaaSxnsUCD8Cz8k2xcojurlGxSsgg+nNOdPrvMyYKehX+SlRSdTy0UnsWqszSGEYY5gUMRiRixkbwAbGzChk7Y63hAAtzsK3X2H4e2wAE4pMDOZfZMLpfTI+4sb0B3ID1DOmzsoAbDbh0TfesojwpK0eLRKwIg3DXrD0zASyvYaIh5+/HxcJE2PWThkXg5jUm4HAzmWlpcA1iPdbW4MbU4Iu6t4tZJ3AxIaAEHxBIbuqEFLcodMjxx0TDEEAJlkcC0IhSN+xGae9hR/Td8wcXQNxzfJllgBd/i6B+WSN4+qCoGDmEl7YhW4HY7o0Fr+YiD5d54YZQcLKxLBLC7ViW3tAV9dmGqs5QmcnQrg0YzzmgtRtgP2uOrZM9d2yBJOjDGtTGAF/nbYY8JeFwSva8RNyeA51+0ZT3WTEO8IwiyynfjH/sCx33JJ2+yi/zC/eaLy3S+eKRLobT/ok0EppccTGG8JR4qHlQ94g1j3OUV06zxAhsRxfpkPGUrdjKyM8ZP2SsGX044e83ySYqS8TRh029Qq4eOJiDZO3tyF5+L3+l3gftU1wasY+MlUfHsfP4orOmT+fd9NJuAZuPRhCeh1vzfUHt+XH4LuBClcMf9xOA0/p0u2MeACoqdi38LAF24PwoB3QjGMSkPa+3blcDuDxa4/25wHzzkZnYM0vTwDqFvpvDNePUVUEsHCBT7mod+AwAAZQoAAFBLAQIUABQACAAIAMGmNzwU+5qHfgMAAGUKAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAuAMAAAAA" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" />}}<br />
+
<ggb_applet width="660" height="396"  version="3.2" ggbBase64="UEsDBBQACAAIAFabOjwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1svVZLc+Q0ED6zv0LlUwJkxvY8UzWTLVg4bFWAw8AeOFAl2z0eEdkykpx48uvplmR7MsmygQVSlbLd3dOPr79uafO2qyS7B22EqrdRMokjBnWuClGX26i1+6t19PbmzaYEVUKmOdsrXXG7jWaTNCJ5K27efLExB/XAuHQmHwQ8bKM9lwYiZhoNvDAHAPtEzttOSMH18afsd8itGRXeyfu6aTGK1S3K8qq4Fab/nLqAjRT2O3EvCtBMqnwbLReYOr59AG1FzuU2msdekm6j9EyJohlpD0qLR1VbMh+d71HCmBGPgIikJNtMXaEbaHMpCsFrKsblgUaMPYjCHjCFJbkEUR4IoOu595YrpYvd0VioWPcraIXprNYTzG74SyJ2DJrFcrI60cQLxBATxkwWMTXnGL6W8WS1Xs6W8Xw1S+N1vPLB4H4H1mLzDOMdmB7BUotigJg+3ptvlRxFjRK1fccb22rX+FkQ7eyRgmFcTVV9U5cSggxzzg+Q32Wq23mkZt71z8fG/cTlk5XvlFSaaSoNaynDM/NPZ0OJDlaxs4mdRfBBTgd9cp06C/fM/NNZSVH71ELhSV91EvdhhGEkQOfE1x4byTPA9kesrYW97T+QJndjpWT/Y1tlOCenRBlcJv+Sy830jGGbO9A1SM+jGhvbqtawe+Krb53Lo4BcVPjpFQEQTs36BRPw0gJKDX3efsg8XE4bn3L1TLyZ9klQDgZzzS1uC6zHUi00zBYHid4KbklCkyKhAhwj69hQtxVokQ/I8IiiYYg2BKLFMx02iXJL4QzNEXZUf4QvuD6aA8e3SRJYwY+4IE5LdN5+UEUfOISVbpNUApfg1YIGreIdzhy98cwo2VrY5Qhgfatybt2y9NmF2U9iN54dLRY3p/3A7kUH46C9vHBG7toDkqQGY6iNAbyevzX22AGPq6TxNeJ+BfD8621ZgzW7IR4Igqzy3fhkX+C8L+lklazTNf3PF9fxfPFCl0Jp/0ebHJhecjKF/VnyVPGk6g7PIUNnXJ/mHs+5DlHcX3SXbMsuOnbF+CX7ksFvF5x9xdJJjJLuMmLTZ6jt29pNQDQ6e3UX/y6/+635HLr4ldDFr+bYXyOWBcSOCBe8BAtFiEbr/wySUy6l8fyfQ+K2naGZ7UfW3X8ecQV8hPevqgf+qL2N8cseUZMiF/bTEH8fIHYMxFy+ZnDZO3fn8UuwB8Xg4rMhJcZ9PqRpgPQ5kgTwsO/9NYNuUc7N7Byk6emR4y5i4SZ68ydQSwcIZxEcsK0DAAC7CgAAUEsBAhQAFAAIAAgAVps6PGcRHLCtAwAAuwoAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAADnAwAAAAA=" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" />}}<br />
  
−
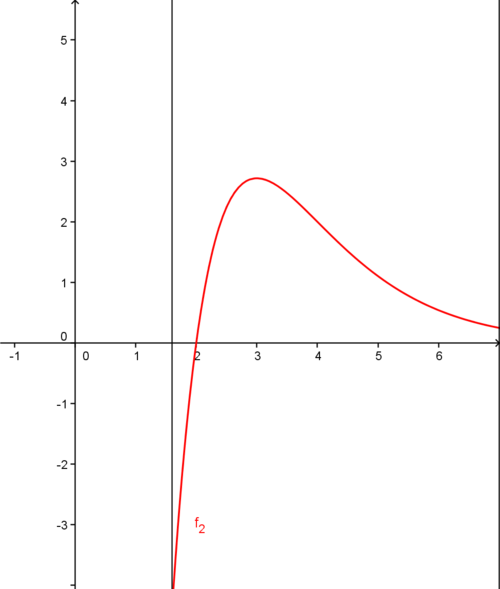
:3.Skizzieren Sie den Graphen der Funktion <math>f_2\,</math> für <math>1,6 \le  x  \le 7</math>!
+
:3. Skizzieren Sie den Graphen der Funktion <math>f_2\,</math> für <math>1,6 \le  x  \le 7</math>!
 
{{Lösung versteckt|
 
{{Lösung versteckt|
 
Graph der Funktion <math>f_2\,</math> für <math>1,6 \le  x  \le 7</math>
 
Graph der Funktion <math>f_2\,</math> für <math>1,6 \le  x  \le 7</math>

Aktuelle Version vom 26. Januar 2010, 19:28 Uhr

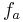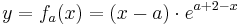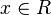Für jede reelle Zahl a sei eine Funktion f_a\, durch y = f_a (x) = ( x - a )\cdot e^{a+2-x} mit x\in R gegeben.


1. Untersuchen Sie den Graphen von 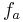f_a\, auf:
Bestimmen Sie gegebenenfalls deren Koordinaten!


2. Alle Extrempunkte liegen auf dem Graphen einer Funktion h. Geben Sie eine Funktionsgleichung von h an!

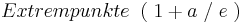
Extrempunkte\; \;(\; 1 + a \;/\; e\; )\;

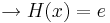
\rightarrow H ( x ) = e

Alle Extrempunkte für 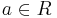a\in R befinden sich auf einer Parallelen zur x-Achse mit y=e\;.
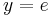Das heißt, dass alle Extrempunkte auf dem Graphen der Funktion 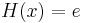H ( x ) = e\; liegen.


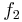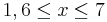3. Skizzieren Sie den Graphen der Funktion f_2\, für 1,6 \le x \le 7!

Graph der Funktion f_2\, für 1,6 \le x \le 7

Graph f 2.png


Von „http://rmg.zum.de/index.php?title=Facharbeit_Andre_Etzel/Teilaufgabe_a&oldid=28241“