LK Mathematik Abitur NRW 2007: Unterschied zwischen den Versionen
K |
|||
| (5 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | == | + | <center> |
| + | {|width=90%| style="background-color:#F5F5F5; border: 1px solid #63B8FF; padding:0.5em" | ||
| + | | valign="top" | | ||
| + | ''Bearbeitet wird eine Abituraufgabe von 2007 aus Nordrhein - Westfalen. Zu der Aufgabe sind auf der nächsten Seite einige Aufgaben gestellt, welche es zu bearbeiten gilt. Die interaktive Bearbeitung der Aufgabe ist so aufgebaut, dass zu Beginn nochmals erläutert wird was genau errechnet werden soll und wie die jeweilige Aufgabe zu berechnen ist. | ||
| + | |||
| + | Des Weiteren findest du neben den Aufgaben viele Veranschaulichungen durch Graphen in GeogebraApplets, von denen du manche auch durch einen Schieberegler verändern kannst. Dies ist vor allem für diejenigen nützlich, die sich die Lösungswege schwerer erschließen können und dadurch eine kleine Hilfestellung bekommen. | ||
| + | |||
| + | |||
| + | :Nun wünsche ich dir noch viel Spaß beim Bearbeiten der interaktiven Aufgabe. | ||
| + | |||
| + | :Und hier gehts auch schon zur [[Facharbeitsaufgabe|Wasserstandsaufgabe]]! | ||
| + | |} | ||
| + | </center> | ||
| + | <big>'''Aufgabenstellung:'''<ref>[http://www.standardsicherung.nrw.de/abitur-gost/getfile.php?file=910 Angabe als pdf Datei]</ref> | ||
| + | </big> | ||
| + | |||
[[Bild:Eilif_Peterssen-_Sevilosen.jpg|250px|right]] | [[Bild:Eilif_Peterssen-_Sevilosen.jpg|250px|right]] | ||
| − | |||
| − | + | Um die Wasserstände eines Flusses vorherzusagen, kann man versuchen, die Durchflussgeschwindigkeit | |
| + | des Wassers an einer bestimmten Stelle des Flusses mit Hilfe geeigneter | ||
| + | Funktionen zu beschreiben. | ||
| + | Solche näherungsweise Beschreibungen der Durchflussgeschwindigkeiten seien z. B. gegeben | ||
| + | durch die Funktionenschar <math>f_a (t) = \frac{1}{4}t^3 - a t^2 + a^2 t</math>, mit a > 0 . | ||
| + | |||
| + | Dabei gibt <math>f_a (t)</math> die Durchflussgeschwindigkeit in <math>10^6 \frac{m^3}{Monat}</math> (Millionen Kubikmeter pro | ||
| + | Monat) und t die verstrichene Zeit in Monaten seit Beginn der Vorhersage <math>t = 0</math> an. | ||
| + | Die Funktionen <math>f_a</math> berücksichtigen, dass es sich um einen Fluss handelt, der zeitweise | ||
| + | austrocknet. | ||
| + | |||
| + | |||
| − | + | :#[[LK Mathematik Abitur NRW 2007/Nullstellen|Berechnung der Zeitpunkte, in denen der Fluss austrocknet]] | |
| + | :#[[LK Mathematik Abitur NRW 2007/Extremwerte|Bestimmung der maximalen und minimalen Volumina]] | ||
| + | :#[[LK Mathematik Abitur NRW 2007/Wendepunkt|Bestimmung der größten Senkung der Durchflussgeschwindigkeit]] | ||
| + | :#[[LK Mathematik Abitur NRW 2007/Theoretische Überlegungen|Theoretische Fragen zur Wasserstandsaufgabe]] | ||
| + | :#[[LK Mathematik Abitur NRW 2007/Integralberechnung|Berechnung des Wasservolumens in den ersten sechs Monaten]] | ||
| + | :#[[LK Mathematik Abitur NRW 2007/Flächengleichheit|Volumengleicheit zweier verschiedener Funktionen bis zum Zeitpunkt t<sub>0</sub>]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <big>'''Internetquellen'''</big> | |
| + | :<references/> | ||
Aktuelle Version vom 6. Februar 2011, 15:52 Uhr
|
Bearbeitet wird eine Abituraufgabe von 2007 aus Nordrhein - Westfalen. Zu der Aufgabe sind auf der nächsten Seite einige Aufgaben gestellt, welche es zu bearbeiten gilt. Die interaktive Bearbeitung der Aufgabe ist so aufgebaut, dass zu Beginn nochmals erläutert wird was genau errechnet werden soll und wie die jeweilige Aufgabe zu berechnen ist. Des Weiteren findest du neben den Aufgaben viele Veranschaulichungen durch Graphen in GeogebraApplets, von denen du manche auch durch einen Schieberegler verändern kannst. Dies ist vor allem für diejenigen nützlich, die sich die Lösungswege schwerer erschließen können und dadurch eine kleine Hilfestellung bekommen.
|
Aufgabenstellung:[1]
Um die Wasserstände eines Flusses vorherzusagen, kann man versuchen, die Durchflussgeschwindigkeit
des Wassers an einer bestimmten Stelle des Flusses mit Hilfe geeigneter
Funktionen zu beschreiben.
Solche näherungsweise Beschreibungen der Durchflussgeschwindigkeiten seien z. B. gegeben
durch die Funktionenschar 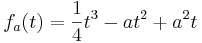 , mit a > 0 .
, mit a > 0 .
Dabei gibt 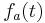 die Durchflussgeschwindigkeit in
die Durchflussgeschwindigkeit in 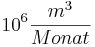 (Millionen Kubikmeter pro
Monat) und t die verstrichene Zeit in Monaten seit Beginn der Vorhersage
(Millionen Kubikmeter pro
Monat) und t die verstrichene Zeit in Monaten seit Beginn der Vorhersage 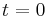 an.
Die Funktionen
an.
Die Funktionen 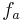 berücksichtigen, dass es sich um einen Fluss handelt, der zeitweise
austrocknet.
berücksichtigen, dass es sich um einen Fluss handelt, der zeitweise
austrocknet.
- Berechnung der Zeitpunkte, in denen der Fluss austrocknet
- Bestimmung der maximalen und minimalen Volumina
- Bestimmung der größten Senkung der Durchflussgeschwindigkeit
- Theoretische Fragen zur Wasserstandsaufgabe
- Berechnung des Wasservolumens in den ersten sechs Monaten
- Volumengleicheit zweier verschiedener Funktionen bis zum Zeitpunkt t0
Internetquellen

