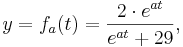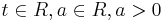Lösung a) aa): Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
 
(10 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
−
<math>y = f_{a}(t) = \frac{2\cdot e^{at}}{e^{at}+29}</math>, <math>t\in R, a\in R, a>0</math>
+
::<math>y = f_{a}(t) = \frac{2\cdot e^{at}}{e^{at}+29},</math> <math>t\in R, a\in R, a>0</math>
  
 
==Untersuchen sie das Verhalten der Funktionen f<sub>a</sub> für t -> <math>\pm  \infty </math> und geben sie für die Asymptoten Gleichungen an.==
 
==Untersuchen sie das Verhalten der Funktionen f<sub>a</sub> für t -> <math>\pm  \infty </math> und geben sie für die Asymptoten Gleichungen an.==
  
−
===<u>Verhalten gegen <math>+\infty </math></u>:===
+
'''<u>Verhalten gegen <math>+\infty </math></u>:'''
 
<math>\lim_{t \to \infty } f(t) = \lim_{t \to \infty } \frac{2\cdot e^{at} }{e^{at}+29 } = 2 \cdot \lim_{t \to \infty }\frac{e^{at} }{e^{at}+29 } = 2\cdot 1 = 2</math>
 
<math>\lim_{t \to \infty } f(t) = \lim_{t \to \infty } \frac{2\cdot e^{at} }{e^{at}+29 } = 2 \cdot \lim_{t \to \infty }\frac{e^{at} }{e^{at}+29 } = 2\cdot 1 = 2</math>
  
 
Da stets gilt a > 0, geht der Term <math>\lim_{t \to \infty } e^{at} </math> immer gegen <math>+\infty </math>;
 
Da stets gilt a > 0, geht der Term <math>\lim_{t \to \infty } e^{at} </math> immer gegen <math>+\infty </math>;
−
Daraus folgt nun, dass der Term <math>\lim_{t \to \infty } \frac{2\cdot e^{at} }{e^{at}+29 }</math> gegen 1 gehen muss, da 29 im Vergleich zu <math>+\infty </math> verschwinden klein ist.
+
Daraus folgt nun, dass der Term <math>\lim_{t \to \infty } \frac{2\cdot e^{at} }{e^{at}+29 }</math> gegen 1 gehen muss, da 29 im Vergleich zu <math>+\infty </math> vernachlässigbar klein ist.
  
−
===<u>Verhalten gegen <math>-\infty </math></u>:===
+
'''<u>Verhalten gegen <math>-\infty </math></u>:'''
 
<math>\lim_{t \to - \infty } f(t) = 2\cdot \lim_{t \to -\infty } \frac{e^{at}}{e^{at}+29 } = 2\cdot \frac{0}{29} = 0</math>
 
<math>\lim_{t \to - \infty } f(t) = 2\cdot \lim_{t \to -\infty } \frac{e^{at}}{e^{at}+29 } = 2\cdot \frac{0}{29} = 0</math>
  
 
Da stets gilt a > 0, geht der Term <math>\lim_{t \to - \infty } e^{at} </math> immer gegen 0; Daraus folgt, dass der Zähler gegen 0 geht und der Nenner gegen 29. Wenn man nun 0 durch 29 teilt, erkennt man, dass der Grenzwert <math>\lim_{t \to -\infty } f(t) </math> gegen 0 geht.
 
Da stets gilt a > 0, geht der Term <math>\lim_{t \to - \infty } e^{at} </math> immer gegen 0; Daraus folgt, dass der Zähler gegen 0 geht und der Nenner gegen 29. Wenn man nun 0 durch 29 teilt, erkennt man, dass der Grenzwert <math>\lim_{t \to -\infty } f(t) </math> gegen 0 geht.
  
−
===<u>Gleichungen der Asymptoten</u>:===
+
'''<u>Gleichungen der Asymptoten</u>:'''
  
 
* waagrechte Asymptote bei 0, wenn t -> <math>-\infty </math> geht
 
* waagrechte Asymptote bei 0, wenn t -> <math>-\infty </math> geht
Zeile 21: Zeile 21:
 
* waagrechte Asymptote bei 2, wenn t -> <math>+\infty </math> geht
 
* waagrechte Asymptote bei 2, wenn t -> <math>+\infty </math> geht
 
<math>\Rightarrow b(x) = 2</math>
 
<math>\Rightarrow b(x) = 2</math>
 +
 +
==Zeigen Sie, dass alle Funktionen f<sub>a</sub> monoton steigend sind==
 +
 +
<math>f'_{a} (t) = \frac{2\cdot a\cdot e^{at}\cdot (e^{at} + 29) - 2\cdot e^{at}\cdot a\cdot e^{at} }{(e^{at}+29) ^{2} } = 2\cdot a\cdot \frac{(e^{at}) ^{2} + 29\cdot e^{at} - (e^{at}) ^{2} }{(e^{at}+29) ^{2}} = \frac{58\cdot a\cdot e^{at} }{(e^{at}+29) ^{2}} </math>
 +
 +
 +
 +
Suche nach möglichem Extrempunkt; falls kein Extrempunkt vorhanden ist, zeigt dies, dass die Funktion monoton steigend oder fallend sein muss.
 +
 +
<math>f'_{a}(t)  = 0  \Rightarrow 58\cdot a\cdot e^{at} = 0 \Rightarrow e^{at} = 0\;\;\;\;\;\;(f)</math>
 +
 +
Da die e-Fkt. nie 0 werden kann, sondern dieser sich immer nur annähert, gibt es keine mögliche Stelle für einen Extrempunkt. Somit lässt sich folgern, dass die Funktion entweder streng monoton steigend oder fallend ist.
 +
 +
<br />
 +
'''Beweis dafür, dass die Funktion streng monoton steigend ist:'''
 +
 +
<br />
 +
Da man nun weiß, dass es keinen Extrempunkt gibt, an der sich das Monotonieverhalten ändern kann, lässt sich sehr leicht aus den Grenzwerten gegen <math>\pm  \infty </math> erkennnen, dass der Verlauf des Graphen stets steigend ist.
 +
 +
Der Grenzwert t -><math> - \infty </math> geht gegen 0<br />
 +
Der Grenzwert t -><math> \infty </math> geht gegen 2
 +
 +
Anhand dieser Grenzwerte und dem fehlenden Extrempunkt geht deutlich hervor, dass die Funktion einen streng monoton steigenden Verlauf nimmt, der sich 0 und 2 annähert
 +
  
  
 
[[Facharbeit Mathematik Straßheimer/Die Aufgabe|Zurück zur Aufgabe]]
 
[[Facharbeit Mathematik Straßheimer/Die Aufgabe|Zurück zur Aufgabe]]

Aktuelle Version vom 27. Januar 2010, 15:18 Uhr

y = f_{a}(t) = \frac{2\cdot e^{at}}{e^{at}+29}, t\in R, a\in R, a>0

Untersuchen sie das Verhalten der Funktionen fa für t -> 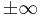\pm \infty und geben sie für die Asymptoten Gleichungen an.

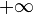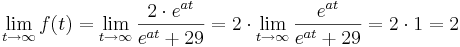
Verhalten gegen +\infty : \lim_{t \to \infty } f(t) = \lim_{t \to \infty } \frac{2\cdot e^{at} }{e^{at}+29 } = 2 \cdot \lim_{t \to \infty }\frac{e^{at} }{e^{at}+29 } = 2\cdot 1 = 2

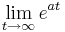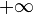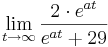Da stets gilt a > 0, geht der Term \lim_{t \to \infty } e^{at} immer gegen +\infty ; Daraus folgt nun, dass der Term \lim_{t \to \infty } \frac{2\cdot e^{at} }{e^{at}+29 } gegen 1 gehen muss, da 29 im Vergleich zu 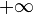+\infty vernachlässigbar klein ist.

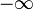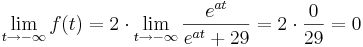
Verhalten gegen -\infty : \lim_{t \to - \infty } f(t) = 2\cdot \lim_{t \to -\infty } \frac{e^{at}}{e^{at}+29 } = 2\cdot \frac{0}{29} = 0

Da stets gilt a > 0, geht der Term 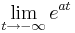\lim_{t \to - \infty } e^{at} immer gegen 0; Daraus folgt, dass der Zähler gegen 0 geht und der Nenner gegen 29. Wenn man nun 0 durch 29 teilt, erkennt man, dass der Grenzwert 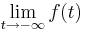\lim_{t \to -\infty } f(t) gegen 0 geht.

Gleichungen der Asymptoten:

  • waagrechte Asymptote bei 0, wenn t -> 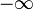-\infty geht

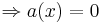
\Rightarrow a(x) = 0

  • waagrechte Asymptote bei 2, wenn t -> 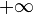+\infty geht

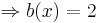
\Rightarrow b(x) = 2

Zeigen Sie, dass alle Funktionen fa monoton steigend sind

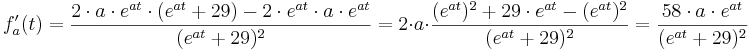
f'_{a} (t) = \frac{2\cdot a\cdot e^{at}\cdot (e^{at} + 29) - 2\cdot e^{at}\cdot a\cdot e^{at} }{(e^{at}+29) ^{2} } = 2\cdot a\cdot \frac{(e^{at}) ^{2} + 29\cdot e^{at} - (e^{at}) ^{2} }{(e^{at}+29) ^{2}} = \frac{58\cdot a\cdot e^{at} }{(e^{at}+29) ^{2}}


Suche nach möglichem Extrempunkt; falls kein Extrempunkt vorhanden ist, zeigt dies, dass die Funktion monoton steigend oder fallend sein muss.

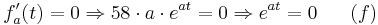
f'_{a}(t) = 0 \Rightarrow 58\cdot a\cdot e^{at} = 0 \Rightarrow e^{at} = 0\;\;\;\;\;\;(f)

Da die e-Fkt. nie 0 werden kann, sondern dieser sich immer nur annähert, gibt es keine mögliche Stelle für einen Extrempunkt. Somit lässt sich folgern, dass die Funktion entweder streng monoton steigend oder fallend ist.


Beweis dafür, dass die Funktion streng monoton steigend ist:


Da man nun weiß, dass es keinen Extrempunkt gibt, an der sich das Monotonieverhalten ändern kann, lässt sich sehr leicht aus den Grenzwerten gegen 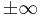\pm \infty erkennnen, dass der Verlauf des Graphen stets steigend ist.

Der Grenzwert t ->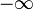 - \infty geht gegen 0
Der Grenzwert t -> \infty geht gegen 2

Anhand dieser Grenzwerte und dem fehlenden Extrempunkt geht deutlich hervor, dass die Funktion einen streng monoton steigenden Verlauf nimmt, der sich 0 und 2 annähert


Zurück zur Aufgabe

Von „http://rmg.zum.de/index.php?title=Facharbeit_Mathematik_Straßheimer/Die_Aufgabe/Lösung_a)_aa)&oldid=28387“