Die lineare Funktion: Unterschied zwischen den Versionen
(→Ufos versenken) |
K |
||
| (38 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0px; margin-right:90px; border: solid thin darkorange; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; "> | ||
| + | <span style="color: darkorange">'''Kurz zur Wiederholung:'''</span> | ||
| + | '''Proportionale Zuordnungen''' solltet ihr im Unterricht bereits besprochen haben. Eine solche Zuordnung liegt dann vor, wenn sich zwei Größen zueinander proportional verhalten. Das heißt sie steigen bzw. fallen im gleichen Verhältnis und haben somit immer einen konstanten Quotienten <math>q = \textstyle\frac{2.\;Gr \ddot osse}{1.\;Gr \ddot osse} </math>. (verdoppelt sich z.B. der Wert der x-Koordinate, so verdopplet sich auch der Wert der y-Koordinate)<br />Dies nennt man dann auch einen '''linearen Zusammenhang''', den man mit einer linearen Funktion beschreiben kann. Ihr Graph ist eine '''Gerade'''.</div><br /><br /><br /> | ||
| + | |||
== <span style="color: darkblue">Geradengleichung</span>== | == <span style="color: darkblue">Geradengleichung</span>== | ||
| Zeile 12: | Zeile 16: | ||
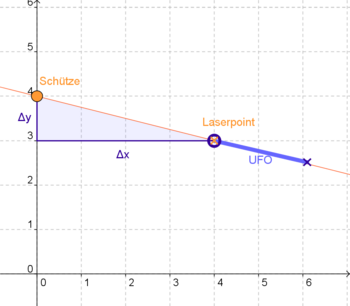
Peile mit dem Laserpoint (rotes Kreuz) jeweils den Bug (blauer Kreis) des Ufos an und richte dann die Schusslinie so aus, dass sie auch das Heck (blaues Kreuz) genau durchläuft. Hierzu kannst du sowohl Schütze als auch Laserpoint mit der Maus verschieben.<br /> | Peile mit dem Laserpoint (rotes Kreuz) jeweils den Bug (blauer Kreis) des Ufos an und richte dann die Schusslinie so aus, dass sie auch das Heck (blaues Kreuz) genau durchläuft. Hierzu kannst du sowohl Schütze als auch Laserpoint mit der Maus verschieben.<br /> | ||
Trage die Koordinaten anschließend auf deinem Arbeitsblatt ein und vergleiche zum Schluss deine Ergebnisse!<br /><br /> | Trage die Koordinaten anschließend auf deinem Arbeitsblatt ein und vergleiche zum Schluss deine Ergebnisse!<br /><br /> | ||
| − | |||
| + | '''Hier ein Beispiel...''' | ||
| + | {|width="99%" | ||
| + | |width="40%" style="vertical-align:top"| | ||
[[Bild:Beispiel.png|350px]] | [[Bild:Beispiel.png|350px]] | ||
| − | + | |width="5%" style="vertical-align:top"| | |
| + | |width="55%" style="vertical-align:center"| | ||
{| class="prettytable" align="center" | {| class="prettytable" align="center" | ||
| <span style="color: darkblue">Schütze</span> | | <span style="color: darkblue">Schütze</span> | ||
| Zeile 26: | Zeile 33: | ||
|} | |} | ||
Die Lage des Laserpoints gibst du mit den Koordinaten vom '''Schützen ausgehend''' an!<br /> | Die Lage des Laserpoints gibst du mit den Koordinaten vom '''Schützen ausgehend''' an!<br /> | ||
| + | |}<br /><br /> | ||
| + | |||
| + | <span style="color: orange">'''Der Schütze sagt nun:'''</span> '''"Alles klar! Ich schlage also den Kurs y = mx + t mit m = <math>\textstyle-\frac{1}{4}</math> und t = 4 ein!'''<br /> | ||
| + | Aber was bedeutet das? Vielleicht findest du es im Laufe des Spiels schon heraus...<br /><br /><br /> | ||
| + | |||
| + | '''Los geht´s...''' | ||
::::::::::::<ggb_applet height="500" width="700" filename="Ufos versenken.ggb" /><br /><br /><br /> | ::::::::::::<ggb_applet height="500" width="700" filename="Ufos versenken.ggb" /><br /><br /><br /> | ||
| Zeile 45: | Zeile 58: | ||
Du hast dem Schützen nun zwei wichtige Informationen mitgeteilt, mit deren Hilfe sich die Schusslinie - eine Gerade - aufstellen lässt. <br /> | Du hast dem Schützen nun zwei wichtige Informationen mitgeteilt, mit deren Hilfe sich die Schusslinie - eine Gerade - aufstellen lässt. <br /> | ||
Zuerst einmal die '''Steigung''' - Sie wird in der Mathematik mit '''m''' bezeichnet!<br /> | Zuerst einmal die '''Steigung''' - Sie wird in der Mathematik mit '''m''' bezeichnet!<br /> | ||
| − | Indem du vom Schützen ausgehend die Lage des Laserpoints ermittelt hast, hast du | + | Indem du vom Schützen ausgehend die Lage des Laserpoints ermittelt hast, hast du nichts anderes getan, als ein sogenanntes Steigunsdreieck zu beschreiben.<br /><br /> |
| − | : | + | |
| − | Im Beispiel gehen wir vom Punkt A | + | |
| − | um eine Einheit nach oben und kommen so bei Punkt B | + | {|width="99%" |
| + | |width="40%" style="vertical-align:top"| | ||
| + | [[Bild:Steigungsdreieck.png|450 px]] | ||
| + | |width="5%" style="vertical-align:top"| | ||
| + | |width="55%" style="vertical-align:center"| | ||
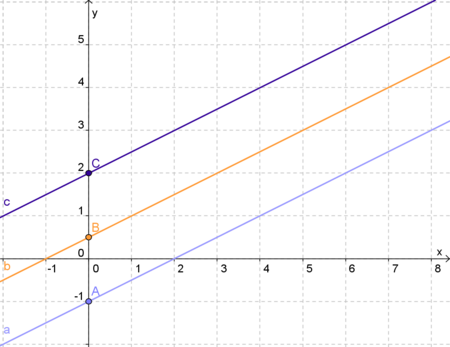
| + | Im nebenstehenden Beispiel gehen wir vom Punkt A (1|1) aus um 2 Einheiten nach rechts,<br /> | ||
| + | um eine Einheit nach oben und kommen so bei Punkt B (3|2) wieder an.<br /> Daraus entsteht das rechtwinklige <span style="color: darkorange">Steigungsdreieck</span>, dessen Katheten einmal<br /> | ||
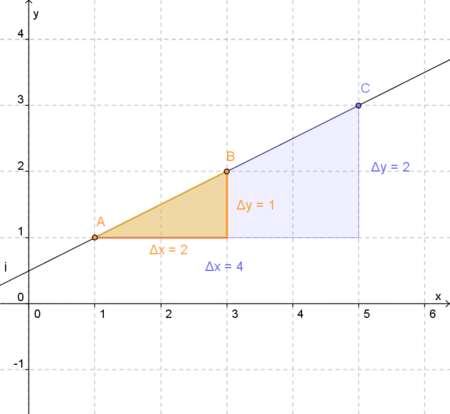
den waagrechten Zuwachs, <math>\triangle x</math>, und den Höhenzuwachs, <math>\triangle y</math>, anzeigen.<br /> <br /> | den waagrechten Zuwachs, <math>\triangle x</math>, und den Höhenzuwachs, <math>\triangle y</math>, anzeigen.<br /> <br /> | ||
<math>\triangle x</math> und <math>\triangle y</math> ist jeweils die Differenz aus den beiden x- bzw. y-Werten der Punkte A und B.<br /> | <math>\triangle x</math> und <math>\triangle y</math> ist jeweils die Differenz aus den beiden x- bzw. y-Werten der Punkte A und B.<br /> | ||
| − | → <math>\triangle x</math> = x<sub>B</sub> - x<sub>A</sub> = | + | → <math>\triangle x</math> = x<sub>B</sub> - x<sub>A</sub> = 3 - 1 = 2 <br /> |
→ <math>\triangle y</math> = y<sub>B</sub> - y<sub>A</sub> = 2 - 1 = 1<br /><br /> | → <math>\triangle y</math> = y<sub>B</sub> - y<sub>A</sub> = 2 - 1 = 1<br /><br /> | ||
Der Quotient "'''Höhenzuwachs''' durch '''waagrechten Zuwachs'''" ergibt die Steigung m.<br /> | Der Quotient "'''Höhenzuwachs''' durch '''waagrechten Zuwachs'''" ergibt die Steigung m.<br /> | ||
| − | m = <math>\frac{\triangle | + | m = <math> \textstyle\frac{\triangle y}{\triangle x}</math> = <math>\textstyle\frac{1}{2} </math> <br /> |
Dabei ist es völlig egal bei welchem Punkt man startet bzw. wie groß das Steigungsdreieck ist,<br /> | Dabei ist es völlig egal bei welchem Punkt man startet bzw. wie groß das Steigungsdreieck ist,<br /> | ||
da das Verhältnis der beiden Katheten immer das gleiche bleibt.<br /> | da das Verhältnis der beiden Katheten immer das gleiche bleibt.<br /> | ||
Nehmen wir zum Beipiel das zweite <span style="color: blue">Steigungsdreieck</span>:<br /> | Nehmen wir zum Beipiel das zweite <span style="color: blue">Steigungsdreieck</span>:<br /> | ||
| − | m = <math>\frac{2}{4}</math> = <math>\frac{1}{2}</math> <br /><br /> | + | m = <math>\textstyle\frac{2}{4}</math> = <math>\textstyle\frac{1}{2}</math> <br /><br /> |
Die Steigung m dieser Geraden beträgt also <u>an jeder Stelle</u> 0,5!<br /><br /> | Die Steigung m dieser Geraden beträgt also <u>an jeder Stelle</u> 0,5!<br /><br /> | ||
| + | |} | ||
<span style="color: darkorange">'''Arbeitsauftrag 1'''</span>: Verändere im GeoGebra-Applet am Schieberegler m ein paar mal die Steigung und versuche Aussagen über den Zusammenhang zwischen Steigung m und dem Aussehen des Graphen der Geraden zu machen!<br /> | <span style="color: darkorange">'''Arbeitsauftrag 1'''</span>: Verändere im GeoGebra-Applet am Schieberegler m ein paar mal die Steigung und versuche Aussagen über den Zusammenhang zwischen Steigung m und dem Aussehen des Graphen der Geraden zu machen!<br /> | ||
| − | ( Was kann man bei positivem bzw. negativem m beobachten? Wie verhält sich der Graph bei kleinerem bzw. größerem Betrag von m? Wie verhalten sich zwei Geraden mit der gleichen Steigung?)<br /><br /> | + | (Was kann man bei positivem bzw. negativem m beobachten? Wie verhält sich der Graph bei kleinerem bzw. größerem Betrag von m? Wie verhalten sich zwei Geraden mit der gleichen Steigung?)<br /><br /> |
| + | |||
<ggb_applet height="400" width="700" filename=" Steigungschieberegler.ggb" /><br /><br /> | <ggb_applet height="400" width="700" filename=" Steigungschieberegler.ggb" /><br /><br /> | ||
| Zeile 76: | Zeile 97: | ||
'''''Arbeitsauftrag 2:''''' | '''''Arbeitsauftrag 2:''''' | ||
| − | * Die Steigung im "Ufo-Beispiel" beträgt <math>-\frac{1}{4}</math>; <math> | + | * Die Steigung im "Ufo-Beispiel" beträgt <math>\textstyle-\frac{1}{4}</math>; m <math>=</math> <math>\textstyle-\frac{1}{4}</math> |
[[Bild:Arbeitsauftrag2.png|350px]] | [[Bild:Arbeitsauftrag2.png|350px]] | ||
}} | }} | ||
| Zeile 82: | Zeile 103: | ||
::::::::::::{| class="prettytable" | ::::::::::::{| class="prettytable" | ||
|- | |- | ||
| − | | 1 |'''Steigung m: m = <math>\frac{\triangle | + | | 1 |'''Steigung m: m = <math>\frac{\triangle y}{\triangle x}</math> = <math>\frac{H\ddot ohenzuwachs}{waagrechter\;Zuwachs}</math> '''<br /> |
|- | |- | ||
| Zeile 93: | Zeile 114: | ||
Jede Gerade schneidet in einem bestimmten Punkt die y-Achse! Das kann sowohl im positiven als auch im negativen Bereich passieren. | Jede Gerade schneidet in einem bestimmten Punkt die y-Achse! Das kann sowohl im positiven als auch im negativen Bereich passieren. | ||
Diesen Schnittpunkt mit der y-Achse nennt man '''y-Abschnitt''' - er wird gewöhnlich mit '''t''' bezeichnet.<br /><br /> | Diesen Schnittpunkt mit der y-Achse nennt man '''y-Abschnitt''' - er wird gewöhnlich mit '''t''' bezeichnet.<br /><br /> | ||
| − | + | ||
| − | + | ||
| − | + | {|width="99%" | |
| − | + | |width="40%" style="vertical-align:center"| | |
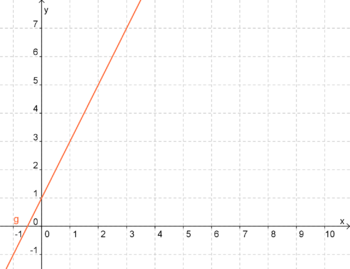
| − | + | Im Beipiel siehst du drei verschiedene Geraden, mit dem y-Abschnitt <br /> | |
| − | + | <span style="color: blue">t<sub>A</sub> = -1</span><br /> | |
| − | + | <span style="color: orange">t<sub>B</sub> = 0.5</span><br /> | |
| + | <span style="color: darkblue">t<sub>C</sub> = 2</span><br /><br /> | ||
| + | '''Ein positives t verschiebt also die Gerade ein Stück nach oben''' (vom Ursprung ausgehend),<br /> - es lässt sie im positiven Bereich mit der y-Achse schneiden.<br /><br /> | ||
| + | '''Ist t negativ, wird die Gerade nach unten verschoben.''' | ||
| + | |width="5%" style="vertical-align:top"| | ||
| + | |width="55%" style="vertical-align:top"| | ||
| + | [[Bild:y-Abschnitt.png|450 px]] | ||
| + | |}<br /><br /> | ||
| + | |||
<span style="color: darkorange">'''Arbeitsauftrag 1'''</span>: Zeichne auf deinem Arbeitsbaltt eine Gerade mit der Steigung m = 2 und dem y-Abschnitt t = 1 in das Koordinatensystem!<br /><br /> | <span style="color: darkorange">'''Arbeitsauftrag 1'''</span>: Zeichne auf deinem Arbeitsbaltt eine Gerade mit der Steigung m = 2 und dem y-Abschnitt t = 1 in das Koordinatensystem!<br /><br /> | ||
| Zeile 109: | Zeile 138: | ||
'''''Arbeitsauftrag 2:''''' | '''''Arbeitsauftrag 2:''''' | ||
| − | * Der y-Abschnitt t im "Ufo-Beispiel" liegt bei 4; t <math>=</math> 4 | + | * Der y-Abschnitt t im "Ufo-Beispiel" liegt bei 4; '''t <math>=</math> 4''' |
}} | }} | ||
| Zeile 126: | Zeile 155: | ||
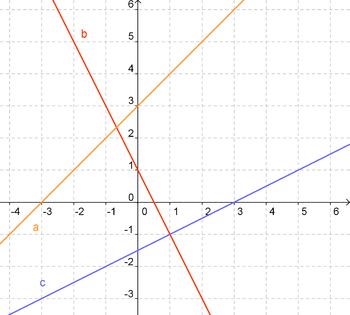
* '''<u>Ursprungsgerade</u>'''<br /> | * '''<u>Ursprungsgerade</u>'''<br /> | ||
| − | Als '''Ursprungsgeraden''' werden alle diejenigen Geraden bezeichnet, die den '''Ursprung P | + | Als '''Ursprungsgeraden''' werden alle diejenigen Geraden bezeichnet, die den '''Ursprung P (0|0)''' durchlaufen. <br /> |
'''<span style="color: darkorange">Arbeitsauftrag 1</span>''': Gib an welchen y-Abschnitt eine Ursprungsgerade hat!<br /><br /> | '''<span style="color: darkorange">Arbeitsauftrag 1</span>''': Gib an welchen y-Abschnitt eine Ursprungsgerade hat!<br /><br /> | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
'''''Arbeitsauftrag 1:''''' | '''''Arbeitsauftrag 1:''''' | ||
| − | * Der y-Abschnitt einer Ursprungsgerade lautet immer t <math>=</math> 0, da die Gerade die y-Achse im Punkt P<math> | + | * Der y-Abschnitt einer Ursprungsgerade lautet immer '''t <math>=</math> 0''', da die Gerade die y-Achse im Punkt P (0<math>|</math>0) schneidet. Ihre Geradengleichung sieht also folgendermaßen aus: y<math>=</math> mx; m kann beliebig gewählt werden, t muss 0 sein! |
}}<br /> | }}<br /> | ||
| Zeile 141: | Zeile 170: | ||
:::{{Lösung versteckt| | :::{{Lösung versteckt| | ||
'''''Arbeitsauftrag 2:''''' | '''''Arbeitsauftrag 2:''''' | ||
| − | * Das lässt sich leicht erkennen, da die beiden Koordinatenachsen immer senkrecht aufeinander stehen, d.h. zwischen ihnen liegt ein Winkel von 90°. Die Winkelhalbierende, die dieses Winkelfeld genau teilt, schließt also mit beiden Koordinatenachsen jeweils einen Winkel von 45° ein! | + | * Das lässt sich leicht erkennen, da die beiden Koordinatenachsen immer senkrecht aufeinander stehen, d.h. zwischen ihnen liegt ein Winkel von 90°. Die Winkelhalbierende, die dieses Winkelfeld genau teilt, schließt also mit beiden Koordinatenachsen jeweils einen Winkel von '''45°''' ein! |
}}<br /> | }}<br /> | ||
| Zeile 149: | Zeile 178: | ||
::::::{{Lösung versteckt| | ::::::{{Lösung versteckt| | ||
'''''Arbeitsauftrag 3:''''' | '''''Arbeitsauftrag 3:''''' | ||
| − | * Die Geradengleichung für Parallele zur x-Achse lautet y<math>=</math> t. Da eine zur x-Achse parallele Gerade weder steigt noch fällt, sondern einfach waagrecht verläuft, gilt: m <math>=</math> 0.<br /> Somit fällt in der Gleichung auch das mit 0 multiplizierte x weg | + | * Die Geradengleichung für Parallele zur x-Achse lautet '''y<math>=</math> t'''. Da eine zur x-Achse parallele Gerade weder steigt noch fällt, sondern einfach waagrecht verläuft, gilt: m <math>=</math> 0.<br /> Somit fällt in der Gleichung auch das mit 0 multiplizierte x weg; t ist beliebig! |
}}<br /> | }}<br /> | ||
== <span style="color: darkblue">Zusammenfassung</span>== | == <span style="color: darkblue">Zusammenfassung</span>== | ||
| − | Eine Funktion der Form | + | Eine Funktion der Form f(x) = mx + t heißt '''lineare Funktion'''. Der Graph einer linearen Funktion ist eine '''Gerade'''.<br /><br /> |
Eine Gerade hat die '''Steigung m''' und den '''y-Abschnitt t'''. <br /><br /> | Eine Gerade hat die '''Steigung m''' und den '''y-Abschnitt t'''. <br /><br /> | ||
| − | '''m ='''<math>\frac{\triangle | + | '''m ='''<math>\textstyle\frac{\triangle y}{\triangle x}</math><br /> |
'''m > 0''' → Gerade steigt<br /> | '''m > 0''' → Gerade steigt<br /> | ||
'''m < 0''' → Gerade fällt<br /> | '''m < 0''' → Gerade fällt<br /> | ||
| Zeile 169: | Zeile 198: | ||
Zusammen bilden sie die '''Geradengleichung''' <br /> | Zusammen bilden sie die '''Geradengleichung''' <br /> | ||
| − | ''' | + | '''y = m x + t'''<br /><br /> |
| + | |||
| + | <u>Oft wird von f(x) = mx + t die Rede sein. Diese Form ist gleichbedeutend mit y = mx + t,<br /> | ||
| + | da die Geradengleichung einfach eine besondere Form der '''Funktionsgleichung''' ist!</u> | ||
== <span style="color: darkblue">Aufgaben</span>== | == <span style="color: darkblue">Aufgaben</span>== | ||
1. Lies aus den folgenden Geradengleichungen sowohl die Steigung als auch den y-Abschnitt ab! | 1. Lies aus den folgenden Geradengleichungen sowohl die Steigung als auch den y-Abschnitt ab! | ||
| − | + | a) y = 2x - 4 <br /> | |
| − | + | b) y = <math>\textstyle\frac{1}{3}</math> x + 2<br /> | |
| − | + | c) y = -<math>\textstyle\frac{2}{5}</math> x + 1 <br /> | |
| − | + | d) y = 3x - 0,5 | |
<br /> | <br /> | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
| − | a) m <math>=</math> 2; t <math>=</math> -4<br /> | + | a) '''m <math>=</math> 2'''; '''t <math>=</math> -4'''<br /> |
| − | b) m <math>=</math> <math>\frac{1}{3}</math>; t <math>=</math> 2<br /> | + | b) '''m <math>=</math> <math>\textstyle\frac{1}{3}</math>'''; '''t <math>=</math> 2'''<br /> |
| − | c) m <math>=</math> -<math>\frac{2}{5}</math>; t <math>=</math> 1<br /> | + | c) '''m <math>=</math> -<math>\textstyle\frac{2}{5}</math>'''; '''t <math>=</math> 1'''<br /> |
| − | d) m <math>=</math> 3; t <math>=</math> -0,5 | + | d) '''m <math>=</math> 3'''; '''t <math>=</math> -0,5''' |
}}<br /> | }}<br /> | ||
| − | 2. | + | 2. Zeichne die Graphen der folgenden Geraden!<br /> |
| − | + | a) y = -x<br /> | |
| − | + | b) y = -2<br /> | |
| − | + | c) y = <math>\textstyle\frac{1}{2}</math> x - 1<br /> | |
| − | + | d) y = -1,5x + 2 | |
<br /> | <br /> | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
| Zeile 196: | Zeile 228: | ||
}}<br /> | }}<br /> | ||
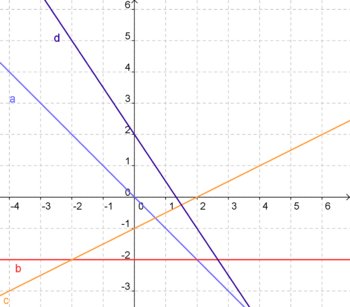
| − | 3. Ordne den dargestellten Geraden jeweils eine Geradengleichung zu! | + | 3. Ordne den dargestellten Geraden jeweils eine Geradengleichung zu!<br /> |
<br /> | <br /> | ||
:::::::::::::[[Bild:Geraden.jpg|350px]] | :::::::::::::[[Bild:Geraden.jpg|350px]] | ||
<br /> | <br /> | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
| − | a) y <math>=</math> x + 3<br /> | + | a) '''y <math>=</math> x + 3'''<br /> |
| − | b) y <math>=</math> -2x + 1<br /> | + | b) '''y <math>=</math> -2x + 1'''<br /> |
| − | c) y <math>=</math> <math>\frac{1}{2}</math>x - 1,5 | + | c) '''y <math>=</math> <math>\textstyle\frac{1}{2}</math>x - 1,5''' |
}}<br /> | }}<br /> | ||
4. Sind die folgenden Funktionen linear? Begründe jeweils deine Entscheidung! | 4. Sind die folgenden Funktionen linear? Begründe jeweils deine Entscheidung! | ||
| − | + | a) f(x) = 23 - 15x<br /> | |
| − | + | b) f(x) = 2x² - 4<br /> | |
| − | + | c) f(x) = 3x + 0,5x | |
<br /> | <br /> | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
a) f(x) <math>=</math> -15x + 23; so umgestellt erkennt man leicht die Geradengleichung. Die Funktion ist also '''linear'''!<br /> | a) f(x) <math>=</math> -15x + 23; so umgestellt erkennt man leicht die Geradengleichung. Die Funktion ist also '''linear'''!<br /> | ||
| − | b) Die Funktion ist '''nicht linear''', da der x-Wert und er Funktionswert sich nicht im gleichen Verhältnis verändern! (Beispiel: f(2) <math>=</math> 4; f(4) <math>=</math> 28 → der x-Wert wird verdoppelt, während der Funktionswert, also y, nun 7mal so groß ist)<br />c) f(x) <math>=</math> 3,5x; so | + | b) Die Funktion ist '''nicht linear''', da der x-Wert und er Funktionswert sich nicht im gleichen Verhältnis verändern! (Beispiel: f(2) <math>=</math> 4; f(4) <math>=</math> 28 → der x-Wert wird verdoppelt, während der Funktionswert, also y, nun 7mal so groß ist)<br />c) f(x) <math>=</math> 3,5x; so vereinfacht ist auch diese Funktionsgleichung eine Geradengleichung. Die Funktion ist '''linear'''! |
}}<br /> | }}<br /> | ||
5. Gib zu den in Worten genannten Vorschriften jeweils eine Funktionsgleichung an! | 5. Gib zu den in Worten genannten Vorschriften jeweils eine Funktionsgleichung an! | ||
| − | + | a) Jedem x wird das Doppelte zugeordnet.<br /> | |
| − | + | b) Jedem x wird das um 3 verminderte Vierfache zugeordnet.<br /> | |
| − | + | c) Jedem x wird das um 2 vergrößerte Dreifache zugeordnet. | |
<br /> | <br /> | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
| − | a) f(x) <math>=</math> 2x<br /> | + | a) '''f(x) <math>=</math> 2x'''<br /> |
| − | b) f(x) <math>=</math> 4x - 3<br /> | + | b) '''f(x) <math>=</math> 4x - 3'''<br /> |
| − | c) f(x) <math>=</math> 3x + 2 | + | c) '''f(x) <math>=</math> 3x + 2''' |
}}<br /> | }}<br /> | ||
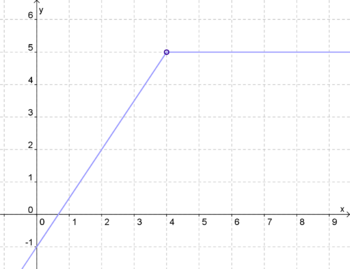
| − | 6. Zeichne die | + | 6. Zeichne die Graphen der abschnittsweise defienierten Funktion! [[Digitaler Lernpfad zu linearen Funktionen/Inhaltsverzeichnis/Grundwissensübersicht|Grundwissensübersicht]] |
| − | + | a) f(x) = <math>\begin{cases} 1,5x-1, & \mbox{wenn }x\mbox{ kleiner 4} \\ 5, & \mbox{wenn }x\mbox{ groesser 4} \end{cases} </math> | |
<br /> | <br /> | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
| Zeile 237: | Zeile 269: | ||
}}<br /> | }}<br /> | ||
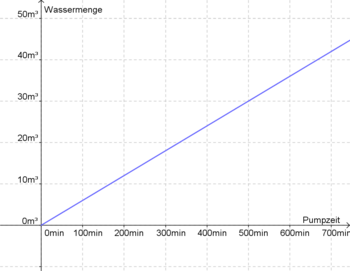
| − | 7. Das Badewaser eines kleinen Gartenswimmingpools wird mit einer Gartenpumpe gleichmäßig | + | 7. Das Badewaser eines kleinen Gartenswimmingpools wird mit einer Gartenpumpe gleichmäßig eingelassen. Der vollständig befüllte Gartenpool fasst eine Wassermenge von 40 m³.<br /> |
| − | + | <br /> | |
| − | ::a) Wie groß ist die Wassermenge, die innerhalb einer Stunde | + | ::::::::::::[[Bild:aufgabe7.png|350px]] |
| − | + | <br /> | |
| − | : | + | a) Beschreibe mit eigenen Worten das dargestellte Diagramm!<br /> |
| + | b) Wie groß ist die Wassermenge, die innerhalb einer Stunde zugeführt wird?<br /> | ||
| + | c) Gib eine Funktionsgleichung zum Graphen an! | ||
| + | <br /> | ||
| + | {{Lösung versteckt| | ||
| + | a) Das Diagramm stellt die zugeführte Wassermenge in m³ in Abhängigkeit der Pumpzeit in min dar. Es handelt sich um einen linearen Zusammenhang, da der Graph der Funktion eine Gerade ist.<br /> | ||
| + | b) In einer Stunde werden '''3,6 m³''' Wasser zugeführt. Am einfachsten betrachtet man hierzu die Wassermenge bei 500 min: <math>\textstyle\frac{30}{500}</math> · 60 <math>=</math> 3,6<br /> | ||
| + | c) '''f(x) <math>=</math> 0,06x'''. Stellt man sich ein Steigungsdreieck vor, so kommt man schnell auf den Wert von m. t ist natürlich null, da es sich um ein Ursprungsgerade handelt.<br /> | ||
| + | }}<br /> | ||
Aktuelle Version vom 27. Januar 2010, 16:56 Uhr
Kurz zur Wiederholung:
Proportionale Zuordnungen solltet ihr im Unterricht bereits besprochen haben. Eine solche Zuordnung liegt dann vor, wenn sich zwei Größen zueinander proportional verhalten. Das heißt sie steigen bzw. fallen im gleichen Verhältnis und haben somit immer einen konstanten Quotienten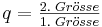 . (verdoppelt sich z.B. der Wert der x-Koordinate, so verdopplet sich auch der Wert der y-Koordinate)
. (verdoppelt sich z.B. der Wert der x-Koordinate, so verdopplet sich auch der Wert der y-Koordinate)Dies nennt man dann auch einen linearen Zusammenhang, den man mit einer linearen Funktion beschreiben kann. Ihr Graph ist eine Gerade.
Inhaltsverzeichnis |
Geradengleichung
Ufos versenken
Zuerst einmal die wichtigste Grundlage, um mit linearen Funktionen umgehen zu können - die Geradengleichung.
Sie legt eine solche Funktion eindeutig fest.
Zum Einstieg ein kleines Spiel!
Beim Ufos versenken geht es darum dem Schützen so genau wie möglich die Daten für die Schusslinie mitzuteilen, damit dieser dann erfolgreich die feindlichen Ufos abwehren kann.
Er muss zum einen wissen von welcher Position aus er schießen muss und zum andern welche Richtung er anpeilen muss.
Peile mit dem Laserpoint (rotes Kreuz) jeweils den Bug (blauer Kreis) des Ufos an und richte dann die Schusslinie so aus, dass sie auch das Heck (blaues Kreuz) genau durchläuft. Hierzu kannst du sowohl Schütze als auch Laserpoint mit der Maus verschieben.
Trage die Koordinaten anschließend auf deinem Arbeitsblatt ein und vergleiche zum Schluss deine Ergebnisse!
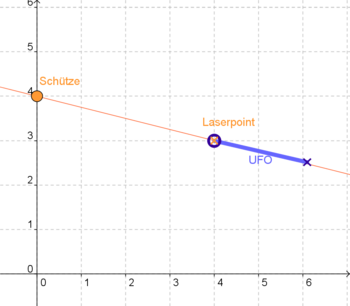
Hier ein Beispiel...
Die Lage des Laserpoints gibst du mit den Koordinaten vom Schützen ausgehend an! |
Der Schütze sagt nun: "Alles klar! Ich schlage also den Kurs y = mx + t mit m = 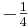 und t = 4 ein!
und t = 4 ein!
Aber was bedeutet das? Vielleicht findest du es im Laufe des Spiels schon heraus...
Los geht´s...
Das Steigungsdreieck
Du hast dem Schützen nun zwei wichtige Informationen mitgeteilt, mit deren Hilfe sich die Schusslinie - eine Gerade - aufstellen lässt.
Zuerst einmal die Steigung - Sie wird in der Mathematik mit m bezeichnet!
Indem du vom Schützen ausgehend die Lage des Laserpoints ermittelt hast, hast du nichts anderes getan, als ein sogenanntes Steigunsdreieck zu beschreiben.
|
Im nebenstehenden Beispiel gehen wir vom Punkt A (1|1) aus um 2 Einheiten nach rechts, |
Arbeitsauftrag 1: Verändere im GeoGebra-Applet am Schieberegler m ein paar mal die Steigung und versuche Aussagen über den Zusammenhang zwischen Steigung m und dem Aussehen des Graphen der Geraden zu machen!
(Was kann man bei positivem bzw. negativem m beobachten? Wie verhält sich der Graph bei kleinerem bzw. größerem Betrag von m? Wie verhalten sich zwei Geraden mit der gleichen Steigung?)
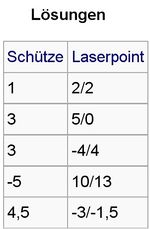
Arbeitsauftrag 2: Versuche die Steigung unseres "Ufo-Beispiels" zu bestimmen! Zeichne dazu ein geeignetes Steigungsdreieck in die Grafik auf deinem Arbeitsblatt ein und beschrifte es entsprechend!
Arbeitsauftrag 1:
- Ist die Steigung m positiv, so steigt die Gerade - d.h. ihr Graf verläuft von links unten nach rechts oben. Die Gerade fällt dagegen, wenn m negativ ist.
- Je kleiner der Betrag von m, desto flacher verläuft der Graf. Bei größer werdendem m wird er immer steiler.
- Zwei Geraden mit gleichem m, also der gleichen Steigung, sind parallel!
Arbeitsauftrag 2:
- Die Steigung im "Ufo-Beispiel" beträgt
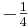 ; m
; m 
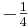
Steigung m: m = 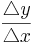 =
= 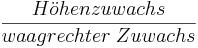
Der y-Abschnitt
Die zweite wichtige Information hast du gewissermaßen mit der Lage des Schützen angegeben.
Jede Gerade schneidet in einem bestimmten Punkt die y-Achse! Das kann sowohl im positiven als auch im negativen Bereich passieren.
Diesen Schnittpunkt mit der y-Achse nennt man y-Abschnitt - er wird gewöhnlich mit t bezeichnet.
|
Im Beipiel siehst du drei verschiedene Geraden, mit dem y-Abschnitt |
Arbeitsauftrag 1: Zeichne auf deinem Arbeitsbaltt eine Gerade mit der Steigung m = 2 und dem y-Abschnitt t = 1 in das Koordinatensystem!
Arbeitsauftrag 2: Bestimme wieder den y-Abschnitt des "Ufo-Beispiels"!
y-Abschnitt t: Schnittpunkt der Geraden mit der y-Achse
Besondere Geraden
- Ursprungsgerade
Als Ursprungsgeraden werden alle diejenigen Geraden bezeichnet, die den Ursprung P (0|0) durchlaufen.
Arbeitsauftrag 1: Gib an welchen y-Abschnitt eine Ursprungsgerade hat!
Arbeitsauftrag 1:
- Der y-Abschnitt einer Ursprungsgerade lautet immer t
 0, da die Gerade die y-Achse im Punkt P (0
0, da die Gerade die y-Achse im Punkt P (0 0) schneidet. Ihre Geradengleichung sieht also folgendermaßen aus: y
0) schneidet. Ihre Geradengleichung sieht also folgendermaßen aus: y mx; m kann beliebig gewählt werden, t muss 0 sein!
mx; m kann beliebig gewählt werden, t muss 0 sein!
- Winkelhalbierende
- Winkelhalbierende
- Die Winkelhalbierenden im Koordinatensystem sind diejenigen Geraden, die den 1. & 3. bzw. 2. & 4. Quadranten in jeweils zwei gleichgroße Teile teilen.
- Die Winkelhalbierenden im Koordinatensystem sind diejenigen Geraden, die den 1. & 3. bzw. 2. & 4. Quadranten in jeweils zwei gleichgroße Teile teilen.
- Arbeitsauftrag 2: Gib den Winkel an, unter dem die Winkelhalbierende die x- bzw. y-Achse dann schneidet!
- Arbeitsauftrag 2: Gib den Winkel an, unter dem die Winkelhalbierende die x- bzw. y-Achse dann schneidet!
Arbeitsauftrag 2:
- Das lässt sich leicht erkennen, da die beiden Koordinatenachsen immer senkrecht aufeinander stehen, d.h. zwischen ihnen liegt ein Winkel von 90°. Die Winkelhalbierende, die dieses Winkelfeld genau teilt, schließt also mit beiden Koordinatenachsen jeweils einen Winkel von 45° ein!
- Parallele zur x-Achse
- Parallele zur x-Achse
- Arbeitsauftrag 3: Überlege wie die Geradengleichung einer zur x-Achse parallelen Geraden lautet!
- Arbeitsauftrag 3: Überlege wie die Geradengleichung einer zur x-Achse parallelen Geraden lautet!
Arbeitsauftrag 3:
- Die Geradengleichung für Parallele zur x-Achse lautet y
 t. Da eine zur x-Achse parallele Gerade weder steigt noch fällt, sondern einfach waagrecht verläuft, gilt: m
t. Da eine zur x-Achse parallele Gerade weder steigt noch fällt, sondern einfach waagrecht verläuft, gilt: m  0.
0.
Somit fällt in der Gleichung auch das mit 0 multiplizierte x weg; t ist beliebig!
Zusammenfassung
Eine Funktion der Form f(x) = mx + t heißt lineare Funktion. Der Graph einer linearen Funktion ist eine Gerade.
Eine Gerade hat die Steigung m und den y-Abschnitt t.
m =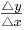
m > 0 → Gerade steigt
m < 0 → Gerade fällt
Je größer |m| umso steiler die Gerade!
Geraden mit gleichem m sind parallel!
t > 0 → die Gerade schneidet die y-Achse oberhalb des Ursprungs
t < 0 → die Gerade schneidet die y-Achse unterhalb des Ursprungs
m und t sind feste Zahlen, Parameter, die die Gerade eindeutig festlegen.
Im Gegensatz dazu sind x und y unbekannte Größen, Variablen.
Zusammen bilden sie die Geradengleichung
y = m x + t
Oft wird von f(x) = mx + t die Rede sein. Diese Form ist gleichbedeutend mit y = mx + t,
da die Geradengleichung einfach eine besondere Form der Funktionsgleichung ist!
Aufgaben
1. Lies aus den folgenden Geradengleichungen sowohl die Steigung als auch den y-Abschnitt ab!
a) y = 2x - 4
b) y = 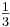 x + 2
x + 2
c) y = -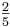 x + 1
x + 1
d) y = 3x - 0,5
a) m  2; t
2; t  -4
-4
b) m 
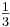 ; t
; t  2
2
c) m  -
-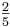 ; t
; t  1
1
d) m  3; t
3; t  -0,5
-0,5
2. Zeichne die Graphen der folgenden Geraden!
a) y = -x
b) y = -2
c) y = 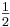 x - 1
x - 1
d) y = -1,5x + 2
3. Ordne den dargestellten Geraden jeweils eine Geradengleichung zu!
a) y  x + 3
x + 3
b) y  -2x + 1
-2x + 1
c) y 
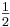 x - 1,5
x - 1,5
4. Sind die folgenden Funktionen linear? Begründe jeweils deine Entscheidung!
a) f(x) = 23 - 15x
b) f(x) = 2x² - 4
c) f(x) = 3x + 0,5x
a) f(x)  -15x + 23; so umgestellt erkennt man leicht die Geradengleichung. Die Funktion ist also linear!
-15x + 23; so umgestellt erkennt man leicht die Geradengleichung. Die Funktion ist also linear!
b) Die Funktion ist nicht linear, da der x-Wert und er Funktionswert sich nicht im gleichen Verhältnis verändern! (Beispiel: f(2)  4; f(4)
4; f(4)  28 → der x-Wert wird verdoppelt, während der Funktionswert, also y, nun 7mal so groß ist)
28 → der x-Wert wird verdoppelt, während der Funktionswert, also y, nun 7mal so groß ist)
c) f(x)  3,5x; so vereinfacht ist auch diese Funktionsgleichung eine Geradengleichung. Die Funktion ist linear!
3,5x; so vereinfacht ist auch diese Funktionsgleichung eine Geradengleichung. Die Funktion ist linear!
5. Gib zu den in Worten genannten Vorschriften jeweils eine Funktionsgleichung an!
a) Jedem x wird das Doppelte zugeordnet.
b) Jedem x wird das um 3 verminderte Vierfache zugeordnet.
c) Jedem x wird das um 2 vergrößerte Dreifache zugeordnet.
a) f(x)  2x
2x
b) f(x)  4x - 3
4x - 3
c) f(x)  3x + 2
3x + 2
6. Zeichne die Graphen der abschnittsweise defienierten Funktion! Grundwissensübersicht
a) f(x) = 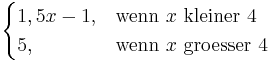
7. Das Badewaser eines kleinen Gartenswimmingpools wird mit einer Gartenpumpe gleichmäßig eingelassen. Der vollständig befüllte Gartenpool fasst eine Wassermenge von 40 m³.
a) Beschreibe mit eigenen Worten das dargestellte Diagramm!
b) Wie groß ist die Wassermenge, die innerhalb einer Stunde zugeführt wird?
c) Gib eine Funktionsgleichung zum Graphen an!
a) Das Diagramm stellt die zugeführte Wassermenge in m³ in Abhängigkeit der Pumpzeit in min dar. Es handelt sich um einen linearen Zusammenhang, da der Graph der Funktion eine Gerade ist.
b) In einer Stunde werden 3,6 m³ Wasser zugeführt. Am einfachsten betrachtet man hierzu die Wassermenge bei 500 min: 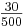 · 60
· 60  3,6
3,6
c) f(x)  0,06x. Stellt man sich ein Steigungsdreieck vor, so kommt man schnell auf den Wert von m. t ist natürlich null, da es sich um ein Ursprungsgerade handelt.
0,06x. Stellt man sich ein Steigungsdreieck vor, so kommt man schnell auf den Wert von m. t ist natürlich null, da es sich um ein Ursprungsgerade handelt.
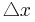 , und den Höhenzuwachs,
, und den Höhenzuwachs, 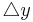 , anzeigen.
, anzeigen.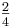 =
=