Mathematik 10: Unterschied zwischen den Versionen
Aus RMG-Wiki
(Bild eingefügt) |
|||
| Zeile 86: | Zeile 86: | ||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ==== 6. Lineares und exponentielles Wachstum==== | ||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | {{#ev:youtube |plmnJEM6G0k|400}} | ||
| + | |||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
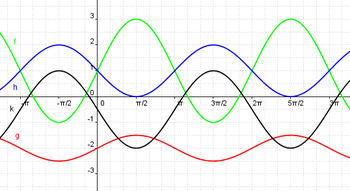
| + | *[[Media:Die trigonometrischen Funktionen im Überblick.doc|Überblick trigonometrische Funktionen]] | ||
| + | </td></tr></table></center> | ||
<center><table border="0" width="800px" cellpadding=5 cellspacing=15> | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
Version vom 16. November 2014, 14:15 Uhr
1. BMT am 2.10.2014Grundwissen des RMG: 5. Klasse - 6. Klasse - 7. Klasse - 8. Klasse - 9. Klasse Wiederholungsaufgaben mit Lösungen:
BMT: |
2. Kreis und Kugel1. Die Kreiszahl Pi 2. Kreissektor und Bogenmaß
|
3. Sinus- und Kosinus am Einheitskreis
|
4. Sinus- und Kosinusfunktion |
5. Die allgemeine Sinusfunktion |
6. Lineares und exponentielles Wachstum
|
10. Ganzrationale Funktionen
|
9. Bedingte Wahrscheinlichkeit |
8. Potenzfunktion
|
7. Exponentialfunktion
|
Mathematik und Kunst
|