Höhen: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: 1234)
 
 
(30 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
−
1234
+
<br><br>
 +
=<span style="background:RoyalBlue1">Die Höhen im Dreieck</span>=
 +
 
 +
<div style="margin:0px; margin-right:90px; border:thick double green; padding: 1em 1em 1em 1em; background-color:white;  width:60%; align:center; ">
 +
<span style="color: green">'''Arbeitsaufträge:'''</span>
 +
*Folge der Konstruktionsbeschreibung, um ein Dreieck und die Höhe h<sub>c</sub> mit GeoGebra zu konstruieren.
 +
*Konstruiere nun mit Hilfe von GeoGebra die Höhen h<sub>a</sub> und h<sub>b</sub>.
 +
*Vergleiche deine Konstruktion mit der Lösung.
 +
</div>
 +
 
 +
<ggb_applet height="50" width="150" type="button" filename="GeoGebra Vorlage.ggb" />
 +
 
 +
<div style="margin:0px; margin-right:90px; border:thick double blue; padding: 1em 1em 1em 1em; background-color:white;  width:75%; align:center; ">
 +
<span style="color: blue">'''Konstruktionsbeschreibung:'''</span>
 +
 
 +
1. Konstruiere ein Dreieck mit A(2|1), B(8|1) und C(6|6). ''Verwende dazu den Button Vieleck. [[Bild:Button Vieleck.jpg]]''
 +
 
 +
2. Zeichne eine senkrechte Gerade d von der Strecke c durch den Punkt C. ''Klicke dazu auf den Button Senkrechte Gerade [[Bild:Button Senkrechte Gerade.jpg]] und dann auf die Strecke c und den Punkt C.''
 +
 
 +
3. Schneide die Strecke c mit der Geraden d. ''Verwende dazu den Button Schneide zwei Objekte. [[Bild:Button Schneide zwei Objekte.jpg]]''
 +
 
 +
4. Verstecke die Gerade d. ''Rechte Maustaste: Objekt anzeigen''
 +
 
 +
5. Zeichne eine Strecke von C zu D ''mit dem Button Strecke zwischen zwei Punkten. [[Bild:Button Strecke zwischen zwei Punkten.jpg]]''
 +
 
 +
6. Verstecke den Punkt D. ''Rechte Maustaste: Objekt anzeigen''
 +
 
 +
<br>
 +
 
 +
7. Nenne die Strecke e in h_c um. ''Rechte Maustaste: Umbenennen''
 +
 
 +
<br>
 +
 
 +
8. Färbe h<sub>c</sub> rot ein. ''Rechte Maustaste: Eigenschaften: Farbe''
 +
 
 +
<br>
 +
 
 +
9. Konstruiere h<sub>a</sub> und h<sub>b</sub> wie in den Schritten 2-8.
 +
 
 +
 
 +
</div>
 +
 
 +
 
 +
<br>
 +
{{Lösung versteckt|
 +
<br>
 +
'''Jede Seite des Dreiecks hat eine zugehörige Höhe, somit hat ein Dreieck drei Höhen.'''
 +
<br><br>
 +
'''Beim Dreieck muss nicht immer c die Grundlinie sein.
 +
Wie berechnest du den Flächeninhalt, wenn...
 +
 
 +
...a und h<sub>a</sub> gegeben sind?
 +
 
 +
...b und h<sub>b</sub> gegeben sind?
 +
 
 +
Lösung:{{versteckt|
 +
:'''A<math>=</math>a<math>\cdot</math>h<sub>a</sub> : 2'''
 +
 
 +
:'''A<math>=</math>b<math>\cdot</math>h<sub>b</sub> : 2'''
 +
}}
 +
<br>
 +
'''Flächenformel für das Dreieck: A<sub>Dreieck</sub> <math>=</math> (Grundlinie<math>\cdot</math>Höhe<sub>Grundlinie</sub>) : 2'''
 +
<br><br>
 +
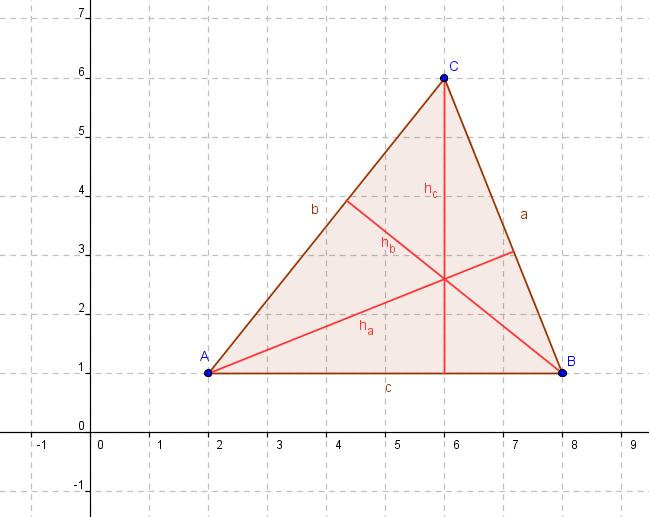
[[Bild:Dreieck Höhe Lösung.jpg]]
 +
 
 +
}}
 +
<br>
 +
 
 +
----
 +
<big>[[Lernpfad Flächenberechnung/Inhaltsverzeichnis/Dreieck/Höhen/Übungen|Hier]] </big> kommst du zu weiteren Übungsaufgaben.

Aktuelle Version vom 26. September 2010, 22:31 Uhr



Die Höhen im Dreieck

Arbeitsaufträge:

  • Folge der Konstruktionsbeschreibung, um ein Dreieck und die Höhe hc mit GeoGebra zu konstruieren.
  • Konstruiere nun mit Hilfe von GeoGebra die Höhen ha und hb.
  • Vergleiche deine Konstruktion mit der Lösung.

Konstruktionsbeschreibung:

1. Konstruiere ein Dreieck mit A(2|1), B(8|1) und C(6|6). Verwende dazu den Button Vieleck. Button Vieleck.jpg

2. Zeichne eine senkrechte Gerade d von der Strecke c durch den Punkt C. Klicke dazu auf den Button Senkrechte Gerade Button Senkrechte Gerade.jpg und dann auf die Strecke c und den Punkt C.

3. Schneide die Strecke c mit der Geraden d. Verwende dazu den Button Schneide zwei Objekte. Button Schneide zwei Objekte.jpg

4. Verstecke die Gerade d. Rechte Maustaste: Objekt anzeigen

5. Zeichne eine Strecke von C zu D mit dem Button Strecke zwischen zwei Punkten. Button Strecke zwischen zwei Punkten.jpg

6. Verstecke den Punkt D. Rechte Maustaste: Objekt anzeigen


7. Nenne die Strecke e in h_c um. Rechte Maustaste: Umbenennen


8. Färbe hc rot ein. Rechte Maustaste: Eigenschaften: Farbe


9. Konstruiere ha und hb wie in den Schritten 2-8.





Jede Seite des Dreiecks hat eine zugehörige Höhe, somit hat ein Dreieck drei Höhen.

Beim Dreieck muss nicht immer c die Grundlinie sein. Wie berechnest du den Flächeninhalt, wenn...

...a und ha gegeben sind?

...b und hb gegeben sind?

Lösung:

A=a\cdotha : 2
A=b\cdothb : 2


Flächenformel für das Dreieck: ADreieck = (Grundlinie\cdotHöheGrundlinie) : 2

Dreieck Höhe Lösung.jpg


Hier kommst du zu weiteren Übungsaufgaben.

Von „http://rmg.zum.de/index.php?title=Lernpfad_Flächenberechnung/Inhaltsverzeichnis/Dreieck/Höhen&oldid=35734“