Höhen: Unterschied zwischen den Versionen
| Zeile 32: | Zeile 32: | ||
<br> | <br> | ||
| − | 8. Färbe | + | 8. Färbe h<sub>c</sub> rot ein. ''Rechte Maustaste: Eigenschaften: Farbe'' |
<br> | <br> | ||
| − | 9. Konstruiere | + | 9. Konstruiere h<sub>a</sub> und h<sub>b</sub> wie in den Schritten 2-8. |
Version vom 23. September 2010, 20:03 Uhr
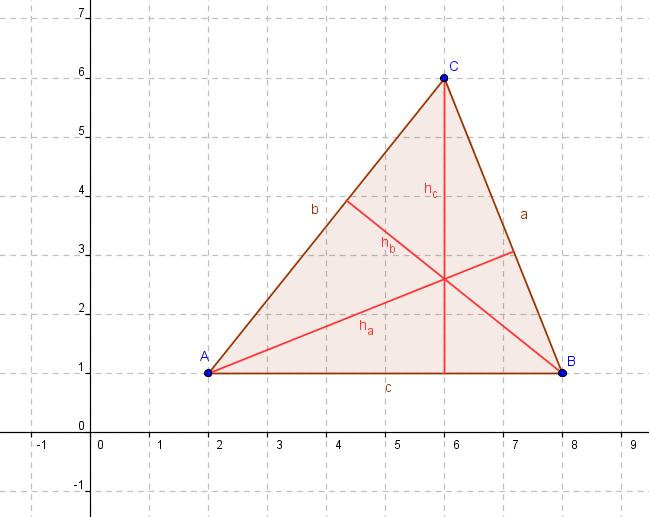
Die Höhen im Dreieck
Arbeitsaufträge:
- Folge der Konstruktionsbeschreibung, um ein Dreieck und die hc mit GeoGebra zu konstruieren.
- Konstruiere nur mit Hilfe von GeoGebra die Höhen ha und hb.
- Vergleiche deine Konstruktion mit der Lösung.
Konstruktionsbeschreibung:
1. Konstruiere ein Dreieck mit A(2|1), B(8|1) und C(6|6). Verwende dazu den Button Vieleck. 
2. Zeichne eine senkrechte Gerade d von der Strecke c durch den Punkt C. Klicke dazu auf den Button Senkrechte Gerade 
und dann auf die Strecke c und den Punkt C.
3. Schneide die Strecke c mit der Geraden d. Verwende dazu den Button Schneide zwei Objekte. 
4. Verstecke die Gerade d. Rechte Maustaste: Objekt anzeigen
5. Zeichne eine Strecke von C zu D mit dem Button Strecke zwischen zwei Punkten. 
6. Verstecke den Punkt D. Rechte Maustaste: Objekt anzeigen
7. Nenne die Strecke e in h_c um. Rechte Maustaste: Umbenennen
8. Färbe hc rot ein. Rechte Maustaste: Eigenschaften: Farbe
9. Konstruiere ha und hb wie in den Schritten 2-8.
Jede Seite des Dreiecks hat eine zugehörige Höhe, somit hat ein Dreieck drei Höhen.
Beim Dreieck muss nicht immer c die Grundlinie sein.
Wie berechnest du den Flächeninhalt, wenn...
...a und ha gegeben sind?
...b und hb gegeben sind?
Lösung:
- A
a
ha : 2
- Abhb : 2
Flächenformel für das Dreieck: ADreieck (GrundlinieHöheGrundlinie) : 2
Hier kommst du zu weiteren Übungsaufgaben.
