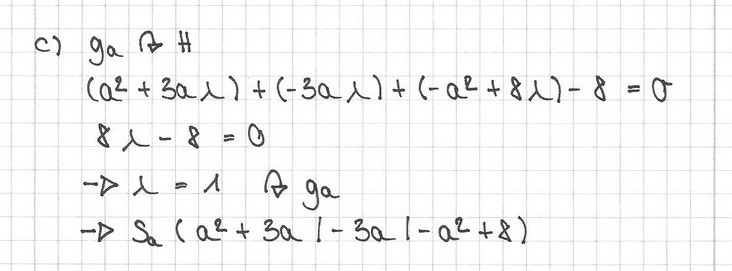2003 V: Unterschied zwischen den Versionen
| (4 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
| − | <center>[http://www.isb.bayern.de/isb/index.aspx?MNav=0&QNav=11&TNav=0&INav=0&VTyp=6&Fach=30&VJg=13 '''Download der Originalaufgaben: Abitur 2003 LK Mathematik Bayern'''] - [[Media:LKM Abi 2003 | + | <center>[http://www.isb.bayern.de/isb/index.aspx?MNav=0&QNav=11&TNav=0&INav=0&VTyp=6&Fach=30&VJg=13 '''Download der Originalaufgaben: Abitur 2003 LK Mathematik Bayern'''] - [[Media:LKM Abi 2003 VI lös.pdf|Lösung gesamt]]</center> |
| Zeile 69: | Zeile 69: | ||
<div align="right"><i>'''9 BE'''</i></div> | <div align="right"><i>'''9 BE'''</i></div> | ||
<br> | <br> | ||
| − | :{{Lösung versteckt|[[Bild:Mainberger_Lea_2003_V_1d_1.jpg]] | + | :{{Lösung versteckt|[[Bild:Mainberger_Lea_2003_V_1d_1.jpg]][[Bild:Mainberger_Lea_2003_V_1d_2.jpg]] |
}} | }} | ||
| Zeile 79: | Zeile 79: | ||
<div align="right"><i>'''8 BE'''</i></div> | <div align="right"><i>'''8 BE'''</i></div> | ||
<br> | <br> | ||
| − | :{{Lösung versteckt| | + | :{{Lösung versteckt|[[Bild:Mainberger_Lea_2003_V_1e.jpg]] |
}} | }} | ||
| Zeile 101: | Zeile 101: | ||
<div align="right"><i>'''5 BE'''</i></div> | <div align="right"><i>'''5 BE'''</i></div> | ||
<br> | <br> | ||
| − | :{{Lösung versteckt| | + | :{{Lösung versteckt|[[Bild:Mainberger_Lea_2003_V_2a.jpg]] |
}} | }} | ||
| Zeile 111: | Zeile 111: | ||
<div align="right"><i>'''6 BE'''</i></div> | <div align="right"><i>'''6 BE'''</i></div> | ||
<br> | <br> | ||
| − | :{{Lösung versteckt| | + | :{{Lösung versteckt|[[Bild:Mainberger_Lea_2003_V_2b.jpg]] |
}} | }} | ||
Aktuelle Version vom 22. April 2010, 17:46 Uhr
|
|
|
In einem kartesischen Koordinatensystem des
|
a) Zeigen Sie, dass keine der Geraden ga parallel und keine senkrecht zur Ebene H verläuft. 3 BE
b) Welche dieser Geraden schneidet H unter dem größten Winkel? Berechnen Sie diesen maximalen Winkel auf eine Dezimale genau. 6 BE
[ Zur Kontrolle: Sa = (a2 + 3a / -3a / 8 - a2) ] 3 BE
9 BE
8 BE
|
Ferner sind die Punkte A ( 1 / 6 / 1) und B (-2 / 9 / 1) gegeben.
5 BE
6 BE
|
 3 ist die
Ebene H: x1 + x2 + x3 - 8 = 0 , sowie die Schar von Geraden ga :
3 ist die
Ebene H: x1 + x2 + x3 - 8 = 0 , sowie die Schar von Geraden ga : 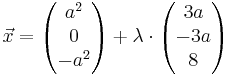 ,
, 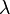 ∈
∈