2006 I: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
 
(17 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt)
Zeile 9: Zeile 9:
  
  
−
<center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=6765c5a90ce67dce2877992c3f4e2d9f '''Download der Originalaufgaben: Abitur 2008 LK Mathematik Bayern''']  -  [[Media:LKM Abi 2006 I lös.doc|Lösung gesamt]]</center>
+
<center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=ff574c530ac05ed359667c29b75a15ff '''Download der Originalaufgaben: Abitur 2006 LK Mathematik Bayern''']  -  [[Media:LKM Abi 2006 I lös.pdf|Lösung gesamt]]</center>
  
  
Zeile 26: Zeile 26:
 
;Aufgabe 1
 
;Aufgabe 1
  
 +
Gegeben ist die Funktion f: x→(x-1)<math>\cdot</math>lnx  mit der Definitionsmenge D=<math>\mathbb{R}</math><sup>+</sup>. Der Graph von f wird mit G<sub>f</sub>  bezeichnet. <br />
 +
Hinweis: <math>\lim_{x\to 0+} (x^n \cdot lnx)=0</math> für n <math>\in \mathbb{N}</math> , darf ohne Beweis verwendet werden. <br /> <br />
  
 +
;a) Geben Sie die Nullstelle von f an und untersuchen Sie das Verhalten von f an den Rändern der Definitionsmenge.
  
 
:{{Lösung versteckt|
 
:{{Lösung versteckt|
 +
[[Bild:Abi_2006_I_Lösung_1a.png|700px]]
 +
}}
 +
<div align="right">3 BE</div>
 +
<br />
  
 +
;b) Weisen Sie nach, dass G<sub>f</sub>  an der Stelle x=1  einen Punkt mit waagrechter Tangente besitzt. Bestimmen Sie das Monotonieverhalten von f. <br />
 +
:::[Zur Kontrolle: <math>f'(x)=lnx+1-{1 \over x}</math>] <br />
 +
 +
:{{Lösung versteckt|
 +
[[Bild:Abi_2006_I_Lösung_1b.png|700px]]
 
}}
 
}}
 +
<div align="right">5 BE</div>
 +
<br />
 +
 +
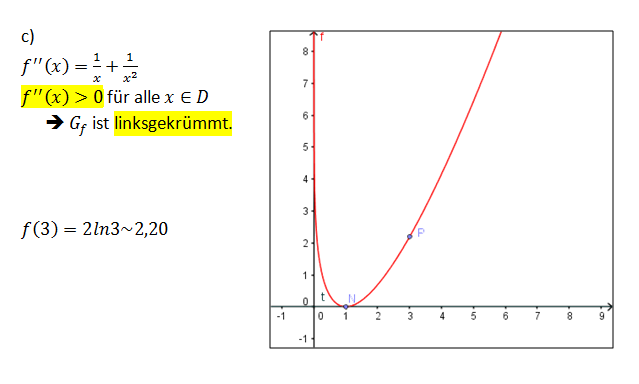
;c) Untersuchen Sie das Krümmungsverhalten von G<sub>f</sub> . Berechnen Sie f(3)  und skizzieren Sie  G<sub>f</sub> aufgrund der bisherigen Ergebnisse. <br />
 +
 +
:{{Lösung versteckt|
 +
[[Bild:Abi_2006_I_Lösung_1c.png|700px]]
 +
}}
 +
<div align="right">5 BE</div>
 +
<br />
 +
 +
;d) Begründen Sie, dass f im Intervall ]0;1]  umkehrbar ist. Geben Sie Definitions- und Wertemenge der zugehörigen Umkehrfunktion g an. <br />
 +
;Bestimmen Sie <math>\lim_{x\to0+}g'(x)</math> . <br />
 +
 +
:{{Lösung versteckt|
 +
[[Bild:Abi_2006_I_Lösung_1d_neu.png|700px]]
 +
}}
 +
<div align="right">4 BE</div>
 +
<br />
 +
 +
;e) G<sub>f</sub>  und die Koordinatenachsen begrenzen für x<math>\le</math>1  ein Flächenstück, das sich ins Unendliche erstreckt. Zeigen Sie, dass dieses Flächenstück den endlichen Inhalt 0,75 hat. <br />
 +
 +
:{{Lösung versteckt|
 +
[[Bild:Abi_2006_I_Lösung_1e_neu.png|700px]]
 +
}}
 +
<div align="right">8 BE</div>
 +
<br />
  
  
Zeile 44: Zeile 83:
  
 
;Aufgabe 2  
 
;Aufgabe 2  
 +
{|
 +
! width="400" |
 +
! width="100" |
 +
|-
 +
| valign="top" |
 +
Aus rechteckigen Kunststoffplatten von 1 Meter Breite und 2 Meter Höhe wurden Stücke abgeschnitten, wobei die Schnittkurve p<sub>t</sub>  Teil einer Parabel ist, die der Gleichung y=tx<sup>2</sup>+2-t  genügt. Für den Parameter t gilt: <math>0<t\le2</math> . In nebenstehender  Skizze ist der Fall t=1,6  dargestellt.
  
 +
|
 +
| valign="top" |
 +
[[Bild:Abi_2006_I_2_Graph_y.png|300px]]
  
 +
|}
  
  
 +
;a) Zeigen Sie, dass jede Schnittkurve p<sub>t</sub>  durch den Punkt (1/2) verläuft. Beschreiben Sie die Bewegung des Parabelscheitels, wenn t bei 2 beginnend alle Werte des Intervalls ]0;2] durchläuft.
  
 +
:{{Lösung versteckt|
 +
'''Bemerkung:
 +
In der 2ten Zeile wurde für t 1 eingesetzt. Allerdings muss hier t stehen bleiben, nur für x wird 1 eingesetzt.-> ERLEDIGT'''
 +
[[Bild:Abi2006ILösung2aneu.jpeg|700px]]
 +
}}
 +
<div align="right">3 BE</div>
 +
<br /> <br />
 +
 +
;''Aus der Restplatte werden Rechtecke – wie in der Skizze schraffiert (markiert) dargestellt – ausgeschnitten. Je eine Seite des Rechtecks soll auf dem unteren bzw. auf dem rechten Rand der Platte zu liegen kommen, eine Ecke des Rechtecks soll auf der Schnittkurve liegen.'' <br /> <br />
 +
 +
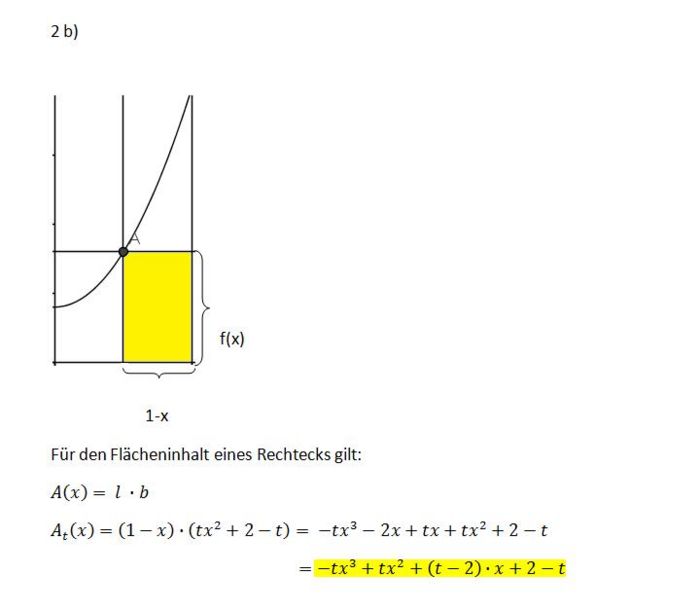
;b) Zeigen Sie, dass für den Inhalt eines solchen Rechtecks gilt:
 +
;A<sub>t</sub>(x)=-tx<sup>3</sup>+tx<sup>2</sup>+(t-2)x+2-t &nbsp;&nbsp; (0<math>\le</math>x<math>\le</math>1). <br />
 +
 +
:{{Lösung versteckt|
 +
[[Bild:Abi2006ILösung2b.jpeg|700px]]
 +
}}
 +
<div align="right">3 BE</div>
 +
<br />
 +
 +
;''Der Inhalt  des ausgeschnittenen Rechtecks soll möglichst groß sein (Extremwertproblem).'' <br /> <br />
 +
 +
;c) Die unten stehende Abbildung zeigt einige Graphen der Scharfunktionen A<sub>t</sub> . Beschreiben Sie, was aufgrund der Abbildung im Fall 0<t<1,5  für die Lösung des Extremwertproblems zu vermuten ist. <br />
 +
;Beweisen Sie Ihre Vermutung rechnerisch. <br />
 +
 +
<ggb_applet width="444" height="532"  version="3.2" ggbBase64="UEsDBBQACAAIACmbWDwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1spVZJb9s6ED63v4LgKWkRW4udxICVoq8PBQrktQd3AXpoQUljiw1FCiSVyP31b7jIS5oGXXIROTOc5Ztvxlm+GFpBbkEbrmRB00lCCchK1VxuCtrb9dklfXH1dLkBtYFSM7JWumW2oPkko07e86unT5amUXeECW/ykcNdQddMGKDEdBpYbRoAeyRn/cAFZ3r7rvwGlTV7RXDyRnY9RrG6R1nV1tfcjNepD9gJbv/lt7wGTYSqCno+x9Tx9BG05RUTBZ0lQZIVNLucHSlRlDttozT/rqR15nvna5QQYvh3wJeJky2nvtAl9JXgNWfSFePzQCNC7nhtGww4wygN8E2Duc7zJHirlNL1amsstGT4DFohzGnigN6G2yw9dzeDeWHAdLHwut31cpLg32IxW1zM84tZHrzC7QqsxS4ZwgYwI1QbzevD8xvzjxL1Dt1OcWlfsc722jc4j6KV3bpgGFe77F/KjYAoSxH/BqqbUg0rj0iaB9fvt51/4tMpN6+UUJpoRGw+R4P4LcPX27g8d1aJt0m8RfThnO706SLzFv5bhq+3ElyG1GLd+Vh0moxhuCFO4DBFXo5wCFYCtnmgpJfcXocbJciHm32p7sHbvi1xIA4ZsfOZPuhz+/s+l9N7XFregJYgAmMkdrZXvSG3jpmheT6RGire4jUoIiTMtesDJhCkNWw0jImHcQqAee0RK++Jl9MxCZeDwVwri3sB67GuFje2FkemoK+xS5g5+cTFDSU1s07r5kNACzg81nND9i1oXu1gstRFxnB9DJpOzuM4u/2h/Cq4B+2+B6j+CXtwaXQNw9MkjRxhW1wLh+V6b/+pegwcwwq/P1ouw2PSssFltUCXpVGit7CqEEt5rSpm/YYMycWBTxM/x/gmu7jwU4tzn7nDmg+wH7uH18yeybZBwkgwxrU0gjeyWWK/fRNwgXQxTdOB8+639WhNOqzaD/WOLsix0A/XmQE3sXFbfkT25Vf0hGJ/OhlOSUHOTuwpeUaGLyf5JDklz4kNtyzcTiw5I/6MUrzjEQWWkukPrV/30lOHHkb7adGze0Uf0SFi+Ed8SB7lw7v12oB17ZunvnfZ5YNsSR7p13Hqh4hXqm2ZrIlkLapfj4A4T9z9uhGWxCawNORKWBaaGurr7d7KBu/R56/Abf8Q7r+YvsfR/ls8p4cryf8kx/9Jrv4HUEsHCKUEDXx7AwAAxQgAAFBLAQIUABQACAAIACmbWDylBA18ewMAAMUIAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAtQMAAAAA" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" />
 +
 +
:{{Lösung versteckt|
 +
[[Bild:Abi2006ILösung2cneu.jpeg|700px]]
 +
}}
 +
<div align="right">6 BE</div>
 +
<br />
 +
 +
;d) Im Fall t=1,6  ist die erste Ableitung von A<sub>t</sub>  an den Stellen <math>x_1={1 \over 6}</math> und <math>x_2={1 \over 2}</math>  gleich Null <br />
 +
;(Nachweis nicht erforderlich). <br />
 +
;Bestätigen Sie durch Berechnung geeigneter Werte von A<sub>t</sub> , dass für t=1,6  zwei Rechtecke den maximalen Flächeninhalt aufweisen.
 +
 +
:{{Lösung versteckt|
 +
[[Bild:Abi2006ILösung2d.jpeg|700px]]
 +
}}
 +
<div align="right">3 BE</div>
 +
<br />
  
 
</td></tr></table></center>
 
</td></tr></table></center>

Aktuelle Version vom 5. April 2010, 20:35 Uhr


Leistungskurs Mathematik (Bayern): Abiturprüfung 2006
Infinitesimalrechnung I


Download der Originalaufgaben: Abitur 2006 LK Mathematik Bayern - Lösung gesamt


Erarbeitet von Lukas Baumüller, Florian Wilk


Aufgabe 1

Gegeben ist die Funktion f: x→(x-1)\cdotlnx mit der Definitionsmenge D=\mathbb{R}+. Der Graph von f wird mit Gf bezeichnet.
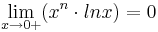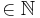Hinweis: \lim_{x\to 0+} (x^n \cdot lnx)=0 für n \in \mathbb{N} , darf ohne Beweis verwendet werden.

a) Geben Sie die Nullstelle von f an und untersuchen Sie das Verhalten von f an den Rändern der Definitionsmenge.

Abi 2006 I Lösung 1a.png

3 BE


b) Weisen Sie nach, dass Gf an der Stelle x=1 einen Punkt mit waagrechter Tangente besitzt. Bestimmen Sie das Monotonieverhalten von f.
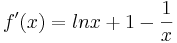[Zur Kontrolle: f'(x)=lnx+1-{1 \over x}]

Abi 2006 I Lösung 1b.png

5 BE


c) Untersuchen Sie das Krümmungsverhalten von Gf . Berechnen Sie f(3) und skizzieren Sie Gf aufgrund der bisherigen Ergebnisse.

Abi 2006 I Lösung 1c.png

5 BE


d) Begründen Sie, dass f im Intervall ]0;1] umkehrbar ist. Geben Sie Definitions- und Wertemenge der zugehörigen Umkehrfunktion g an.
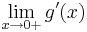Bestimmen Sie \lim_{x\to0+}g'(x) .

Abi 2006 I Lösung 1d neu.png

4 BE


e) Gf und die Koordinatenachsen begrenzen für x\le1 ein Flächenstück, das sich ins Unendliche erstreckt. Zeigen Sie, dass dieses Flächenstück den endlichen Inhalt 0,75 hat.

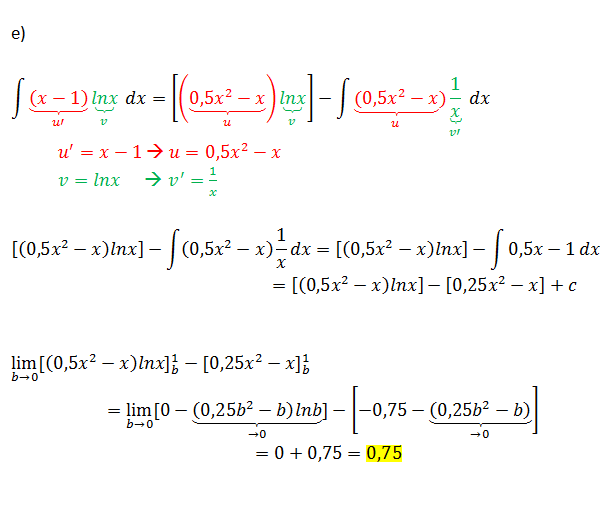
Abi 2006 I Lösung 1e neu.png

8 BE




Aufgabe 2

Aus rechteckigen Kunststoffplatten von 1 Meter Breite und 2 Meter Höhe wurden Stücke abgeschnitten, wobei die Schnittkurve pt Teil einer Parabel ist, die der Gleichung y=tx2+2-t genügt. Für den Parameter t gilt: 0<t\le2 . In nebenstehender Skizze ist der Fall t=1,6 dargestellt.

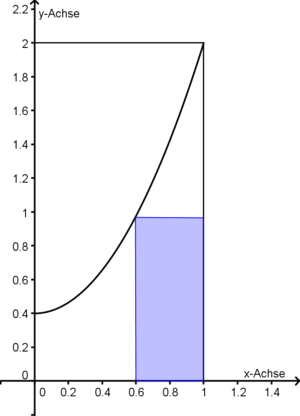
Abi 2006 I 2 Graph y.png


a) Zeigen Sie, dass jede Schnittkurve pt durch den Punkt (1/2) verläuft. Beschreiben Sie die Bewegung des Parabelscheitels, wenn t bei 2 beginnend alle Werte des Intervalls ]0;2] durchläuft.

Bemerkung: In der 2ten Zeile wurde für t 1 eingesetzt. Allerdings muss hier t stehen bleiben, nur für x wird 1 eingesetzt.-> ERLEDIGT Abi2006ILösung2aneu.jpeg

3 BE



Aus der Restplatte werden Rechtecke – wie in der Skizze schraffiert (markiert) dargestellt – ausgeschnitten. Je eine Seite des Rechtecks soll auf dem unteren bzw. auf dem rechten Rand der Platte zu liegen kommen, eine Ecke des Rechtecks soll auf der Schnittkurve liegen.

b) Zeigen Sie, dass für den Inhalt eines solchen Rechtecks gilt
At(x)=-tx3+tx2+(t-2)x+2-t    (0\lex\le1).

Abi2006ILösung2b.jpeg

3 BE


Der Inhalt des ausgeschnittenen Rechtecks soll möglichst groß sein (Extremwertproblem).

c) Die unten stehende Abbildung zeigt einige Graphen der Scharfunktionen At . Beschreiben Sie, was aufgrund der Abbildung im Fall 0<t<1,5 für die Lösung des Extremwertproblems zu vermuten ist.
Beweisen Sie Ihre Vermutung rechnerisch.

Abi2006ILösung2cneu.jpeg

6 BE


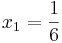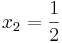d) Im Fall t=1,6 ist die erste Ableitung von At an den Stellen x_1={1 \over 6} und x_2={1 \over 2} gleich Null
(Nachweis nicht erforderlich).
Bestätigen Sie durch Berechnung geeigneter Werte von At , dass für t=1,6 zwei Rechtecke den maximalen Flächeninhalt aufweisen.

Abi2006ILösung2d.jpeg

3 BE



Von „http://rmg.zum.de/index.php?title=LK_Mathematik/Abitur/2006_I&oldid=31811“