2006 I: Unterschied zwischen den Versionen
Aus RMG-Wiki
< LK Mathematik | Abitur
| Zeile 26: | Zeile 26: | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
| + | Gegeben ist die Funktion f: x→(x-1)<math>\cdot</math>lnx mit der Definitionsmenge D=<math>\mathbb{R}</math><sup>+</sup>. Der Graph von f wird mit G<sub>f</sub> bezeichnet. <br /> | ||
| + | Hinweis: <math>\lim_{x\to 0+} (x^n \cdot lnx)=0</math> für n <math>\in \mathbb{N}</math> , darf ohne Beweis verwendet werden. <br /> <br /> | ||
| + | ;a) Geben Sie die Nullstelle von f an und untersuchen Sie das Verhalten von f an den Rändern der Definitionsmenge. | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| + | folgt demnächst ... | ||
| + | }} | ||
| + | <div align="right">3 BE</div> | ||
| + | <br /> | ||
| + | ;b) Weisen Sie nach, dass G<sub>f</sub> an der Stelle x=1 einen Punkt mit waagrechter Tangente besitzt. Bestimmen Sie das Monotonieverhalten von f. <br /> | ||
| + | :::[Zur Kontrolle: <math>f'(x)=lnx+1-{1 \over x}</math>] <br /> | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | folgt demnächst ... | ||
}} | }} | ||
| + | <div align="right">5 BE</div> | ||
| + | <br /> | ||
| + | |||
| + | ;c) Untersuchen Sie das Krümmungsverhalten von G<sub>f</sub> . Berechnen Sie f(3) und skizzieren Sie G<sub>f</sub> aufgrund der bisherigen Ergebnisse. <br /> | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | folgt demnächst ... | ||
| + | }} | ||
| + | <div align="right">5 BE</div> | ||
| + | <br /> | ||
| + | |||
| + | ;d) Begründen Sie, dass f im Intervall ]0;1] umkehrbar ist. Geben Sie Definitions- und Wertemenge der zugehörigen Umkehrfunktion g an. <br /> | ||
| + | ;Bestimmen Sie <math>\lim_{x\to0+}g'(x)</math> . <br /> | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | folgt demnächst ... | ||
| + | }} | ||
| + | <div align="right">4 BE</div> | ||
| + | <br /> | ||
| + | |||
| + | ;e) G<sub>f</sub> und die Koordinatenachsen begrenzen für x<math>\le</math>1 ein Flächenstück, das sich ins Unendliche erstreckt. Zeigen Sie, dass dieses Flächenstück den endlichen Inhalt 0,75 hat. <br /> | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | folgt demnächst ... | ||
| + | }} | ||
| + | <div align="right">8 BE</div> | ||
| + | <br /> | ||
| Zeile 44: | Zeile 83: | ||
;Aufgabe 2 | ;Aufgabe 2 | ||
| + | {| | ||
| + | ! width="400" | | ||
| + | ! width="100" | | ||
| + | |- | ||
| + | | valign="top" | | ||
| + | Aus rechteckigen Kunststoffplatten von 1 Meter Breite und 2 Meter Höhe wurden Stücke abgeschnitten, wobei die Schnittkurve p<sub>t</sub> Teil einer Parabel ist, die der Gleichung y=tx<sup>2</sup>+2-t genügt. Für den Parameter t gilt: <math>0<t\le2</math> . In nebenstehender Skizze ist der Fall t=1,6 dargestellt. | ||
| + | | | ||
| + | | valign="top" | | ||
| + | [[Bild:Abi_2006_I_2_Graph.jpg|300px]] | ||
| + | |} | ||
| + | ;a) Zeigen Sie, dass jede Schnittkurve p<sub>t</sub> durch den Punkt (1/2) verläuft. Beschreiben Sie die Bewegung des Parabelscheitels, wenn t bei 2 beginnend alle Werte des Intervalls ]0;2] durchläuft. | ||
| + | :{{Lösung versteckt| | ||
| + | folgt demnächst ... | ||
| + | }} | ||
| + | <div align="right">3 BE</div> | ||
| + | <br /> <br /> | ||
| + | |||
| + | ;''Aus der Restplatte werden Rechtecke – wie in der Skizze schraffiert dargestellt – ausgeschnitten. Je eine Seite des Rechtecks soll auf dem unteren bzw. auf dem rechten Rand der Platte zu liegen kommen, eine Ecke des Rechtecks soll auf der Schnittkurve liegen.'' <br /> <br /> | ||
| + | |||
| + | ;b) Zeigen Sie, dass für den Inhalt eines solchen Rechtecks gilt: | ||
| + | ;A<sub>t</sub>(x)=-tx<sup>3</sup>+tx<sup>2</sup>+(t-2)x+2-t (0<math>\le</math>x<math>\le</math>1). <br /> | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | folgt demnächst ... | ||
| + | }} | ||
| + | <div align="right">3 BE</div> | ||
| + | <br /> | ||
| + | |||
| + | ;''Der Inhalt des ausgeschnittenen Rechtecks soll möglichst groß sein (Extremwertproblem).'' <br /> <br /> | ||
| + | |||
| + | ;c) Die unten stehende Abbildung zeigt einige Graphen der Scharfunktionen A<sub>t</sub> . Beschreiben Sie, was aufgrund der Abbildung im Fall 0<t<1,5 für die Lösung des Extremwertproblems zu vermuten ist. <br /> | ||
| + | ;Beweisen Sie Ihre Vermutung rechnerisch. <br /> | ||
| + | |||
| + | [[Bild:Abi_2006_I_2c_Graph.jpg|500px]] | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | folgt demnächst ... | ||
| + | }} | ||
| + | <div align="right">6 BE</div> | ||
| + | <br /> | ||
| + | |||
| + | ;d) Im Fall t=1,6 ist die erste Ableitung von A<sub>t</sub> an den Stellen <math>x_1={1 \over 6}</math> und <math>x_2={1 \over 2}</math> gleich Null <br /> | ||
| + | ;(Nachweis nicht erforderlich). <br /> | ||
| + | ;Bestätigen Sie durch Berechnung geeigneter Werte von A<sub>t</sub> , dass für t=1,6 zwei Rechtecke den maximalen Flächeninhalt aufweisen. | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | folgt demnächst ... | ||
| + | }} | ||
| + | <div align="right">3 BE</div> | ||
| + | <br /> | ||
</td></tr></table></center> | </td></tr></table></center> | ||
Version vom 20. Februar 2010, 21:12 Uhr
|
|
Gegeben ist die Funktion f: x→(x-1)
3 BE
5 BE
5 BE
4 BE
8 BE
|
3 BE
3 BE
6 BE
3 BE
|
 lnx mit der Definitionsmenge D=
lnx mit der Definitionsmenge D= +. Der Graph von f wird mit Gf bezeichnet.
+. Der Graph von f wird mit Gf bezeichnet. 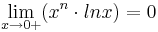 für n
für n 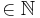 , darf ohne Beweis verwendet werden.
, darf ohne Beweis verwendet werden. 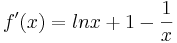 ]
] 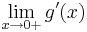 .
.  1 ein Flächenstück, das sich ins Unendliche erstreckt. Zeigen Sie, dass dieses Flächenstück den endlichen Inhalt 0,75 hat.
1 ein Flächenstück, das sich ins Unendliche erstreckt. Zeigen Sie, dass dieses Flächenstück den endlichen Inhalt 0,75 hat. 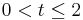 . In nebenstehender Skizze ist der Fall t=1,6 dargestellt.
. In nebenstehender Skizze ist der Fall t=1,6 dargestellt.
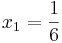 und
und 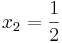 gleich Null
gleich Null 
