2006 I: Unterschied zwischen den Versionen
Aus RMG-Wiki
< LK Mathematik | Abitur
(musterseite eingefügt) |
|||
| Zeile 26: | Zeile 26: | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
| + | a) Untersuchen Sie das Verhalten <math>f_k \,</math> <math>x \rightarrow +\infty</math> und <math>x \rightarrow -\infty</math>. | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| Zeile 31: | Zeile 32: | ||
}} | }} | ||
| + | b) Bestimmen Sie das Monotonieverhalten von <math>f_k \,</math> und geben Sie die Wertemenge an. | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | |||
| + | }} | ||
| + | |||
| + | c) Weisen Sie nach, dass der Punkt <math>W_k ( 0/ \frac{k}{2} )</math> der einzige Wendepunkt von G_k ist. | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | |||
| + | }} | ||
| + | |||
| + | d) Weisen Sie nach, dass für alle <math>k \in R^{+}</math> und <math>x \in R</math> gilt:<br /> | ||
| + | : <math>f_k(-x) + f_k(x) = k \,</math>. Begründen Sie damit die Symmetrie von <math>G_k \,</math> zum Punkt <math>W_k \,</math>. | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | |||
| + | }} | ||
Version vom 18. Februar 2010, 15:45 Uhr
|
|
a) Untersuchen Sie das Verhalten b) Bestimmen Sie das Monotonieverhalten von c) Weisen Sie nach, dass der Punkt d) Weisen Sie nach, dass für alle
|
|
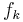
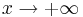 und
und 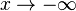 .
.
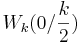 der einzige Wendepunkt von G_k ist.
der einzige Wendepunkt von G_k ist.
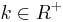 und
und 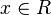 gilt:
gilt: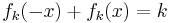 . Begründen Sie damit die Symmetrie von
. Begründen Sie damit die Symmetrie von 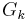 zum Punkt
zum Punkt 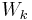 .
.

