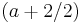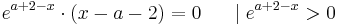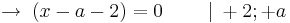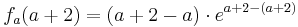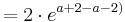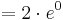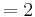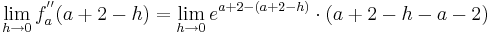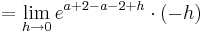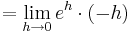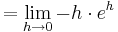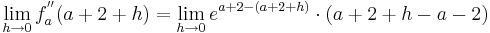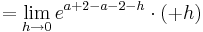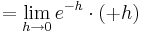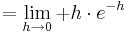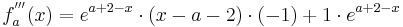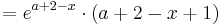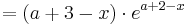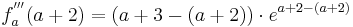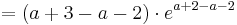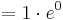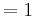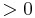Lösung: Wendepunkte: Unterschied zwischen den Versionen
(→Überprüfung des Wendepunkts) |
(→1. Möglichkeit; H-Methode) |
||
| (5 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
Um mögliche Wendepunkte zu bestimmen benötigt man die zweite Ableitung. | Um mögliche Wendepunkte zu bestimmen benötigt man die zweite Ableitung. | ||
| − | Die zweite Ableitung einer Funktion beschreibt das Krümmungsverhalten dieser. Dieses ändert sich für <math>f_a^{''} (x) = 0\;</math> und | + | Die zweite Ableitung einer Funktion beschreibt das Krümmungsverhalten dieser. Dieses ändert sich für <math>f_a^{''} (x) = 0\;</math> und deshalb könnte ein möglicher Wendepunkt auftreten. |
| Zeile 18: | Zeile 18: | ||
| − | Möglicher Wendepunkt bei <math>x = a + 2 \; </math> | + | Möglicher Wendepunkt bei <math>x = a + 2 \; </math><br /> |
| + | Einsetzen des möglichen Wendepunkts in die Funktion. | ||
| Zeile 38: | Zeile 39: | ||
Wenn es einen Vorzeichenwechsel (VZW) des Krümmungsverhaltens der Funktion am möglichen Wendepunkt gibt, kann man von einem Wendepunkt sprechen. | Wenn es einen Vorzeichenwechsel (VZW) des Krümmungsverhaltens der Funktion am möglichen Wendepunkt gibt, kann man von einem Wendepunkt sprechen. | ||
| + | |||
| + | '''I.<br />''' | ||
: <math>\lim_{h\to 0}f_a^{''} ( a + 2 - h ) = \lim_{h\to 0}e^{a + 2 - (a + 2 - h )}\cdot ( a + 2 - h - a - 2 )</math><br /> | : <math>\lim_{h\to 0}f_a^{''} ( a + 2 - h ) = \lim_{h\to 0}e^{a + 2 - (a + 2 - h )}\cdot ( a + 2 - h - a - 2 )</math><br /> | ||
::::::: <math>=\lim_{h\to 0} e^{a + 2 - a- 2 + h }\cdot (- h)</math><br /> | ::::::: <math>=\lim_{h\to 0} e^{a + 2 - a- 2 + h }\cdot (- h)</math><br /> | ||
::::::: <math>= \lim_{h\to 0}e^{h }\cdot ( -h )</math><br /> | ::::::: <math>= \lim_{h\to 0}e^{h }\cdot ( -h )</math><br /> | ||
::::::: <math>= \lim_{h\to 0}-h\cdot e^{h }</math><br /> | ::::::: <math>= \lim_{h\to 0}-h\cdot e^{h }</math><br /> | ||
| − | + | <math>\lim_{h\to 0}f_a^{''} ( a + 2 - h )<0</math> | |
| − | + | <math>\rightarrow</math> An der Stelle <math>\lim_{h\to 0}f_a^{''}( a +2+ h )\;</math> ist der Graph linksgekrümmt.(I) | |
| + | '''II.'''<br /> | ||
: <math>\lim_{h\to 0}f_a^{''} ( a + 2 + h ) =\lim_{h\to 0} e^{a + 2 - (a + 2 + h )}\cdot ( a + 2 + h - a - 2 )</math><br /> | : <math>\lim_{h\to 0}f_a^{''} ( a + 2 + h ) =\lim_{h\to 0} e^{a + 2 - (a + 2 + h )}\cdot ( a + 2 + h - a - 2 )</math><br /> | ||
::::::: <math>=\lim_{h\to 0} e^{a + 2 - a- 2 - h }\cdot (+ h)</math><br /> | ::::::: <math>=\lim_{h\to 0} e^{a + 2 - a- 2 - h }\cdot (+ h)</math><br /> | ||
::::::: <math>= \lim_{h\to 0}e^{-h }\cdot ( +h )</math><br /> | ::::::: <math>= \lim_{h\to 0}e^{-h }\cdot ( +h )</math><br /> | ||
::::::: <math>= \lim_{h\to 0}+h\cdot e^{-h }</math><br /> | ::::::: <math>= \lim_{h\to 0}+h\cdot e^{-h }</math><br /> | ||
| − | + | <math>\lim_{h\to 0}f_a^{''} ( a + 2 + h )>0</math> | |
| − | + | <math>\rightarrow</math> An der Stelle <math>\lim_{h\to 0}f_a^{'}(a+2-h )\;</math> ist der Graph rechtsgekrümmt.(II) | |
| Zeile 61: | Zeile 65: | ||
| − | <u>zur Verdeutlichung</u> | + | <u>zur Verdeutlichung:</u> |
{| class="wikitable centersortable" | {| class="wikitable centersortable" | ||
| Zeile 135: | Zeile 139: | ||
:::: <math>= 1\cdot e^{0}</math><br /> | :::: <math>= 1\cdot e^{0}</math><br /> | ||
:::: <math>= 1\;</math><br /> | :::: <math>= 1\;</math><br /> | ||
| − | :::: <math>> 0\;</math> | + | :::: <math>> 0\;</math><br /> |
| + | |||
<math>\rightarrow</math> WP <math>( a + 2 / 2 )\;</math> | <math>\rightarrow</math> WP <math>( a + 2 / 2 )\;</math> | ||
Aktuelle Version vom 26. Januar 2010, 19:43 Uhr
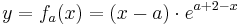 mit
mit 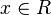 ;
; 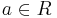
Inhaltsverzeichnis |
Wendepunkte
Zweite Ableitung: siehe Überprüfung des Extrempunkts; 2. Möglichkeit
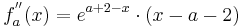
Um mögliche Wendepunkte zu bestimmen benötigt man die zweite Ableitung.
Die zweite Ableitung einer Funktion beschreibt das Krümmungsverhalten dieser. Dieses ändert sich für 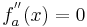 und deshalb könnte ein möglicher Wendepunkt auftreten.
und deshalb könnte ein möglicher Wendepunkt auftreten.
Möglicher Wendepunkt bei 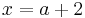
Einsetzen des möglichen Wendepunkts in die Funktion.
 mög. WP
mög. WP 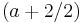
Überprüfung des Wendepunkts
1. Möglichkeit; H-Methode
Wenn es einen Vorzeichenwechsel (VZW) des Krümmungsverhaltens der Funktion am möglichen Wendepunkt gibt, kann man von einem Wendepunkt sprechen.
I.
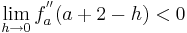
 An der Stelle
An der Stelle 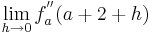 ist der Graph linksgekrümmt.(I)
ist der Graph linksgekrümmt.(I)
II.
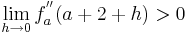
 An der Stelle
An der Stelle 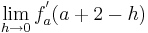 ist der Graph rechtsgekrümmt.(II)
ist der Graph rechtsgekrümmt.(II)
Aus (I) und (II) folgt:
VZW bei 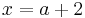
 Wendepunkt bei
Wendepunkt bei 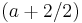
zur Verdeutlichung:
| x<2+a | x=2+a | x>2+a | |||
|---|---|---|---|---|---|
| ea + 2 - x | + | + | |||
| ( x - a - 2 ) | - | + | |||
| fa ( x ) | - | + |
 WP
WP 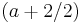
2. Möglichkeit; 3.Ableitung
Verwendung der dritten Ableitung
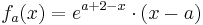
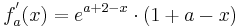
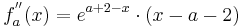
Um die dritte Ableitung zu bekommen muss man hier die Produktregel verwenden.
[Hilfe zur Produktregel]
Wenn die dritte Ableitung am möglichen Wendepunkt ungleich Null ist, liegt ein Wendepunkt vor.
 WP
WP