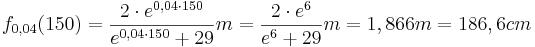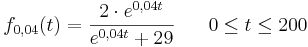Lösung d): Unterschied zwischen den Versionen
Aus RMG-Wiki
K (Die Seite wurde neu angelegt: Durch die Funktion <math>f_{0,04}\;</math> für <math>0\leq t\leq 200</math> (t in Tagen) kann das Wachstum von Sonnenblumen beschrieben werden, wobei <math>f_{0,04} (t...) |
K (→Berechnen Sie die Höhe einer Sonnenblumenpflanze nach 10, 50 und 150 Tagen) |
||
| Zeile 4: | Zeile 4: | ||
===<u>Berechnen Sie die Höhe einer Sonnenblumenpflanze nach 10, 50 und 150 Tagen</u>=== | ===<u>Berechnen Sie die Höhe einer Sonnenblumenpflanze nach 10, 50 und 150 Tagen</u>=== | ||
| + | <br /> | ||
| + | '''Höhe nach 10 Tagen:''' | ||
| + | <math>f_{0,04} (10) = \frac {2\cdot e^{0,04\cdot 10}} {e^{0,04\cdot 10} + 29} m = \frac {2\cdot e^{0,4}} {e^{0,4} + 29} m = 0,098m = 9,8cm</math> | ||
| + | '''Höhe nach 50 Tagen:''' | ||
| + | <math>f_{0,04} (50) = \frac {2\cdot e^{0,04\cdot 50}} {e^{0,04\cdot 50} + 29} m = \frac {2\cdot e^{2}} {e^{2} + 29} m = 0,406m = 40,6cm</math> | ||
| + | |||
| + | '''Höhe nach 150 Tagen:''' | ||
| + | |||
| + | <math>f_{0,04} (150) = \frac {2\cdot e^{0,04\cdot 150}} {e^{0,04\cdot 150} + 29} m = \frac {2\cdot e^{6}} {e^{6} + 29} m = 1,866m = 186,6cm</math> | ||
===<u>Berechnen Sie, wann die Wachstumsgeschwindigkeit einer Sonnenblumenpflanze am größten ist</u>=== | ===<u>Berechnen Sie, wann die Wachstumsgeschwindigkeit einer Sonnenblumenpflanze am größten ist</u>=== | ||
Version vom 25. Januar 2010, 20:33 Uhr
Durch die Funktion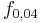 
für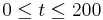 
(t in Tagen) kann das Wachstum von Sonnenblumen beschrieben werden, wobei 
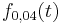die Höhe (in m) der Pflanzen zur Zeit t bedeutet.
Berechnen Sie die Höhe einer Sonnenblumenpflanze nach 10, 50 und 150 Tagen
Höhe nach 10 Tagen:
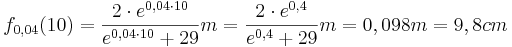
Höhe nach 50 Tagen:
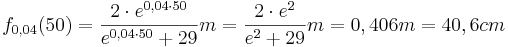
Höhe nach 150 Tagen:
