Teilaufgabe a: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 25: | Zeile 25: | ||
Graph der Funktion <math>f_2\,</math> für <math>1,6 \le x \le 7</math> | Graph der Funktion <math>f_2\,</math> für <math>1,6 \le x \le 7</math> | ||
| − | <ggb_applet width=" | + | <ggb_applet width="270" height="498" version="3.2" ggbBase64="UEsDBBQACAAIAN2zNzwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1srVVNb9swDD2vv0LQqR3QxHaSNgXsFlt3KbCPQ7Yedtgg24ytVZYCSU6d/vpRkp04GQpswA6FLJIhHx8f1fSuawTZgjZcyYzGk4gSkIUquawy2tr15ZLe3Z6lFagKcs3IWumG2YzOJgl19pbfnr1JTa2eCRM+5JHDc0bXTBigxGw0sNLUAPbIztqOC8707kv+CwprDo6Q5EFuWqxidYu2oik/cjNcp77gRnD7gW95CZoIVWT0aoHQ8esRtOUFExmdR8GSZDQ5caJp5ry10vxFSevCD8nXaCHE8BdARhJnS6e+0RTaQvCSM+ma8TgwiJBnXtoaq1y7lMCrGrHOb65CtkIpXa52xkJDuu+gVUYvl5EjehduyfzK3QziwoKL4BrffBrYrsBaHIshrAMzcFNpXu7Jc5cH816Jg2mjuLT3bGNb7Uc6600ru3P5sZR2eN/JSkBvS5DxGoqnXHWrwMEspP662/ifeDx5da+E0kQ7dhcY0J95OH2MA7qPinxM5CP6HC7p3h/fJD7Cn3k4fZTgMkDrG4+HruNoKMMNcQbHIipx4EawHHCwlLSS24/DBQXw1Hcah/jPbZPjBowlsE8Z/6eU6fREO+kTaAkiKETiYFvVGrJ1Sgyj8zhKKHiD1+DoCWFuWN8QQLCWUGkYcIf1CXR5bzRW4Yk5nQ4gHAaDWAuL7wD2Y10vbk0troj7Kpl1FrcDAhrABbFeDbJtQPNizwxQVw1LtH2hZHIdL5Ol+5svbqJ5Lw3/Yii//Hut9ikOU0D/K/LBd2JTM/yaxL1I2A5fgnHHPtsnVfY4+rg176AMltG0h9fo2IEzC726rjt8yYx7JQeY65+oUzT7r/PugmTkvCOXJJlEF+QtgR/n80mE9+6CkukfvK1b6bmm43THarc1ykpiUb+Sdrx8R+wdKfPfyIv+krzodBNfxTbmbDoWlX9E+/8it78BUEsHCEYGSLbKAgAAdwYAAFBLAQIUABQACAAIAN2zNzxGBki2ygIAAHcGAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAABAMAAAAA" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> |
}}<br /> | }}<br /> | ||
Version vom 23. Januar 2010, 22:31 Uhr
Für jede reelle Zahl a sei eine Funktion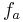 
durch 
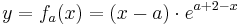mit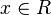 
gegeben.
- 1.Untersuchen Sie den Graphen von 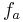auf:
- Schnittpunkte mit den Koordinatenachsen,
Lösung: Schnittpunkte mit den Koordinatenachsen - lokale Extrempunkte und
Lösung: lokale Extrempunkte - Wendepunkte!
Lösung: Wendepunkte
- Schnittpunkte mit den Koordinatenachsen,
- Bestimmen Sie gegebenenfalls deren Koordinaten!
- 2.Alle Extrempunkte liegen auf dem Graphen einer Funktion h. Geben Sie eine Funktionsgleichung von h an!
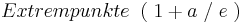
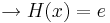
Alle Extrempunkte für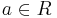 
befinde sich auf einer Parallelen zur x-Achse mit 
.
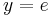Das heißt, dass alle Extrempunkte auf dem Graphen der Funktion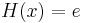 
liegen.
- 3.Skizzieren Sie den Graphen der Funktion
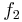für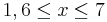 
!
Graph der Funktion 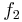für
