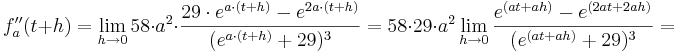Lösung b): Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(→‎Suche nach dem Wendepunkt:)
(→‎Untersuchen sie die Funktionen fa auf Nullstellen und lokale Extremstellen)
Zeile 10: Zeile 10:
 
<math>\Rightarrow e^{at} = 0 (f)</math><br />
 
<math>\Rightarrow e^{at} = 0 (f)</math><br />
  
−
<math>\Rightarrow</math> keine Nullstellen, da die e-Fkt. nie 0 wird und somit der Ausdruck <math>e^{at}</math> ebenfalls nie 0 werden kann
+
<math>\Rightarrow</math> keine Nullstellen, da die e-Fkt. nie 0 wird und somit der Ausdruck <math>e^{at}\;</math> ebenfalls nie 0 werden kann
  
 
===<u>Suche nach Extremstellen:</u>===
 
===<u>Suche nach Extremstellen:</u>===
Zeile 16: Zeile 16:
 
<math>f'_{a} (t) = \frac{58\cdot a\cdot e^{at} }{(e^{at}+29) ^{2}} = 0 \Rightarrow 58\cdot a \cdot e^{at} = 0 \Rightarrow e^{at} = 0 (f)</math>
 
<math>f'_{a} (t) = \frac{58\cdot a\cdot e^{at} }{(e^{at}+29) ^{2}} = 0 \Rightarrow 58\cdot a \cdot e^{at} = 0 \Rightarrow e^{at} = 0 (f)</math>
  
−
<math>\Rightarrow</math> keine Extremstellen, da die e-Fkt. nie 0 wird und somit der Ausdruck <math>e^{at}</math> ebenfalls nie 0 werden kann
+
<math>\Rightarrow</math> keine Extremstellen, da die e-Fkt. nie 0 wird und somit der Ausdruck <math>e^{at}\;</math> ebenfalls nie 0 werden kann
−
 
+
  
 
==Jeder Graph G<sub>a</sub> bestitzt genau einen Wendepunkt W<sub>a</sub>. Zeigen sie, dass die Wendepunkte W<sub>a</sub> auf einer parallelen zur t-Achse liegen==
 
==Jeder Graph G<sub>a</sub> bestitzt genau einen Wendepunkt W<sub>a</sub>. Zeigen sie, dass die Wendepunkte W<sub>a</sub> auf einer parallelen zur t-Achse liegen==

Version vom 16. Januar 2010, 10:16 Uhr

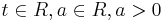
y = f_{a}(t) = \frac{2\cdot e^{at}}{e^{at}+29}, t\in R, a\in R, a>0

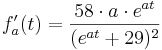
f'_{a} (t) = \frac{58\cdot a\cdot e^{at} }{(e^{at}+29) ^{2}}

Inhaltsverzeichnis

Untersuchen sie die Funktionen fa auf Nullstellen und lokale Extremstellen

Suche nach Nullstellen:

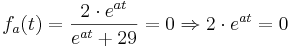
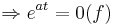
f_{a}(t) = \frac{2\cdot e^{at}}{e^{at}+29} = 0 \Rightarrow 2\cdot e^{at} = 0 \Rightarrow e^{at} = 0 (f)

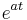\Rightarrow keine Nullstellen, da die e-Fkt. nie 0 wird und somit der Ausdruck e^{at}\; ebenfalls nie 0 werden kann

Suche nach Extremstellen:

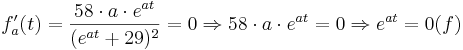
f'_{a} (t) = \frac{58\cdot a\cdot e^{at} }{(e^{at}+29) ^{2}} = 0 \Rightarrow 58\cdot a \cdot e^{at} = 0 \Rightarrow e^{at} = 0 (f)

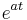\Rightarrow keine Extremstellen, da die e-Fkt. nie 0 wird und somit der Ausdruck e^{at}\; ebenfalls nie 0 werden kann

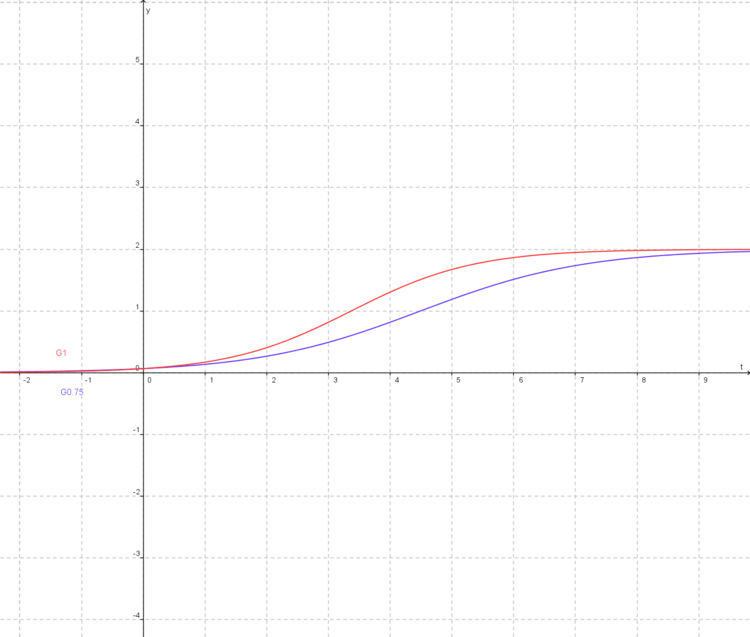
Jeder Graph Ga bestitzt genau einen Wendepunkt Wa. Zeigen sie, dass die Wendepunkte Wa auf einer parallelen zur t-Achse liegen

Die 2. Ableitung:

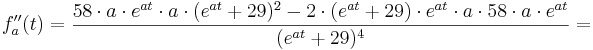
f''_{a}(t) = \frac{58\cdot a \cdot e^{at}\cdot a\cdot(e^{at}+29)^{2} - 2 \cdot(e^{at} + 29)\cdot e^{at}\cdot a \cdot 58 \cdot a \cdot e^{at} }{(e^{at} + 29) ^{4} } =
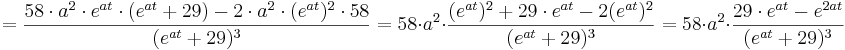
= \frac{58\cdot a^{2} \cdot e^{at}\cdot (e^{at} + 29) - 2\cdot a^{2} \cdot (e^{at})^{2}\cdot 58 }{(e^{at}+29)^{3}} = 58\cdot a^{2}\cdot \frac{(e^{at})^{2} + 29\cdot e^{at} - 2(e^{at})^2}{(e^{at} + 29)^{3}} = 58\cdot a^{2} \cdot \frac {29\cdot e^{at} - e^{2at}}{(e^{at}+29)^{3}}

Suche nach dem Wendepunkt:

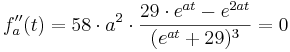
f''_{a}(t) = 58\cdot a^{2} \cdot \frac {29\cdot e^{at} - e^{2at}}{(e^{at}+29)^{3}} = 0 

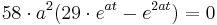
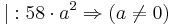
58\cdot a^{2} (29\cdot e^{at} - e^{2at}) = 0                              | : 58\cdot a^{2} \Rightarrow (a \neq 0)
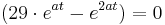
       (29\cdot e^{at} - e^{2at}) = 0                              | + e^{2at}\;  
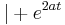
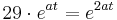
               29 \cdot e^{at} = e^{2at}                            | ln\;
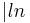
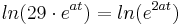
           ln(29\cdot e^{at}) = ln(e^{2at})
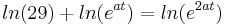
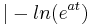
      ln(29) + ln(e^{at}) = ln(e^{2at})\;                       | - ln(e^{at})\;
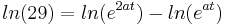
                ln(29) = ln(e^{2at}) - ln(e^{at})\;
                ln(29) = 2\cdot a\cdot t \cdot ln(e) - a\cdot t\cdot ln(e)    (ln(e)=1)
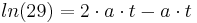
                ln(29) = 2\cdot a\cdot t - a\cdot t
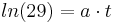
                ln(29) = a\cdot t
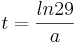
                      t = \frac {ln29} {a}

Beweis für Wendepunkt:

1. Möglichkeit: Die H-Methode

Man nähert sich dem möglichen Wendepunkt mit Hilfe eines Grenzwertes an und versucht herauszufinden, ob ein Vorzeichenwechsel am Wendepunkt stattfindet. Falls es einen Vorzeichenwechsel geben sollte, ist dies der eindeutige Beweis für einen Wendepunkt an dieser Stelle. 

f''_{a}(t+h) = \lim_{h \to 0} 58\cdot a^{2}\cdot \frac {29\cdot e^{a\cdot(t+h)} - e^{2a\cdot(t+h)}}{(e^{a\cdot (t+h)}+29)^{3}} = 58\cdot 29\cdot a^{2}\lim_{h \to 0} \frac {e^{(at + ah)} - e^{(2at + 2ah)}}{(e^{(at + ah)} + 29)^{3}} =

2. Möglichkeit:

3. Möglichkeit:

Zeichnen sie die Graphen G0,75 und G1 in ein und dasselbe Koordinatensystem und schlussfolgern Sie, welchen Einfluss der Parameter a auf den Verlauf der Graphen Ga hat

Der Graph

Graph-facharbeit1.png

Von „http://rmg.zum.de/index.php?title=Facharbeit_Mathematik_Straßheimer/Die_Aufgabe/Lösung_b)&oldid=26914“