Lineare Ungleichungen: Unterschied zwischen den Versionen
K (→Lösungsmenge) |
|||
| Zeile 48: | Zeile 48: | ||
'''<span style="color: darkorange">></span>''' & '''<span style="color: darkorange"><</span>''' - Zeichen <span style="color: darkorange">schließen eine Zahl aus</span>!<br /> | '''<span style="color: darkorange">></span>''' & '''<span style="color: darkorange"><</span>''' - Zeichen <span style="color: darkorange">schließen eine Zahl aus</span>!<br /> | ||
| − | <math>\ge</math> & <math>\le</math> - Zeichen <span style="color: darkorange">schließen die jeweilige Zahl mit ein</span>!<br /><br /><br /> | + | <math>{\color{red}\ge}</math> & <math>{\color{red}\le}</math> - Zeichen <span style="color: darkorange">schließen die jeweilige Zahl mit ein</span>!<br /><br /><br /> |
<span style="color: darkorange">'''Arbeitsauftrag 1:'''</span> Fasse die Lösungsmenge L <math>\lbrace</math>x | x <math>\le</math> 100<math>\rbrace</math> in Bezug auf die Tarife A & B in Worte! | <span style="color: darkorange">'''Arbeitsauftrag 1:'''</span> Fasse die Lösungsmenge L <math>\lbrace</math>x | x <math>\le</math> 100<math>\rbrace</math> in Bezug auf die Tarife A & B in Worte! | ||
Version vom 3. Januar 2010, 13:09 Uhr
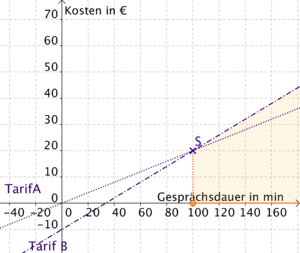
Im Prinzip haben wir es beim Unterpunkt "Schnittpunkt" des vorigen Kapitels mit einer Ungleichung zu tun gehabt. Da wir eine Grafik zur Veranschaulichung hatten, konnten wir die Fragestellung mithilfe des Schnittpunktes finden. Wollen/Können wir die Lösung nicht anhand einer Zeichnung festmachen, so muss man die Aufgabe mit einer Ungleichung lösen!
Inhaltsverzeichnis |
Lösen einer Ungleichung
Jonas: Ab welcher Minute ist Tarif B teurer als Tarif A?
 Wir fragen also: Für welche x-Werte ist Tarif B größer als Tarif A?
Wir fragen also: Für welche x-Werte ist Tarif B größer als Tarif A?
Tarif A: f (x) = 0,2x
Tarif B: f (x) = 0,3x - 10
Auswählen eines Ungleichheitszeichens: > "größer als" < "kleiner als" 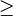 "größer gleich"
"größer gleich"  "kleiner gleich"
"kleiner gleich"
Ungleichung aufstellen: Tarif B > Tarif A; 0,3x - 10 > 0,2 x
nach x auflösen: 0,1x > 10; x > 100
 Für alle x-Wert, die größer sind als 100, ist Tarif B größer als Tarif A. Also ist Tarif B ab der 101. Minute teurer!
Für alle x-Wert, die größer sind als 100, ist Tarif B größer als Tarif A. Also ist Tarif B ab der 101. Minute teurer!
Eine Ungleichung verbindet zwei Terme durch ein Ungleichheitszeichen: >, 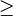 , <,
, <, 
Lösungsmenge & Intervall
Um die Lösung in mathematischer Schreibweise und nicht als ganzen Satz angeben zu können, gibt es hier zwei Möglichkeiten...
Lösungsmenge
L 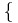 x | x > 100
x | x > 100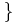 (lies: "Menge aller Zahlen, die größer sind als 100")
(lies: "Menge aller Zahlen, die größer sind als 100")
Der Zahlenstrahl veranschaulicht diese Menge...
Wegen des > - Zeichens gehört die Zahl 100 nicht mehr zur Menge und wird mit einem unausgefüllten Kreis dargestellt.
anderes Beispiel: L 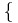 x | x
x | x  100
100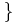 (lies: " Menge aller Zahlen, die kleiner oder gleich 100 sind")
(lies: " Menge aller Zahlen, die kleiner oder gleich 100 sind")
![]()
> & < - Zeichen schließen eine Zahl aus!
 &
&  - Zeichen schließen die jeweilige Zahl mit ein!
- Zeichen schließen die jeweilige Zahl mit ein!
Arbeitsauftrag 1: Fasse die Lösungsmenge L 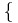 x | x
x | x  100
100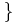 in Bezug auf die Tarife A & B in Worte!
in Bezug auf die Tarife A & B in Worte!
Die Lösungsmenge L 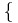 x | x < c
x | x < c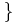 (L
(L 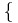 x | x > c
x | x > c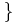 , L
, L 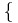 x | x
x | x 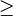 c
c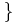 , L
, L 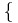 x | x
x | x  c
c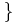 ):
):
Menge aller Zahlen , die größer (kleiner, größer gleich, kleiner gleich)
als eine Zahl c sind, an.
Intervallschreibweise
I =  100;
100;
 (lies: "Das Intervall von ausschließlich Hundert bis plus Unendlich")
(lies: "Das Intervall von ausschließlich Hundert bis plus Unendlich")
Die Richtungen der Klammern geben an, ob eine Zahl ein-oder ausgeschlossen ist...
Nach innen geöffnet schließt sie eine Zahl in das Intervall ein
Nach außen geöffnet schließt sie eine Zahl aus dem Intervall aus

 ("plus Unendlich) &
("plus Unendlich) & 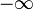 ("minus Unendlich") sind immer ausgeschlossen!
("minus Unendlich") sind immer ausgeschlossen!
Arbeitsauftrag 2: Gib die Lösungsmenge L 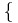 x | x
x | x  100
100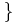 in Intervallschreibweise ohne
in Intervallschreibweise ohne  - oder
- oder 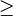 -Zeichen an!
-Zeichen an!
I =  a;b
a;b  ( I =
( I =  a;b
a;b  , I =
, I =  a;b
a;b  , I =
, I =  a;b
a;b  ):
):
Die Menge aller Zahlen von einschließlich a bis einschließlich b
(einschließlich...ausschließlich, ausschließlich...einschließlich, ausschließlich...einschließlich)
+
 & -
& - sind ausgeschlossen!
sind ausgeschlossen!
Umformunsregeln
Im Grunde gelten für gelten für Ungleichungen die gleichen Äquvivalenzumformungen wie bei linearen Gleichungen bis auf eine Ausnahme...
- Auf beiden Seiten eine gleiche Zahl (Term) addieren oder subtrahieren...
2x - 4 > 8 + x | + 4
2x - 4 + 4 > 8 + 4 + x
2x > 12 + x | - x
2x - x > 12 + x - x
x > 12
- Beide Seiten mit einer gleichen positiven Zahl (Term) multiplizieren oder durch sie teilen...
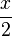 < 8 | * 2
< 8 | * 2
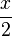 * 2 < 8 * 2
* 2 < 8 * 2
x < 16
- Beide Seiten mit der gleichen negativen Zahl (Term) multiplizieren oder durch sie teilen und das Ungleichheitszeichen umdrehen...
-4x < 6 | : (-4)
-4x : (-4) > 6 : (-4)
x > 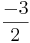
Beim Multiplizieren & Dividieren einer negativen Zahl wir das Ungleichheitszeichen umgedreht!