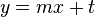Die lineare Funktion: Unterschied zwischen den Versionen
(→Geradengleichung) |
(→Geradengleichung) |
||
| Zeile 44: | Zeile 44: | ||
m = <math>\frac{2}{4}</math> = <math>\frac{1}{2}</math> <br /><br /> | m = <math>\frac{2}{4}</math> = <math>\frac{1}{2}</math> <br /><br /> | ||
Die Steigung m dieser Geraden beträgt also <u>an jeder Stelle</u> 0,5!<br /><br /> | Die Steigung m dieser Geraden beträgt also <u>an jeder Stelle</u> 0,5!<br /><br /> | ||
| − | ''' | + | |
| − | + | <span style="color: darkorange">'''Arbeitsauftrag 1'''</span>: Verändere im GeoGebra-Applet am Schieberegler m ein paar mal die Steigung und versuche Aussagen über den Zusammenhang zwischen Steigung m und dem Aussehen des Graphen der Geraden zu machen! | |
| − | <span style="color: darkorange">'''Arbeitsauftrag'''</span>: Versuche die Steigung unseres "Ufo-Beispiels" zu bestimmen!<br /> | + | (Wie verhält sich der Graph bei kleinerem bzw. größerem Betrag von m? Was kann man bei positivem bzw. negativem m beobachten?)<br /> |
| + | <span style="color: darkorange">'''Arbeitsauftrag 2'''</span>: Versuche die Steigung unseres "Ufo-Beispiels" zu bestimmen! Zeichne dazu ein geeignetes Steigungsdreieck in die Grafik auf deinem Arbeitsblatt ein!<br /> | ||
| + | |||
{| class="prettytable" | {| class="prettytable" | ||
|- | |- | ||
| 1 |'''Steigung m: m = <math>\frac{\partial x}{\partial y}</math> = Höhenzuwachs / waagrechten Zuwachs'''<br /> | | 1 |'''Steigung m: m = <math>\frac{\partial x}{\partial y}</math> = Höhenzuwachs / waagrechten Zuwachs'''<br /> | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| Zeile 68: | Zeile 69: | ||
'''Ist t negativ, wird die Gerade nach unten verschoben.'''<br /> | '''Ist t negativ, wird die Gerade nach unten verschoben.'''<br /> | ||
| − | <span style="color: darkorange">'''Arbeitsauftrag'''</span>: Bestimme wieder den y-Abschnitt des "Ufo-Beispiels"!<br /> | + | <span style="color: darkorange">'''Arbeitsauftrag 1'''</span>: Zeichne auf deinem Arbeitsbaltt eine Gerade mit der Steigung m = 2 und dem y-Abschnitt t = 1 in das Koordinatensystem!<br /> |
| − | + | <span style="color: darkorange">'''Arbeitsauftrag 2'''</span>: Bestimme wieder den y-Abschnitt des "Ufo-Beispiels"!<br /> | |
{| class="prettytable" | {| class="prettytable" | ||
|- | |- | ||
| Zeile 78: | Zeile 79: | ||
=== <span style="color: blue">Zusammenfassung</span> === | === <span style="color: blue">Zusammenfassung</span> === | ||
| − | Eine Funktion der Form <math>f(x) = mx + t</math> heißt lineare Funktion. Der Graph einer linearen Funktion ist eine Gerade.<br /><br /> | + | Eine Funktion der Form <math>f(x) = mx + t</math> heißt '''lineare Funktion'''. Der Graph einer linearen Funktion ist eine '''Gerade'''.<br /><br /> |
| − | Eine Gerade hat die Steigung m und den y-Abschnitt t. <br /> | + | Eine Gerade hat die Steigung m und den y-Abschnitt t. <br /><br /> |
| + | |||
| + | '''m = <math>\frac{\partial x}{\partial y}</math>'''<br /> | ||
| + | '''m > 0''' → Gerade steigt<br /> | ||
| + | '''m < 0''' → Gerade fällt<br /> | ||
| + | Je größer '''|m|''' umso steiler die Gerade!<br /><br /> | ||
| + | |||
| + | '''t > 0''' → die Gerade schneidet die y-Achse oberhalb des Ursprungs<br /> | ||
| + | '''t < 0''' → die Gerade schneidet die y-Achse unterhalb des Ursprungs<br /><br /> | ||
| + | |||
<span style="color: blue">'''m'''</span> und <span style="color: blue">'''t'''</span> sind feste Zahlen, <span style="color: blue">'''Parameter'''</span>, die die Gerade eindeutig festlegen.<br /> | <span style="color: blue">'''m'''</span> und <span style="color: blue">'''t'''</span> sind feste Zahlen, <span style="color: blue">'''Parameter'''</span>, die die Gerade eindeutig festlegen.<br /> | ||
Im Gegensatz dazu sind <span style="color: darkorange">'''x'''</span> und <span style="color: darkorange">'''y'''</span> unbekannte Größen, <span style="color: darkorange">'''Variablen'''</span>. | Im Gegensatz dazu sind <span style="color: darkorange">'''x'''</span> und <span style="color: darkorange">'''y'''</span> unbekannte Größen, <span style="color: darkorange">'''Variablen'''</span>. | ||
| − | Zusammen bilden sie die Geradengleichung <br /> | + | Zusammen bilden sie die '''Geradengleichung''' <br /> |
| − | <math>y = m x + t</math> | + | '''<math>y = m x + t</math>''' |
== <span style="color: darkblue">Besondere Geraden</span>== | == <span style="color: darkblue">Besondere Geraden</span>== | ||
== <span style="color: darkblue">Aufgaben</span>== | == <span style="color: darkblue">Aufgaben</span>== | ||
Version vom 11. Oktober 2009, 11:56 Uhr
Inhaltsverzeichnis |
Geradengleichung
Ufos versenken
Zuerst einmal die wichtigste Grundlage, um mit linearen Funktionen umgehen zu können - die Geradengleichung.
Sie legt eine solche Funktion eindeutig fest.
Zum Einstieg ein kleines Spiel!
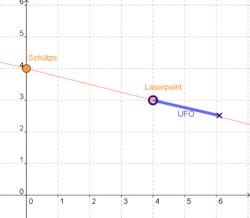
Beim Ufos versenken geht es darum dem Schützen so genau wie möglich die Daten für die Schusslinie mitzuteilen, damit dieser dann erfolgreich die feindlichen Ufos abwehren kann.
Er muss zum einen wissen von welcher Position aus er schießen muss und zum andern welche Richtung er anpeilen muss.
Peile mit dem Laserpoint (rotes Kreuz) jeweils den Bug (blauer Kreis) des Ufos an und richte dann die Schusslinie so aus, dass sie auch das Heck (blaues Kreuz) genau durchläuft. Hierzu kannst du sowohl Schütze als auch Laserpoint mit der Maus verschieben.
Trage die Koordinaten anschließend auf deinem Arbeitsblatt ein und vergleiche zum Schluss deine Ergebnisse!
Hier ein Beispiel:
| Schütze | Laserpoint |
| 4 | -1 / 4 |
Die Lage des Laserpoints gibts du mit den Koordinaten vom Schützen ausgehend an!
Das Steigungsdreieck
Du hast dem Schützen nun zwei wichtige Informationen mitgeteilt, mit deren Hilfe sich die Schusslinie - eine Gerade - aufstellen lässt.
Zuerst einmal die Steigung - Sie wird in der Mathematik mit m bezeichnet!
Indem du vom Schützen ausgehend die Lage des Laserpoints ermittelt hast, hast du nicht anderes getan, als ein sogenanntes Steigunsdreieck zu beschreiben.
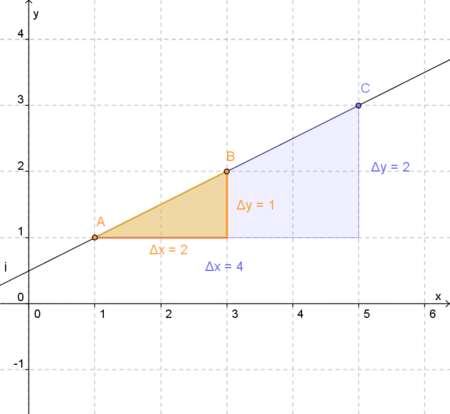
Im Beispiel gehen wir vom Punkt A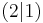 
aus um 2 Einheiten nach rechts,
um eine Einheit nach oben und kommen so bei Punkt B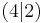 
wieder an. Daraus entsteht das rechtwinklige Steigungsdreieck, dessen Katheten einmal
den waagrechten Zuwachs,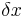 
, und den Höhenzuwachs, 
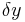, anzeigen.
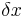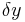und ist jeweils die Differenz aus den beiden x- bzw. y-Werten der Punkte A und B.
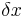→ = xB - xA = 4 - 2 = 2
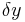→ = yB - yA = 2 - 1 = 1
Der Quotient "Höhenzuwachs durch waagrechten Zuwachs" ergibt die Steigung m.
m =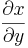 
= 
Dabei ist es völlig egal bei welchem Punkt man startet bzw. wie groß das Steigungsdreieck ist,
da das Verhältnis der beiden Katheten immer das gleiche bleibt.
Nehmen wir zum Beipiel das zweite Steigungsdreieck:
m = 
=
Die Steigung m dieser Geraden beträgt also an jeder Stelle 0,5!
Arbeitsauftrag 1: Verändere im GeoGebra-Applet am Schieberegler m ein paar mal die Steigung und versuche Aussagen über den Zusammenhang zwischen Steigung m und dem Aussehen des Graphen der Geraden zu machen!
(Wie verhält sich der Graph bei kleinerem bzw. größerem Betrag von m? Was kann man bei positivem bzw. negativem m beobachten?)
Arbeitsauftrag 2: Versuche die Steigung unseres "Ufo-Beispiels" zu bestimmen! Zeichne dazu ein geeignetes Steigungsdreieck in die Grafik auf deinem Arbeitsblatt ein!
| Steigung m: m = 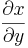= Höhenzuwachs / waagrechten Zuwachs |
Der y-Abschnitt
Die zweite wichtige Information hast du gewissermaßen mit der Lage des Schützen angegeben.
Jede Gerade schneidet in einem bestimmten Punkt die y-Achse! Das kann sowohl im positiven als auch im negativen Bereich passieren.
Diesen Schnittpunkt mit der y-Achse nennt man y-Abschnitt - er wird gewöhnlich mit t bezeichnet.
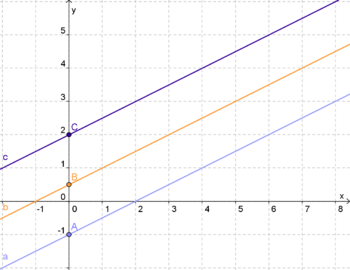
Im Beipiel siehst du drei verschiedene Geraden, mit dem y-Abschnitt
tA = -1
tB = 0.5
tC = 3
Ein positives t verschiebt also die Gerade ein Stück nach oben (vom Ursprung ausgehend), lässt sie im positiven Bereich mit der y-Achse schneiden.
Ist t negativ, wird die Gerade nach unten verschoben.
Arbeitsauftrag 1: Zeichne auf deinem Arbeitsbaltt eine Gerade mit der Steigung m = 2 und dem y-Abschnitt t = 1 in das Koordinatensystem!
Arbeitsauftrag 2: Bestimme wieder den y-Abschnitt des "Ufo-Beispiels"!
| y-Abschnitt t: Schnittpunkt der Geraden mit der y-Achse |
Zusammenfassung
Eine Funktion der Form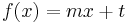 
heißt lineare Funktion. Der Graph einer linearen Funktion ist eine Gerade.
Eine Gerade hat die Steigung m und den y-Abschnitt t.
m =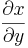
m > 0 → Gerade steigt
m < 0 → Gerade fällt
Je größer |m| umso steiler die Gerade!
t > 0 → die Gerade schneidet die y-Achse oberhalb des Ursprungs
t < 0 → die Gerade schneidet die y-Achse unterhalb des Ursprungs
m und t sind feste Zahlen, Parameter, die die Gerade eindeutig festlegen.
Im Gegensatz dazu sind x und y unbekannte Größen, Variablen.
Zusammen bilden sie die Geradengleichung
