Übungen1: Unterschied zwischen den Versionen
(→Übung 3: +aufgabe) |
|||
| Zeile 47: | Zeile 47: | ||
<big>f(x) = - 2x<sup>2</sup></big> (Die Parabel ist nach unten geöffnet.) (!Die Parabel ist nach oben geöffnet.) (Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (!Der Punkt [0|-2] liegt auf dem Graphen.) (Der Punkt [1|2] liegt oberhalb des Graphen.) | <big>f(x) = - 2x<sup>2</sup></big> (Die Parabel ist nach unten geöffnet.) (!Die Parabel ist nach oben geöffnet.) (Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (!Der Punkt [0|-2] liegt auf dem Graphen.) (Der Punkt [1|2] liegt oberhalb des Graphen.) | ||
| + | |||
| + | <big>f(x) = 0,2x<sup>2</sup></big> (!Die Parabel ist nach unten geöffnet.) (Die Parabel ist nach oben geöffnet.) (!Die Parabel ist enger als die Normalparabel.) (Die Parabel ist weiter als die Normalparabel.) (!Der Punkt [-1|2] liegt auf dem Graphen.) (Der Punkt [-1|1] liegt oberhalb des Graphen.) | ||
</div> | </div> | ||
Version vom 15. Februar 2009, 23:50 Uhr
Quadratische Funktionen/Übungen1 - Quadratische Funktionen/Übungen2 - Quadratische Funktionen/Abschlustest - Quadratische Funktionen/Übungen3
Übung 1
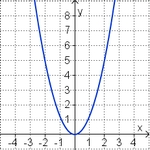
Die Graph der Funktion f mit f(x)=ax² heißt Parabel . Ist a = 1, so heißt der Graph Normalparabel.
Quadratische Funktionen liegen symmetrisch zur x-Achse.
Der Punkt S (0;0) heißt Scheitel .
Für a>0 gilt: Je größer a ist, desto steiler ist die Parabel.
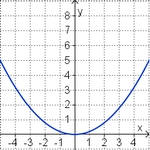
Für a>0 gilt: Je kleiner a ist, desto weiter ist die Parabel.
Übung 2
Ordne den Funktionsgraphen den richtigen Term zu
 |
 |
 |
 |
 |
|
| 0,5x2 | 2x2 | 3x2 | 0,75x2 | 1,25x2 | 0,2x2 |
Übung 3
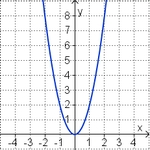
f(x) = 3,5x2 (!Die Parabel ist nach unten geöffnet.) (Die Parabel ist nach oben geöffnet.) (Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (Der Punkt [2|14] liegt auf dem Graphen.) (Der Punkt [14|2] liegt nicht auf dem Graphen.)
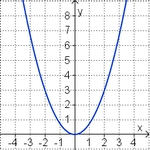
f(x) = - 0,5x2 (Die Parabel ist nach unten geöffnet.) (!Die Parabel ist nach oben geöffnet.) (!Die Parabel ist enger als die Normalparabel.) (Die Parabel ist weiter als die Normalparabel.) (Der Punkt [2|-2] liegt auf dem Graphen.) (!Der Punkt [2|2] liegt auf dem Graphen.)
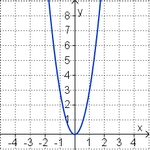
f(x) = - 2x2 (Die Parabel ist nach unten geöffnet.) (!Die Parabel ist nach oben geöffnet.) (Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (!Der Punkt [0|-2] liegt auf dem Graphen.) (Der Punkt [1|2] liegt oberhalb des Graphen.)
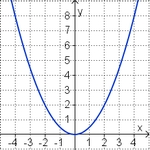
f(x) = 0,2x2 (!Die Parabel ist nach unten geöffnet.) (Die Parabel ist nach oben geöffnet.) (!Die Parabel ist enger als die Normalparabel.) (Die Parabel ist weiter als die Normalparabel.) (!Der Punkt [-1|2] liegt auf dem Graphen.) (Der Punkt [-1|1] liegt oberhalb des Graphen.)
