|
2) Nebenstehende Vierfeldertafel gehört zu einem zweistufigen Zufallsexperiment mit den zwei Ereignissen A und B.
a) Fülle die Vierfeldertafel vollständig aus.
b) Mit welcher Wahrscheinlichkeit tritt das Ereignis
i) B ein
ii) A 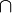 B ein B ein
iii) A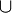 B ein B ein
iv) 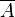 ein, wenn bekannt ist, dass B bereits eingetreten ist. ein, wenn bekannt ist, dass B bereits eingetreten ist.
|
|
 Knicktest - Mehrstufige Zufallsexperimente (Baumdiagramm, Vierfeldertafel, Bedingte Wahrscheinlichkeit) |