Lernpfad zur zentrischen Streckung und den Ähnlichkeitssätzen/Ähnlichkeit - Übung 4
Aufgabe 1
Aufgabe:
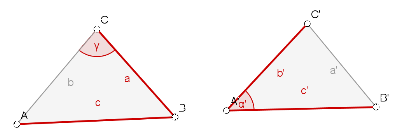
Stelle fest, ob die Dreiecke ABC und A'B'C' ähnlich sind, wenn:
a) a = 5; b = 8; c = 10 und a' = 2,5; b' = 4; c' = 5
b)  = 30°;
= 30°; 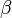 = 100° und
= 100° und 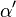 = 50°;
= 50°; 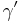 = 100°
= 100°
c) a = 5; c = 8; 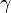 = 100° und b' = 2,5; c' = 4;
= 100° und b' = 2,5; c' = 4; 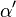 = 100°
= 100°
Tipp: Wenn du unsicher bist kann dir eine Skizze helfen, in der du die gegebenen Seiten bzw. Winkel farbig markierst!
a) Die beiden Dreiecke sind ähnlich, da sie im Verhältnis ihrer Seiten übereinstimmen (S : S : S - Satz).
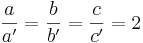
b) Die beiden Dreiecke sind ähnich, da sie in zwei Winkeln übereinstimmen (WW - Satz).
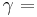 180° - (
180° - ( +
+ 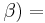 180° - (30° + 100°)
180° - (30° + 100°)  50°
50° 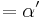
c) Die Dreiecke sind nicht ähnlich. Im Dreieck ABC sind zwei Seiten und ein Gegenwinkel, im Dreieck A'B'C' zwei Seiten und der Zwischenwinkel bekannt.
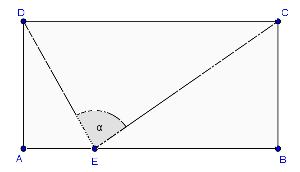
Aufgabe 2
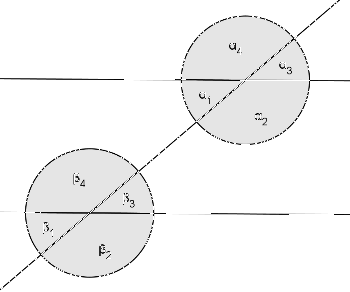
Zur Erinnerung hier noch einmal die verschiedenen Winkelarten.
- Nebenwinkel: ergänzen sich zu 180° z. B.
 1 und
1 und  2
2
- Scheitelwinkel: sind gleich groß z. B.
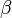 2 und
2 und 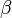 4
4
- Wechselwinkel: sind gleich groß z. B.
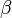 1 und
1 und  3
3
- Stufenwinkel: sind gleich groß z. B.
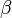 2 und
2 und  2
2
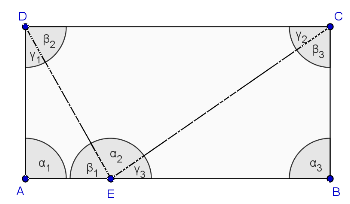
Dies ist nur ein Lösungsvorschlag, es gibt mehr als eine richtige Lösung!
 1
1 
 2
2 
 3
3  90° (gegeben oder wegen Rechteck)
90° (gegeben oder wegen Rechteck)
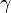 2
2 
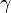 3 (Wechselwinkel)
3 (Wechselwinkel)
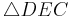 ~
~ 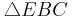 (WW - Satz)
(WW - Satz)
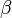 1
1 
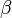 2 (Wechselwinkel)
2 (Wechselwinkel)
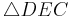 ~
~ 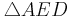 (WW - Satz)
(WW - Satz)
 Die drei Dreiecke sind zueinander ähnlich
Die drei Dreiecke sind zueinander ähnlich