Satz des Pythagoras - Seite 1
Der Satz des Pythagoras
|
Auf dem Bild links siehst du die Rügenbrücke in Stralsund. Sie ist ein Beispiel für eine Schrägseilbrücke. Eines der Stahlseile ist spröde und man will wissen wie lang ein neues Seil sein muss. Da sich jedoch niemand traut das Seil abzulaufen, kennt man seine Länge nicht. Bevor jedoch die Länge des Stahlseiles nicht bekannt ist, wird auch kein neues gekauft und so lange muss die Brücke gesperrt bleiben. Nun steht man vor der Frage: Wie kann man die Länge des Stahlseiles durch Rechnung ermitteln? |
Hole dir das Arbeitsblatt Zerlegungsbeweis zum Satz des Pythagoras!
Arbeitsauftrag:
- Zerschneide die Quadrate über den Katheten in dem oberen Dreieck auf dem Blatt an den eingezeichneten Linien
- Versuche die Teile auf das Quadrat über der Hypotenuse im unteren Dreieck zu verteilen
- Was fällt dir auf?
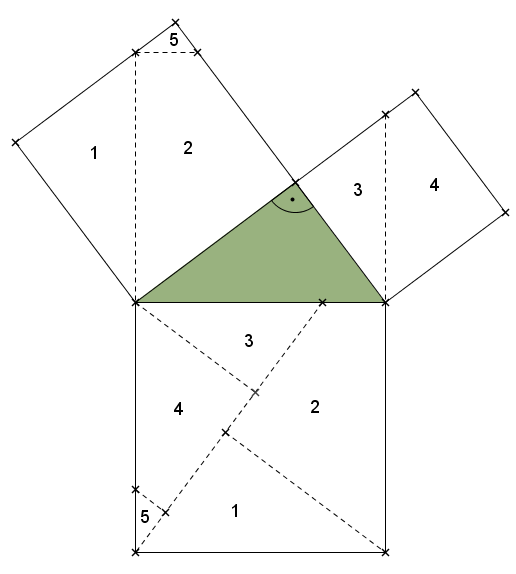
- Hier die Lösung, wie man die Quadrate verteilen kann:
- Die Quadrate über den Katheten lassen sich auf das Quadrat über der Hypotenuse verteilen.
- Der Satz des Pythagoras sagt also, dass in jedem beliebigen rechtwinkligen Dreieck gilt:
- Der Flächeninhalt des Quadrats über der Hypotenuse ist gleich der Summe der Flächeninhalte der Quadrate über den Katheten
- Hinweis: Ihr habt eben einen Beweis geführt, dass der Satz des Pythagoras in rechtwinkligen Dreiecken gilt. Diesen Beweis nennt man Zerlegungsbeweis.
Arbeitsauftrag:
- Klebe das untere Dreieck vom Arbeitsblatt zum Zerlegungsbeweis mit den aufgeteilten Kathetenquadraten unter der Überschrift "Der Satz des Pythagoras" in dein Heft ein
- Notiere dir das Ergebnis des Beweises unter dem Dreieck
Wenn du fertig bist geht es hier weiter.