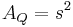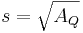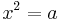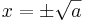Satz des Pythagoras - Seite 2
Aus RMG-Wiki
Der Satz des Pythagoras
|
Wir erinnern uns: |
|
Übertragen wir das auf den Satz des Pythagoras: 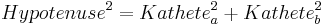
Das ist die Formel zu dem Ergebnis des Zerlegungsbeweises
In Worten: Das Quadrat über der Hpotenuse ist Flächengleich zur Summe der Quadrate über den beiden Katheten
- Kennen wir also beispielsweise die Länge der beiden Katheten (damit den Flächeninhalt ihrer Quadrate und aus der Summe der beiden Quadrate den Flächeninhalt der Hypotenuse) und möchten die Länge der Hypotenuse erfahren, rechnen wir:
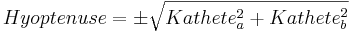
- Kennen wir die Länge einer Kathete und der Hypotenuse formen wir die Gleichung zunächst um:
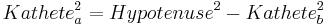
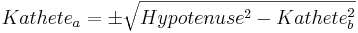
|
Wir erinnern uns: |
|
Arbeitsauftrag:
- Notiere dir den Satz des Pythagoras als Formel:
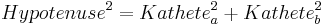
- Notiere ebenfalls die Folgerungen für die Länge der Hypotenuse und die einer Kathete
Wenn du fertig bist geht es hier zu ein paar Übungen