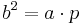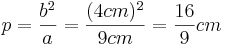Lösungen zum Übungsblatt zum Kathetensatz (Aufgaben 1-5)
Aus RMG-Wiki
< Lernpfad zur Satzgruppe des Pythagoras(Weitergeleitet von Lernpfad zur Satzgruppe des Pythagoras/Übungen zum Kathetensatz)
Arbeitsauftrag:
- Hole dir das Übungsblatt zum Kathetensatz
- Bearbeite die Aufgaben 1-5 und vergleiche deine Lösungen mit denen auf der Seite
Aufgabe 1
Aufgabe 2
Aufgabe 3
Aufgabe 4
Aufgabe 5
Wenn du fertig bist geht es hier zu einer Anwendung des Kathetensatzes
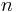 an
an 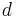 anliegt, muss
anliegt, muss 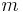 an
an 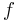 anliegen
anliegen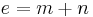
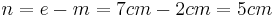
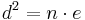
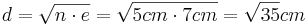
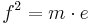
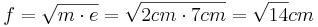
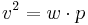
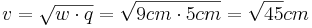
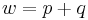
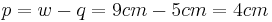
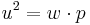
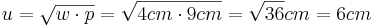
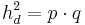
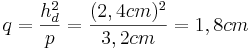
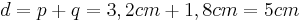
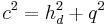 (Man berechnet c über den Satz des Pythagoras im kleinen rechtwinkligen Dreieck)
(Man berechnet c über den Satz des Pythagoras im kleinen rechtwinkligen Dreieck)
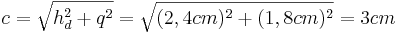
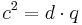 (Man berechnet c über den Kathetensatz im ganzen rechtwinkligen Dreieck)
(Man berechnet c über den Kathetensatz im ganzen rechtwinkligen Dreieck)
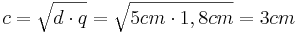
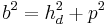 (Man berechnet b über den Satz des Pythagoras im kleinen rechtwinkligen Dreieck)
(Man berechnet b über den Satz des Pythagoras im kleinen rechtwinkligen Dreieck)
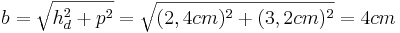
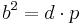 (Man berechnet c über den Kathetensatz im ganzen rechtwinkligen Dreieck)
(Man berechnet c über den Kathetensatz im ganzen rechtwinkligen Dreieck)
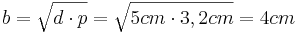
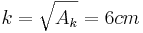
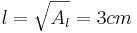
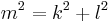
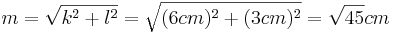
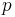 und
und 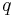 , wobei
, wobei 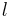 anliegt
anliegt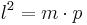
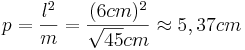
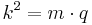
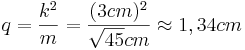
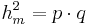
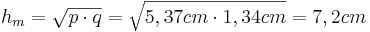
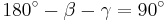
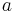 ist Hypotenuse, da
ist Hypotenuse, da 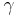 bei
bei 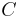 liegt und
liegt und 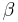 bei
bei 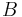 , d.h. dem Winkel
, d.h. dem Winkel 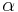 liegt die längste Seite, also
liegt die längste Seite, also 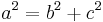
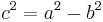
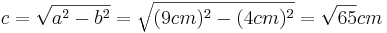
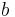 und
und