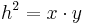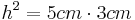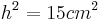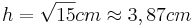Lösung zum Übungsblatt zum Höhensatz (Aufgabe 7)
Aus RMG-Wiki
< Lernpfad zur Satzgruppe des Pythagoras(Weitergeleitet von Lernpfad zur Satzgruppe des Pythagoras/Übung Umwandlung Rechteck in flächengleiches Quadrat)
Arbeitsauftrag:
- Löse Aufgabe 7 vom Übungsblatt zum Höhensatz in deinem Heft
- Vergleiche deine Lösung mit der Lösung auf der Seite
- Bearbeite die Zusatzaufgabe auf der Seite und vergleiche deine Lösung
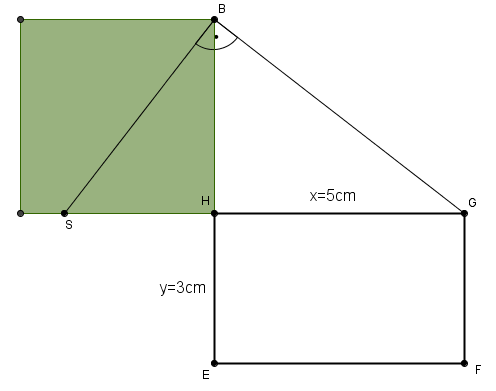
Aufgabe 7
![{[HB]\,}](/images/math/e/e/5/ee51f811add85303ddb0a901491771c4.png) ist die Höhe des rechtwinkligen Dreiecks
ist die Höhe des rechtwinkligen Dreiecks 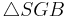
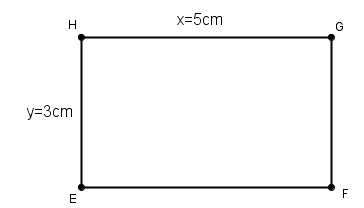
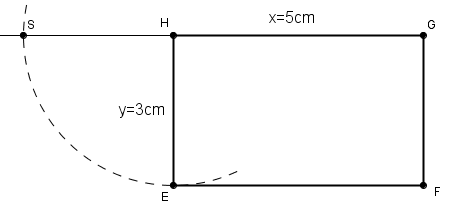
- Das Quadrat über
![{[HB]\,}](/images/math/e/e/5/ee51f811add85303ddb0a901491771c4.png) antragen
antragen
- Das Quadrat über
![{[HB]\,}](/images/math/e/e/5/ee51f811add85303ddb0a901491771c4.png) ist flächengleich zum gegebenen Rechteck, da der Höhensatz gilt
ist flächengleich zum gegebenen Rechteck, da der Höhensatz gilt
Zusatzaufgabe
Berechne die exakte Seitenlänge des Quadrats und vergleiche sie mit der Länge des von dir konstruierten Quadrates!
- x und y sind die Hypotenusenabschnitte eines rechtwinkligen Dreieck
- Das Rechteck der Hypotenusenabschnitte ist gleich dem Quadrat über der Höhe
- Wenn du die Konstruktion richtig hast, sollte die Seitenlänge deines Quadrates etwa 3,87cm betragen
Hinweis:
- Wenn du dir einmal nicht sicher bist, ob deine Konstruktion richtig ist, kannst du über den Höhensatz die exakte Seitenlänge des Quadrates ausrechnen
- Wenn das von dir konstruierte Quadrat die gleiche Seitenlänge hat, hast du alles richtig gemacht
- Es können natürlich auch kleinere Abweichungen durch die Konstruktion entstehen
Wenn du fertig gerechnet hast geht es hier zum dritten und letzten Satz der Satzgruppe des Pythagoras
![{[GH]\,}](/images/math/e/6/f/e6f47aa0385a574dad732502ef79a357.png)
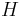 mit dem Radius
mit dem Radius ![{[HE]=y=3cm\,}](/images/math/2/7/1/2719ac04c919636491159fe0325067ad.png)
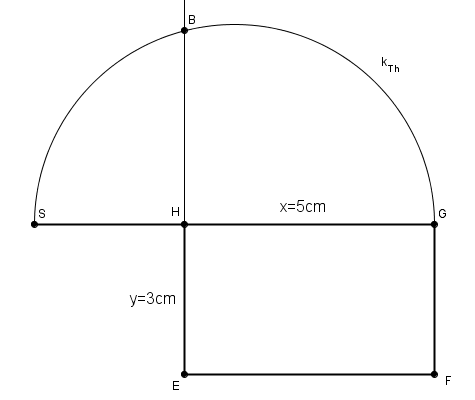
![{[SG]\,}](/images/math/b/6/f/b6faac04e7434cbb2d5b05b8e397ec7d.png)
![{[EH]\,}](/images/math/5/f/1/5f17a9cbf218452bcba37a77907607aa.png)