|
In einem kartesischen Koordinatensystem desIR3 sind die Punkte A(0|0|2), C(1|4|1) und D(-1|2|0) und die Gerade
g : 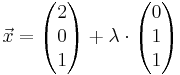 , λ ∈ IR, gegeben , λ ∈ IR, gegeben
1 a) Zeigen Sie, dass die drei Punkte A, C und D eine Ebene E festlegen, und bestimmen Sie eine Gleichung von E in Normalenform. [mögliches Ergebnis: F: 2x1-x2-23+4=0]
- [Lösung anzeigen][Lösung ausblenden]
1 b) Die Gerade g schneidet die Ebene E in einem Punkt B. Berechnen Sie die Koordinaten von B und zeigen Sie, dass der Punkt B das Dreieck ACD zu einem Quadrat ABCD ergänzt. [Teilergebnis: B(2|2|3)]
- [Lösung anzeigen][Lösung ausblenden]
2) Zusätzlich ist die Geradenschar ht : 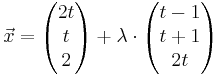 , λ.t ∈ IR gegeben. , λ.t ∈ IR gegeben.
2 a) Zeigen Sie, dass die Gerade g in der Schar der Geraden ht enthalten ist.
- [Lösung anzeigen][Lösung ausblenden]
2 b) Eine der Schargeraden ht ist parallel zur Ebene E. Bestimmen Sie den zugehörigen Scharparameter t und den Abstand dieser Geraden von E.
- [Lösung anzeigen][Lösung ausblenden]
3 a) Bestimmen Sie die Koordinaten des von B verschiedenen Punktes P ∈ g so, dass die Geraden PA und PC senkrecht zueinander stehen.
- [Lösung anzeigen][Lösung ausblenden]
3 b) Begründen Sie, dass es eine Kugel K mit Mittelpunkt M ∈ E gibt, auf der die Punkte A, B, C, D und P liegen. Ermitteln Sie die Koordinaten von M und den Radius r von K.
[zur Kontrolle: M(0,5 | 2 |1,5); r= 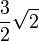
- [Lösung anzeigen][Lösung ausblenden]
3 c) Prüfen Sie, ob der Ursprung O des Koordinatensystems innerhalb oder außerhalb der Kugel K liegt, und geben Sie die Radien der Kugeln um den Ursprung an, die die Kugel K berühren.
- [Lösung anzeigen][Lösung ausblenden]
4) Für einen Punkt Q ∈ g wird der Flächeninhalt des Dreiecks AQC minimal. Bestimmen Sie diesen minimalen Flächeninhalt.
- [Lösung anzeigen][Lösung ausblenden]
|