- Aufgabe 1
Eine große Kiste enthält gut gemischt mehrere hundert rote, blaue, grüne
und gelbe Bausteine, die sich nur in ihrer Farbe unterscheiden. Jeder
fünfte Baustein ist gelb, 8 % sind grün. Außerdem befinden sich dreimal
so viele blaue wie grüne Steine in der Kiste.
a) Aus der Kiste werden 10 Bausteine zufällig entnommen. Zeigen Sie,
dass sich die Wahrscheinlichkeiten für das Ereignis „Keiner der
Bausteine ist grün“ bei den Modellen „Ziehen mit Zurücklegen“ und
„Ziehen ohne Zurücklegen“ um weniger als 0,2 Prozentpunkte
unterscheiden, wenn von einer Kiste mit 1000 Steinen ausgegangen
wird. (5 BE)
- [Lösung anzeigen][Lösung ausblenden]
Zuerst müssen die Wahrscheinlichkeiten für die 4 Farben berechnet werden:
Da jeder 5. Stein gelb ist, finden sich unter 100 Steinen 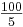 = 20 gelbe Steine. = 20 gelbe Steine.
Daraus folgt, dass die Wahrscheinlichkeit für einen gelben Stein P("gelb") = 0,2 ist.
Die Wahrscheinlichkeit für einen grünen Stein ist P("grün") = 0,08.
Aus es gibt dreimal so viele blaue wie grüne Steine in der Kiste folgt P("blau")= 3  0,08 = 0,24. 0,08 = 0,24.
Die restlichen Steine sind rot also ergibt sich für P("rot")= 1 - 0,2 - 0,08 - 0,24 = 0,48.
Unter 1000 Steinen befinden sich 0,08  1000 = 80 grüne Steine. 1000 = 80 grüne Steine.
Die Wahrscheinlichkeit, dass sich beim Ziehen von 10 Steinen unter den gezogenen kein grüner befindet, beträgt (Ziehen mit Zurücklegen):
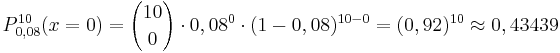
Die Wahrscheinlichkeit, dass sich beim Ziehen von 10 Steinen unter den gezogenen kein grüner befindet, beträgt (Ziehen ohne Zurücklegen):
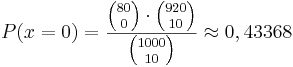
oder 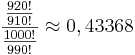
Antwort: Die Differenz ist mit: 0,43439 - 0,43268 = 0,00171 < 0,2 % vernachlässigbar.
Im Folgenden soll jeweils das Modell „Ziehen mit Zurücklegen“
verwendet werden.
b) Wie viele Bausteine müssen mindestens aus der Kiste zufällig entnommen
werden, damit mit einer Wahrscheinlichkeit von mehr als
75 % wenigstens ein grüner Baustein darunter ist? (4 BE)
- [Lösung anzeigen][Lösung ausblenden]
c) Lars denkt sich ein Spiel aus. Ein Spieler soll dazu 16 Bausteine aus
der Kiste zufällig entnehmen; für jeden gelben und für jeden blauen
Stein zahlt Lars 1 €, für jeden grünen 5 € an den Spieler. Für jeden
roten Baustein muss der Spieler jedoch einen bestimmten Betrag an
ihn zahlen. Wie hoch muss Lars diesen Betrag mindestens festsetzen,
damit er bei häufigem Spielen im Mittel keinen Verlust zu befürchten
hat? (5 BE)
- [Lösung anzeigen][Lösung ausblenden]
| X = k |
m |
1 |
5 |
| P(X = k) |
0,48 |
0,2 + 0,24 = 0,44 |
0,08 |
Lars hat nur dann im Mittel keinen Verlust, wenn der Erwartungswert für die Auszahlung gleich 0 ist.
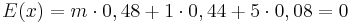 ; ;
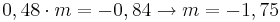 ; ;
Antwort: Für jeden roten Stein muss er mindestens 1,75€ verlangen.
Es werden zufällig 16 Bausteine aus der Kiste entnommen. Die beiden
Säulendiagramme zeigen die Wahrscheinlichkeiten, dabei k gelbe Steine
zu erhalten. Das linke Diagramm zeigt die zugehörige Binomialverteilung,
das rechte ergibt sich bei Näherung durch die Normalverteilung.
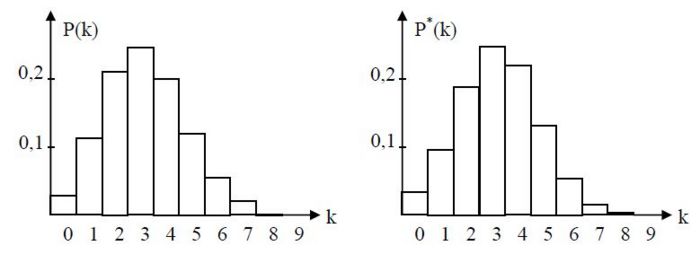
d) Prüfen Sie, ob das Kriterium für eine brauchbare Approximation der
Binomialverteilung durch die Normalverteilung erfüllt ist (vgl.
Formelsammlung). Zeigen Sie rechnerisch, dass es einen Wert für k
gibt, bei dem die in den Diagrammen dargestellten Wahrscheinlichkeiten
P(k) und P*(k) um mehr als 2 Prozentpunkte voneinander
abweichen. (7 BE)
- [Lösung anzeigen][Lösung ausblenden]
Die Bedingung der Brauchbarkeit findet sich in der Mathematikformelsammlung auf Seite 111 und lautet: n  p p  (1 - p) > 9; (1 - p) > 9;
Durch das Einsetzen von n = 16 (Es befinden sich 16 Steine in der Kiste) und p (Die Wahrscheinlichkeit für einen gelben Stein ist 0,2) erhält man:
16  0,2 0,2  0,8 = 2,56;
Da 2,56 < 9 ist, ist dieses Kriterium nicht erfüllt. 0,8 = 2,56;
Da 2,56 < 9 ist, ist dieses Kriterium nicht erfüllt.
Nun soll gezeigt werden, dass es einen Wert für k gibt, bei dem die in den Diagrammen dargestellten Wahrscheinlichkeiten P(k) und P*(k) um mehr als 2 Prozentpunkte voneinander abweichen.
Man sieht, dass die Werte für k = 1, k = 2 und k = 4 am deutlichsten voneinander abweichen. Außerdem wird deutlich, dass für k = 2 die beiden Werte am deutlichsten abweichen. Dies soll rechnerisch nachgeprüft werden:
Zuerst müssen für die Normalverteilung folgende Werte berechnet werden:
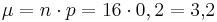
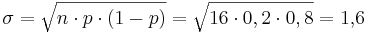
Also folgt:
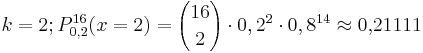
Approximation der Binomialverteilung durch die Normalverteilung (FS S.111):
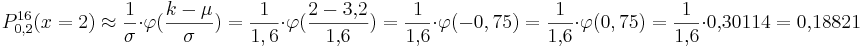
Anmerkung: aus Symetriegründen gilt: 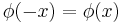
Die Werte für 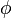 stammen aus dem Tafelwerk. stammen aus dem Tafelwerk.
Für die Differenz folgt: P(2) – P*(2) = 0,21111 - 0,09622 = 0,02290 > 0,02.
Antwort: Für k = 2 unterscheiden sich die beiden Werte um mehr als 2 %.
e) In die Kiste werden weitere gelbe Bausteine gegeben. Um wie viel
Prozent muss dabei die Anzahl der gelben Bausteine erhöht werden,
damit anschließend jeder dritte Baustein in der Kiste gelb ist? (3 BE)
- [Lösung anzeigen][Lösung ausblenden]
n ist die aktuelle Anzahl der Steine in der Kiste.
N ist die Anzahl der Steine in der Kiste, nach dem Hinzufügen von x Steinen.
k ist die aktuelle Anzahl der gelben Steine in der Kiste.
K ist die Anzahl der gelben Steine, nach dem Hinzufügen von x Steinen.
Damit jeder 3. Stein gelb ist, muss das Verhältnis "Alle gelben Steine " zu "Alle Steine in der Kiste " dem Verältnis "1" zu "3" entsprechen.
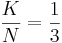 ; ;
Wenn x Steine hinzugefügt werden, ändert sich sowohl k als auch n.
K = k + x; und N = n + x;
Da aktuell jeder 5. Stein gelb ist, beträgt die Anzahl der gelben Steine in der Kiste 0,2  n. n.
Aus diesen Informatinen ergibt sich die Gleichung:
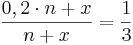 ; ;
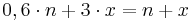 ; ;
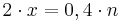 ; ;
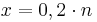 ; ;
Antwort: Weil x k entspricht, muss man genausoviele gelbe Steine, wie bereits vorhanden waren, hinzufügen, was einer Erhöhung um 100 % entspricht.
| 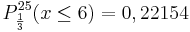
 20 = 480 verschieden Farbmuster für die "Treppe", wenn in jeder waagrechten Reihe ein blauer Stein sitzt.
20 = 480 verschieden Farbmuster für die "Treppe", wenn in jeder waagrechten Reihe ein blauer Stein sitzt.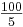 = 20 gelbe Steine.
= 20 gelbe Steine.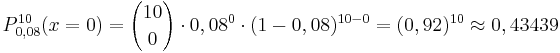
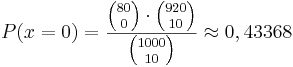
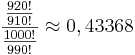
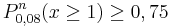
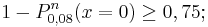
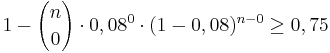 ;
;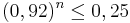 ;
;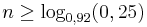 ;
;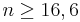 ;
;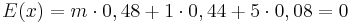 ;
;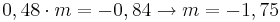 ;
;
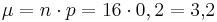
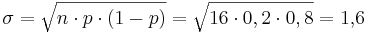
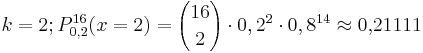
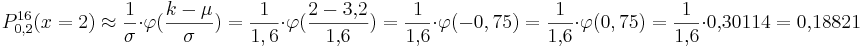
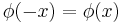
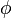 stammen aus dem Tafelwerk.
stammen aus dem Tafelwerk. 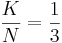 ;
;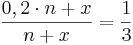 ;
;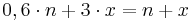 ;
;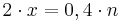 ;
;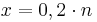 ;
;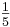 .
.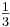 .
.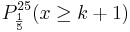
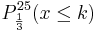
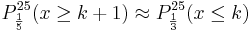
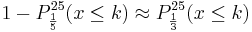
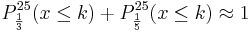
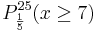
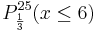
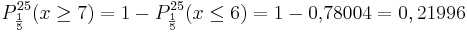
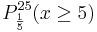
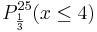

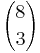 Möglichkeiten.
Möglichkeiten.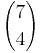 Möglichkeiten ergibt.
Möglichkeiten ergibt.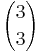
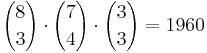 Möglichkeiten.
Möglichkeiten.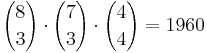
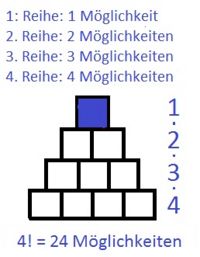
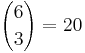 Möglichkeiten ergibt.
Möglichkeiten ergibt. 
