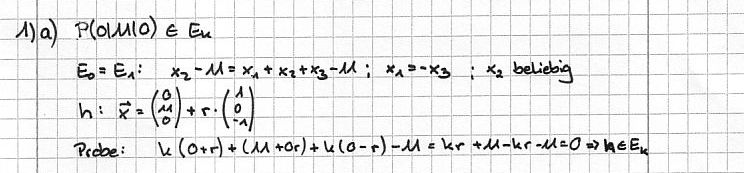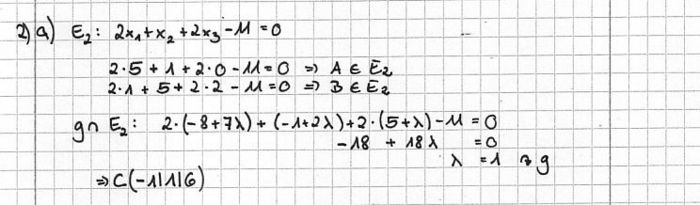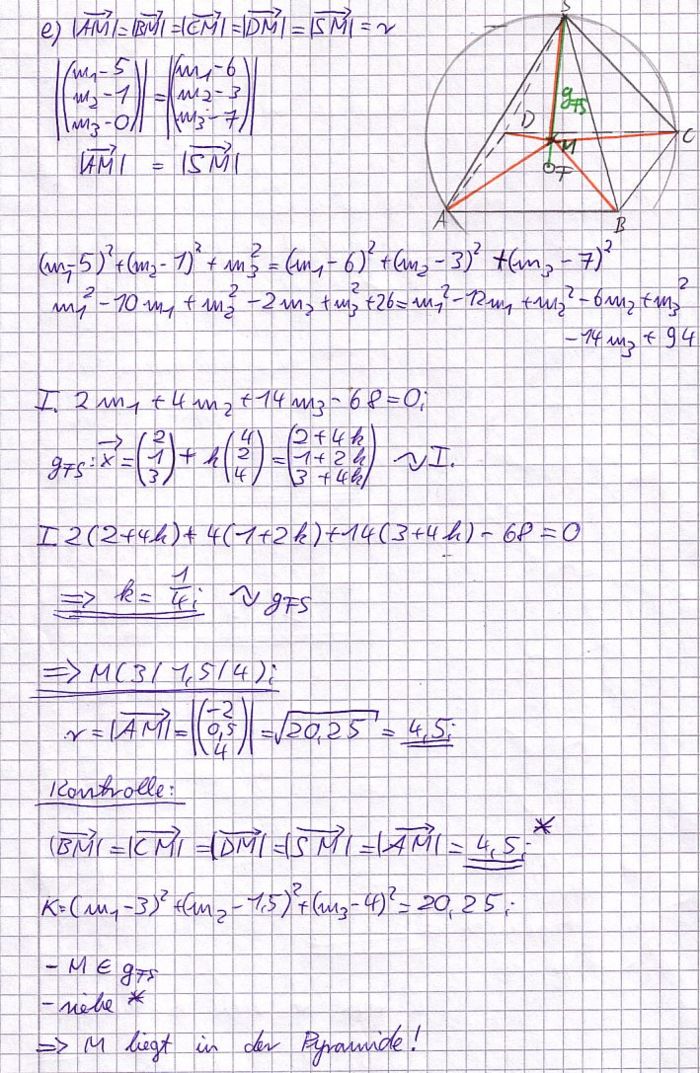- Aufgabe 2
a) Zeigen Sie, dass die Punkte A und B in der Ebene E2 liegen, und bestimmen Sie die Koordinaten des Schnittpunkts C von E2 mit der Geraden g. [Zur Kontrolle: C(−1|1| 6)]
- [Lösung anzeigen][Lösung ausblenden]
b) Weisen Sie nach, dass das Dreieck ABC gleichschenklig-rechtwinklig ist, und ermitteln Sie die Koordinaten eines Punkts D so, dass das Viereck ABCD ein Quadrat ist.
- [Lösung anzeigen][Lösung ausblenden]
Das Quadrat ABCD als Grundfläche bildet zusammen mit einem Punkt S als Spitze eine vierseitige Pyramide ABCDS. Der Punkt S liegt dabei auf der Geraden g und ist so gewählt, dass die Pyramide gerade ist, das heißt, der Fußpunkt F der Pyramidenhöhe ist gleichzeitig der Diagonalenschnittpunkt
des Quadrats.
c) Bestimmen Sie die Koordinaten der Punkte F und S. [Zur Kontrolle: S(6|3|7)]
- [Lösung anzeigen][Lösung ausblenden]
d) Ermitteln Sie das Volumen der Pyramide sowie den Inhalt ihrer Oberfläche.
- [Lösung anzeigen][Lösung ausblenden]
e) K sei die Kugel, auf der alle Ecken der Pyramide ABCDS liegen. Bestimmen Sie die Koordinaten des Mittelpunkts M und den Radius r der Kugel K und zeigen Sie, dass M im Inneren der Pyramide liegt.
- [Lösung anzeigen][Lösung ausblenden]
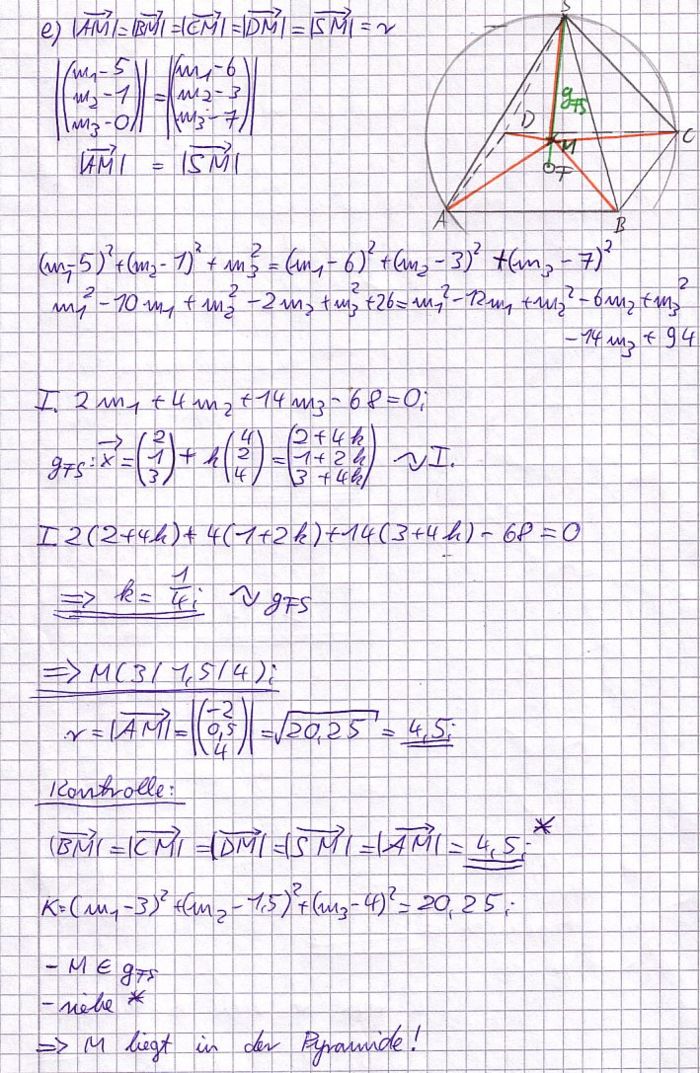
Alternativer Lösungsweg:

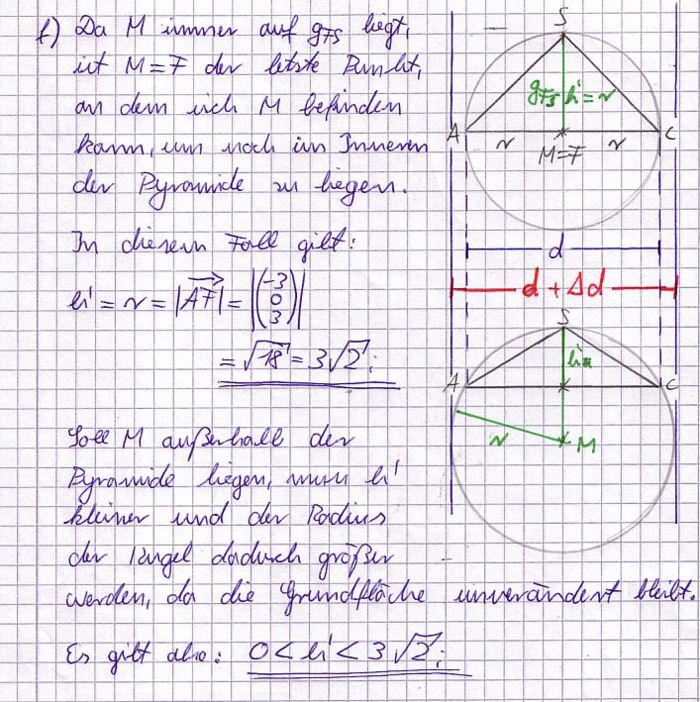
f) Betrachtet werden nun eine gerade Pyramide mit dem Quadrat ABCD als Grundfläche und der Höhe h' > 0 sowie die Kugel durch die Ecken dieser Pyramide. Für welche Werte von h' liegt der Mittelpunkt dieser Kugel außerhalb der Pyramide?
- [Lösung anzeigen][Lösung ausblenden]
| 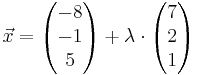 , λ ∈ IR sowie die Ebenenschar Ek : kx1 + x2 + kx3 −11 = 0 , k ∈ IR.
, λ ∈ IR sowie die Ebenenschar Ek : kx1 + x2 + kx3 −11 = 0 , k ∈ IR.