1.Die Funktion f(x)=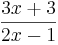 ist eine (!Lineare Funktion) (!Ganzrationale Funktion) (!Trigonometrische Funktion) (!Exponentialfunktion) (Gebrochen rationale Funktion)
ist eine (!Lineare Funktion) (!Ganzrationale Funktion) (!Trigonometrische Funktion) (!Exponentialfunktion) (Gebrochen rationale Funktion)
2. Eine Funktion, die keinen Grenzwert besitzt, ist (Divergent) (!Konvergent) (!Punktsymmetrisch zum Ursprung) (!Gebrochen rational)
3. Der Zusammenhang g(x)=f(-x) entspricht (!Einer Achsensymmetrie zur y-Achse) (!Einer Spiegelung an der x-Achse) (!Einer Punktsymmetrie zum Ursprung) (Einer Spiegelung an der y-Achse) (!Einer Streckung in x-Richtung)
4. Der abgebildete Graph der Funktion f(x)=x4-3x2+1 ist 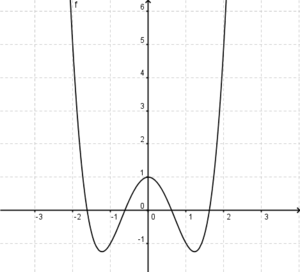 (!Punktsymmetrisch zum Ursprung) (Gerade) (Ganzrational) (!Quadratisch) (Achsensymmetrisch zur y-Achse) (!Ungerade) (Divergent) (!Konvergent)
(!Punktsymmetrisch zum Ursprung) (Gerade) (Ganzrational) (!Quadratisch) (Achsensymmetrisch zur y-Achse) (!Ungerade) (Divergent) (!Konvergent)
5. Der Funktionsterm der Funktion g(x), die von f(x)=2x4-x3 ausgehend um den Faktor 3 in y-Richtung getreckt und anschließend um 2 Einheiten nach oben verschoben wird, lautet (6x4-3x3+2) (!2[3x]4-[2x]3+2) (!6x4-3x3+6) (!5x4-3x3+1) (!6[x+2]4-3[x+2]3) (!6x4-3x3)
6. 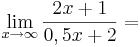 (!Unendlich) (!2) (!1) (!0) (4) (!-2) (!0,5)
(!Unendlich) (!2) (!1) (!0) (4) (!-2) (!0,5)
7. Der Graph der Funktion f(x)=2x2+1 ist gegenüber dem Graphen g(x)=x2-1 (!In y-Richtung Gestreckt und nach unten verschoben) (Nach oben verschoben ) (In y-Richtung gestreckt und in positiver y-Richtung verschoben ) (In y-Richtung gestreckt ) (!In negativer y-Richtung verschoben) (!Gar nicht verschoben) (!Gar nicht gestreckt)
8. Was trifft auf diese Funktion zu? f(x)=sinx (Punktsymmetrie zum Ursprung) (Trigonometrisch) (!Linear) (!Graph: Parabel) (!Keine Nullstellen) (!Achsensymmetrie zur y-Achse) (f[0]=0)
9. Bei einer Streckung in x-Richtung (!Verändert sich die Amplitude einer trigonometrischen Funktion) (Bleiben die Funktionswerte an der Stelle x=0 unverändert ) (!Bleiben die Nullstellen unverändert) (!Wird der Graph an der x-Achse gespiegelt) (Erfolgt die Streckung um den Faktor 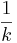 )
)
10. Um einen Graphen an der y-Achse zu spiegeln (!Multipliziert man den Funktionsterm mit -1) (Setzt man für f[x] f[-x]ein ) (Schreibt man vor jedes x ein „Minus“ ) (!Verschiebt man den Graphen nach rechts oder links [je nach Lage])
11. Um was für eine Funktion handelt es sich? 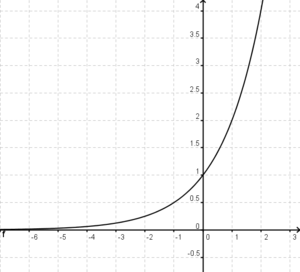 (Exponentialfunktion) (!Lineare Funktion ) (!Trigonometrische Funktion) (!Gebrochen rationale Funktion)
(Exponentialfunktion) (!Lineare Funktion ) (!Trigonometrische Funktion) (!Gebrochen rationale Funktion)
12. 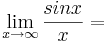 (!Existiert nicht) (!Unendlich) (0)(!1)
(!Existiert nicht) (!Unendlich) (0)(!1)
13. Wie lautet der Funktionsterm der Funktion g(x), die von f(x)=x3+x2-1 ausgehend zwei Einheiten weiter rechts verläuft? (![x+2]3+[x+2]2-1) (!x3+x2+1) ([x-2]3+[x-2]2-1) (!x3+x2-3) (x3-5x2+8x-5) (!x3+5x2-8x+5)