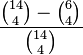Abi 2016 Stochastik II Teil A

Mathematik (Bayern): Abiturprüfung 2016 Stochastik II - Teil A Download der Originalaufgaben - Lösung zum Ausdrucken

Aufgabe 1 Bei einem Zufallsexperiment wird eine ideale Münze so lange geworfen, bis zum zweiten Mal Zahl (Z) oder zum zweiten Mal Wappen (W) oben liegt. Als Ergebnismenge wird festgelegt: {ZZ; WW; ZWZ; ZWW; WZZ; WZW}. a) Begründen Sie, dass dieses Zufallsexperiment kein Laplace-Experiment ist. b) Die Zufallsgröße X ordnet jedem Ergebnis die Anzahl der entsprechenden Münzwürfe zu. Berechnen Sie den Erwartungswert von X. [Lösung anzeigen][Lösung ausblenden] 700px

Aufgabe 2 An einem P-Seminar nehmen acht Mädchen und sechs Jungen teil, darunter Anna und Tobias. Für eine Präsentation wird per Los aus den Teilnehme- rinnen und Teilnehmern ein Team aus vier Personen zusammengestellt. a) Geben Sie zu jedem der folgenden Ereignisse einen Term an, mit dem die Wahrscheinlichkeit des Ereignisses berechnet werden kann. A: „Anna und Tobias gehören dem Team an.“ B: „Das Team besteht aus gleich vielen Mädchen und Jungen.“ b) Beschreiben Sie im Sachzusammenhang ein Ereignis, dessen Wahrscheinlichkeit durch den folgenden Term berechnet werden kann: $\frac{\binom{14}{4}-\binom{6}{4}}{\binom{14}{4}}$ [Lösung anzeigen][Lösung ausblenden] 700px