Abi 2016 Analysis II Teil A
|
|
1) Gegeben ist die Funktion
|
2) Geben Sie jeweils den Term und den Definitionsbereich einer Funktion an, die die angegebene(n) Eigenschaft(en) besitzt.
|
3) Abbildung 1 zeigt den Graphen der in IR definierten Funktion f. a) Bestimmen Sie mithilfe von Abbildung 1 einen Näherungswert für
|
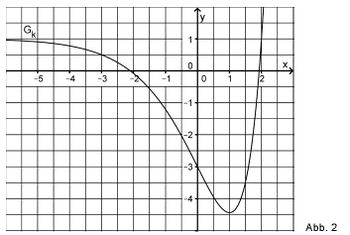
4) Abbildung 2 zeigt den Graphen Gk einer in IR definierten Funktion k. Skizzieren Sie in Abbildung 2 den Graphen der zugehörigen Ableitungsfunktion k'. Berücksichtigen Sie dabei insbesondere einen Näherungswert für die Steigung des Graphen Gk an dessen Wendepunkt ( 0 | -3 ) sowie die Nullstelle von k'. |
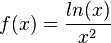 mit maximalem Definitionsbereich D.
mit maximalem Definitionsbereich D. 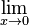 f(x).
f(x). 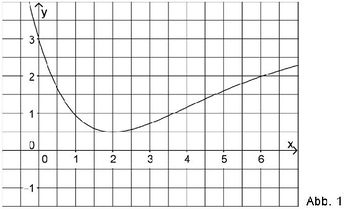
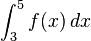 .
. 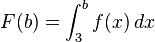 mit b ∈ IR gilt.
mit b ∈ IR gilt.