Abi 2013 Geometrie II Teil B
|
|
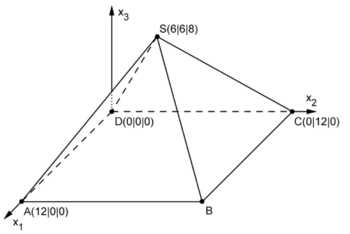
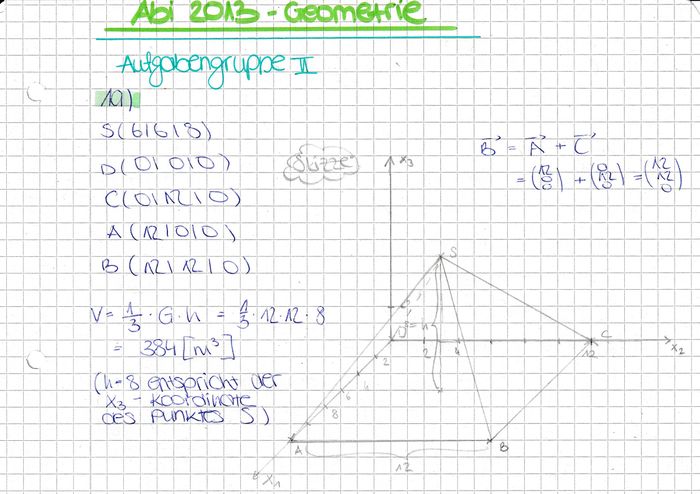
Die Abbildung zeigt modellhaft einen Ausstellungspavillon, der die Form einer geraden vierseitigen Pyramide mit quadratischer Grundfläche hat und auf einer horizontalen Fläche steht. Das Dreieck BCS beschreibt im Modell die südliche Außenwand des Pavillons. Im Koordinatensystem entspricht eine Längeneinheit 1m, d. h. die Grundfläche des Pavillons hat eine Seitenlänge von 12 m.
b) Die südliche Außenwand des Pavillons liegt im Modell in einer Ebene E. Bestimmen Sie eine Gleichung von E in Normalenorm.
c) Der Innenausbau des Pavillons erfordert eine möglichst kurze, dünne Strebe zwischen dem Mittelpunkt der Grundfläche und der südlichen Außenwand. Ermitteln Sie, in welcher Höhe über der Grundfläche die Strebe an der Außenwand befestigt ist. An einem Teil der südlichen Außenwand sind Solarmodule flächenbündig montiert. Die Solarmodule bedecken im Modell eine dreieckige Fläche, deren Eckpunkte die Spitze S sowie die Mittelpunkte der Kanten [SB] und [SC] sind. d) Ermitteln Sie den Inhalt der von den Solarmodulen bedeckten Fläche. e)
Die von Solarmodulen abgegebene elektrische Leistung hängt unter an- derem von der Größe ihres Neigungswinkels gegen die Horizontale ab. Die Tabelle gibt den Anteil der abgegebenen Leistung an der maximal möglichen Leistung in Abhängigkeit von der Größe des Neigungswinkels an. Schätzen Sie diesen Anteil für die Solarmodule des Pavillons - nach Berechnung des Neigungswinkels - unter Verwendung der Tabelle ab.
|
|
2)
In einem kartesischen Koordinatensystem sind die Geraden a) Bestimmen Sie die Koordinaten von T.
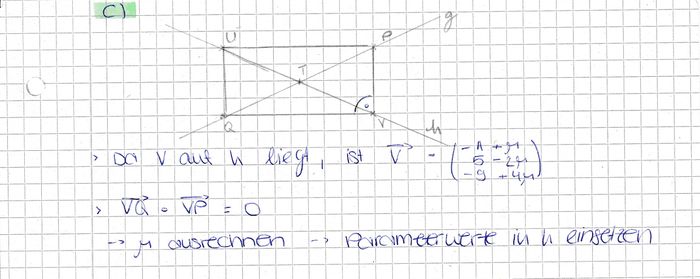
b)Geben Sie die Koordinaten zweier Punkte P und Q an, die auf g liegen und von T gleich weit entfernt sind. c) Zwei Punkte U und V der Geraden h bilden zusammen mit P und Q das Rechteck PUQV. Beschreiben Sie einen Weg zur Ermittlung der Koordinaten von U und V. |




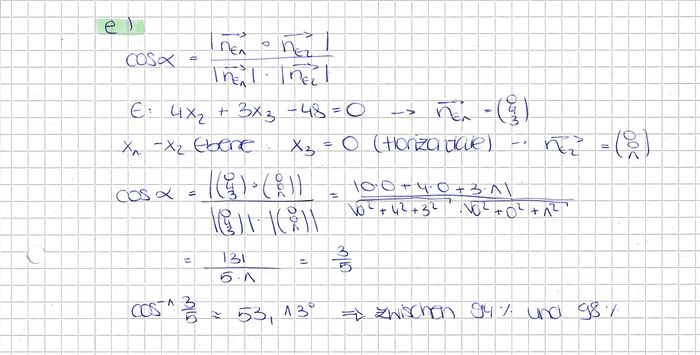
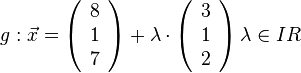 und
und 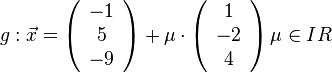 gegben.
gegben.