Ähnlichkeit - Übung 4
Aus RMG-Wiki
Version vom 28. Januar 2009, 19:40 Uhr von Bendel Julia (Diskussion | Beiträge)
Aufgabe 1
Aufgabe:
Stelle fest, ob die Dreiecke ABC und A'B'C' ähnlich sind, wenn:
a) a = 5; b = 8; c = 10 und a' = 2,5; b' = 4; c' = 5
b)  = 30°;
= 30°; 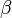 = 100° und
= 100° und 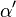 = 50°;
= 50°; 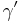 = 100°
= 100°
c) a = 5; c = 8; 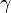 = 100° und b' = 2,5; c' = 4;
= 100° und b' = 2,5; c' = 4; 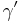 = 100°
= 100°
Tipp: Wenn du unsicher bist kann dir eine Skizze helfen, in der du die gegebenen Seiten bzw. Winkel farbig markierst!
a) Die beiden Dreiecke sind ähnlich, da sie im Verhältnis ihrer Seiten übereinstimmen (S : S : S - Satz).
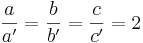
b) Die beiden Dreiecke sind ähnich, da sie in zwei Winkeln übereinstimmen (WW - Satz).
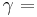 180° - (
180° - ( +
+ 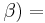 180° - (30° + 100°)
180° - (30° + 100°)  50°
50° 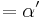
c)

Aufgabe 2
Aufgabe:
Aufgabe 3
Aufgabe: