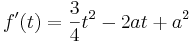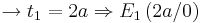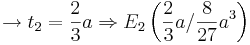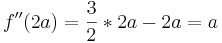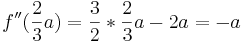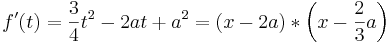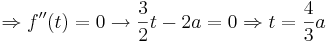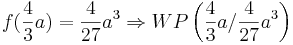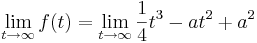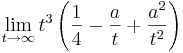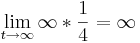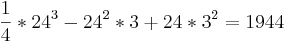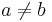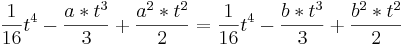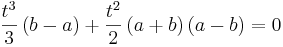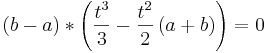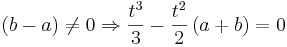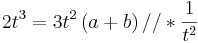LK Mathematik Abitur NRW 2007: Unterschied zwischen den Versionen
(Verbesserungen) |
(Verbesserungen) |
||
| Zeile 68: | Zeile 68: | ||
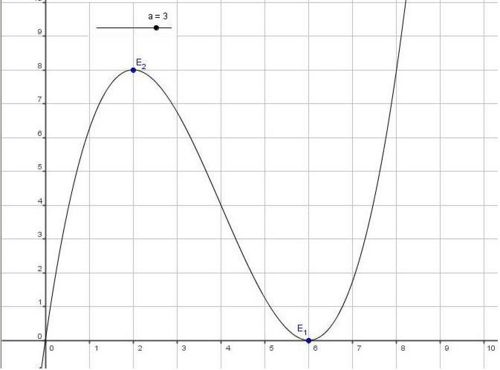
| − | ::Am Schönsten sind die Extremwerte für a = 3 zu errechnen und graphisch zu sehen, da sich die Koordinaten <math>E_1</math> ( 6 / 0 ) und <math>E_2</math> ( 2 / 8 ) ergeben. | + | ::Am Schönsten sind die Extremwerte für a = 3 zu errechnen und graphisch zu sehen, da sich die Koordinaten |
| + | |||
| + | ::<math>E_1</math> ( 6 / 0 ) und <math>E_2</math> ( 2 / 8 ) ergeben. | ||
<popup name="Funktionsgraph für a = 3"> | <popup name="Funktionsgraph für a = 3"> | ||
| Zeile 79: | Zeile 81: | ||
| − | :Lösung 1: ''Krümmungsverhalten an den Extremwerten'' | + | :<u>'''Lösung 1:''' ''Krümmungsverhalten an den Extremwerten''</u> |
| − | :Dazu setzt man einfach die t - Koordinate in die zweite Ableitung ein. Wird die zweite Ableitung größer Null ist es ein Minimum und die Funktion ist linksgekrümmt, dass heißt es handelt sich um eine "Linkskurve". Ist die zweite Ableitung hingegen | + | :Dazu setzt man einfach die t - Koordinate in die zweite Ableitung ein. Wird die zweite Ableitung '''größer Null''' ist es ein '''Minimum''' und die Funktion ist '''linksgekrümmt''', dass heißt es handelt sich um eine "Linkskurve". Ist die zweite Ableitung hingegen '''kleiner Null''', handelt es sich um eine '''Rechtskrümmung''' und um ein '''Maximum'''. Wäre die zweite Ableitung ''gleich Null'', handelt es sich bei dem Extremwert um einen ''Terassenpunkt'', dass heißt, dass die Steigung der Funktion ''keinen Vorzeichenwechsel an dieser Stelle'' hat. |
| − | ''<span style="color: darkblue">Gib mit dieser Lösungsmöglichkeit die Art der Extremwerte an.</span> | + | ::''<span style="color: darkblue">Gib mit dieser Lösungsmöglichkeit die Art der Extremwerte an.</span> |
::{{Lösung versteckt|1= | ::{{Lösung versteckt|1= | ||
| Zeile 101: | Zeile 103: | ||
| − | : | + | :<u>'''Lösung 2:''' ''h - Methode''</u> |
| + | |||
| + | :Mit Hilfe der h - Methode untersucht man, wie sich der Graph "ein Stückchen links und ein Stückchen rechts" vom Extremwert verhält. Dazu nimmt man die erste Ableitung, setzt einmal f '(<math>2a - h</math>) und einmal f '(<math>2a + h</math>) ein, um das Verhalten von G<sub>f</sub> für t < 2a bzw t > 2a zu bestimmen. Ergibt sich hier je ein positiver und ein negativer Wert, weiß man, dass es sich um einen Extremwert handelt. Ist beispielsweise f '(<math>t_1 - h</math>) < 0 und f '(<math>t_1 + h</math>) > 0, dann liegt ein Minimum vor, da links vom Extremwert der Graph fällt, und rechts steigt. Wenn sich zweimal das gleiche Vorzeichen für t < 2a bzw t > 2a ergeben sollte, dann handelt es sich um keinen direkten Extremwert, sondern um einen, wie bereits in Lösung 1 beschriebenen, Terassenpunkt. | ||
| + | |||
| + | ::<span style="color: darkblue">Versuche auch, mit Hilfe der h - Methode, die Art der Extrempunkte zu bestimmen.</span> | ||
| Zeile 110: | Zeile 116: | ||
| − | Daraus ergibt sich nun folgendes Monotonieverhalten. | + | Daraus ergibt sich nun folgendes, graphisches Monotonieverhalten. |
<ggb_applet width="700" height="600" filename="Monotonie.ggb" showResetIcon="true" /> | <ggb_applet width="700" height="600" filename="Monotonie.ggb" showResetIcon="true" /> | ||
| Zeile 121: | Zeile 127: | ||
| − | : | + | :<u>'''Lösung 3:''' ''Vorzeichentabelle''</u> |
| + | |||
| + | :Man schreibt die Ableitung nicht als Summen, sondern als Produkte. Da mann die Nullstellen der ersten Ableitung kennt, kann man dies machen. Allgemein würde es heißen | ||
::<math>f '(t)= \left( x - t_1 \right) * \left( x - t_2 \right)</math>, | ::<math>f '(t)= \left( x - t_1 \right) * \left( x - t_2 \right)</math>, | ||
| − | : | + | :wobei t<sub>1</sub> und t<sub>2</sub> die t - Werte des Extrempunktes sind. |
| − | : | + | :Nun stellt man eine Vorzeichentabelle auf, für jeden Faktor und erhält durch multiplizieren der Vorzeichen das Monotonieverhalten und die Arten der Extremwerte. |
| + | ::<span style="color: darkblue">Zerlege die Ableitung in ein Produkt und verdeutliche mit Hilfe einer Vorzeichentabelle die Art der Extremwerte. </span> | ||
| + | |||
::{{Lösung versteckt|1= | ::{{Lösung versteckt|1= | ||
::<math>f '(t) = \frac{3}{4} t^2 - 2 a t + a^2 = \left( x - 2a \right) * \left( x - \frac{2}{3}a \right) </math> | ::<math>f '(t) = \frac{3}{4} t^2 - 2 a t + a^2 = \left( x - 2a \right) * \left( x - \frac{2}{3}a \right) </math> | ||
Version vom 8. Januar 2010, 16:00 Uhr
Inhaltsverzeichnis |
Was ist eine Funktion ?
|
So wie im täglichen Leben Statistiken oder Tabellen erstellt werden, können auch in der Mathematik sogenannte Funktionen erstellt werden. Diese sind, ähnlich wie bei einer Tabelle, abhängig von zwei meist unterschiedlichen Größen. Bei den mathematischen Funktionen ist es so, dass einer bestimmten Menge auf der x – Achse, eine bestimmte Menge auf der y - Achse zugeordnet wird. Bei rein mathematischen Überlegungen handelt es sich bei den beiden Mengen um den sogenannten x – Wert beziehungsweise y – Wert. Bei Funktionen mit Einheiten, wie zum Beispiel in der Physik der „Waagrechte Wurf“, wird dem x – Wert die Einheit Länge in Meter gegeben und dem y – Wert Höhe in Meter zugeteilt. Jedoch ist zu beachten, dass bei Funktionen jedem x - Wert nur ein y – Wert zugeordnet werden kann. Es ist also nicht möglich, dass eine Funktion mit dem x – Wert x1 zwei y – Werte y1 und y2 hat. Der Unterschied zwischen einer Funktion und einer Wertetabelle ist lediglich, dass die Funktion eine graphische Abbildung der Wertetabelle darstellt. |
Angabe
Mit Hilfe der folgenden Funktion kann man beispielsweise die Wasserstände eines Flusses vorherzusagen. Diese Beschreibung der Durchflussgeschwindigkeit sei durch die Funktionenschar fa mit 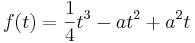 , a > 0
, a > 0
Die Funktion gibt dabei die Durchflussgeschwindigkeit in 106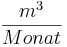 und t die verstrichene Zeit in Monaten seit Beginn der Vorhersage
und t die verstrichene Zeit in Monaten seit Beginn der Vorhersage
(t = 0) an. Die Funktion berücksichtigt, dass es sich um einen Fluss handelt, der zeitweise austrocknet.
Aufgabe: Nullstellen
Es soll bestimmt werden, abhängig vom Parameter a, zu welchen Monaten kein Wasser durch den Fluss fließt.
Es sind die Zeitpunkte gesucht, an denen der y - Wert Kubikmeter in Millionen gleich Null ist. An dieser Nullstelle fließt also kein Wasser durch den Fluss. Folglich ist fa (t) = 0 zu setzen.
- Was fällt auf, wenn man mit Hilfe des Schiebereglers den Parameter a verändert?
- Jede Funktion
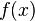 , unabhängig vom Parameter a, schneidet den Ursprung. Das ist die erste Nullstelle, welche der Graph besitzt. Sie ist also unabhänig von a Dies kann man leicht aus der Funktion ablesen, da man eben diese Nullstelle durch einfaches Ausklammern erhält.
, unabhängig vom Parameter a, schneidet den Ursprung. Das ist die erste Nullstelle, welche der Graph besitzt. Sie ist also unabhänig von a Dies kann man leicht aus der Funktion ablesen, da man eben diese Nullstelle durch einfaches Ausklammern erhält.
- Die andere Nullstelle wird mit wachsendem Parameter a immer weiter vom Ursprung entfernt. Sie ist also abhängig von a. Sie ist, wie man im Applet sieht, eine doppelte Nullstelle, was heißt, dass sie an der Stelle einen Vorzeichenwechsel bezüglich der Steigung besitzt. Sie schneidet nicht die t - Achse, sie berührt sie nur. Löst man die Quadratische Gleichung mit Hilfe der Mitternachtsformel erhält man die zweite Nullstelle.
- Der Fluss trocknet zu den Zeitpunkten t = 0 und t = 2a aus, es fließt also kein Wasser durch den Fluss.
Aufgabe: Extremwerte
Es soll, in Abhängigkeit von a, ermittelt werden, zu welchen Zeitpunkten t ein relatives Maximum bzw. Minimum vorliegt. Diese Funktionswerte sollen berechnet werden.
Maxima und Minima sind Punkte auf einer Funktion, die in ihrem im Umkreis die höchsten beziehungsweise tiefsten Punkte auf dem Graphen sind. Um diese Extremwerte einer Funktion zu errechnen, wird die erste Ableitung benötigt.
|
Die allgemeine Ableitungsregel ist: |
- Bestimme nun die erste Ableitung der Funktion
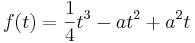
- Bestimme nun die erste Ableitung der Funktion
- Errechne nun die Koordinaten der Extremwerte.
- Um die t - Werte der Extremwerte zu erhalten, setzt man die Funktion f '(t) = 0. Da man nun eine quadratischen Gleichung bekommt, kann man, mit Hilfe der "Mitternachtsformel", die beiden Lösungen ausrechnen. Schließlich setzt man die errechneten t - Werte in die Funktion ein und erhält somit die y - Koordinaten der Extremwerte E1 und E2.
- Am Schönsten sind die Extremwerte für a = 3 zu errechnen und graphisch zu sehen, da sich die Koordinaten
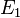 ( 6 / 0 ) und
( 6 / 0 ) und 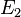 ( 2 / 8 ) ergeben.
( 2 / 8 ) ergeben.
Man hat nun die Extremwerte in Abhängigkeit von a ermittelt. Um nun zu prüfen ob es sich bei den Extrema um Maxima oder Minima handelt, kann man hier anhand verschiedener Lösungen vorgehen.
- Lösung 1: Krümmungsverhalten an den Extremwerten
- Dazu setzt man einfach die t - Koordinate in die zweite Ableitung ein. Wird die zweite Ableitung größer Null ist es ein Minimum und die Funktion ist linksgekrümmt, dass heißt es handelt sich um eine "Linkskurve". Ist die zweite Ableitung hingegen kleiner Null, handelt es sich um eine Rechtskrümmung und um ein Maximum. Wäre die zweite Ableitung gleich Null, handelt es sich bei dem Extremwert um einen Terassenpunkt, dass heißt, dass die Steigung der Funktion keinen Vorzeichenwechsel an dieser Stelle hat.
- Gib mit dieser Lösungsmöglichkeit die Art der Extremwerte an.
- Die zweite Ableitung lautet:
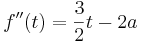
- Die zweite Ableitung lautet:
- da a > 0
 Rechtskrümmung
Rechtskrümmung 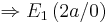 ist Minimum
ist Minimum
- da a > 0
- da a größer als Null definiert ist, gilt
 - (a) < 0
- (a) < 0  Linkskrümmung
Linkskrümmung 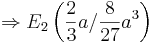 ist Maximum
ist Maximum
- da a größer als Null definiert ist, gilt
- Lösung 2: h - Methode
- Mit Hilfe der h - Methode untersucht man, wie sich der Graph "ein Stückchen links und ein Stückchen rechts" vom Extremwert verhält. Dazu nimmt man die erste Ableitung, setzt einmal f '(
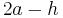 ) und einmal f '(
) und einmal f '(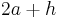 ) ein, um das Verhalten von Gf für t < 2a bzw t > 2a zu bestimmen. Ergibt sich hier je ein positiver und ein negativer Wert, weiß man, dass es sich um einen Extremwert handelt. Ist beispielsweise f '(
) ein, um das Verhalten von Gf für t < 2a bzw t > 2a zu bestimmen. Ergibt sich hier je ein positiver und ein negativer Wert, weiß man, dass es sich um einen Extremwert handelt. Ist beispielsweise f '(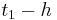 ) < 0 und f '(
) < 0 und f '(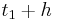 ) > 0, dann liegt ein Minimum vor, da links vom Extremwert der Graph fällt, und rechts steigt. Wenn sich zweimal das gleiche Vorzeichen für t < 2a bzw t > 2a ergeben sollte, dann handelt es sich um keinen direkten Extremwert, sondern um einen, wie bereits in Lösung 1 beschriebenen, Terassenpunkt.
) > 0, dann liegt ein Minimum vor, da links vom Extremwert der Graph fällt, und rechts steigt. Wenn sich zweimal das gleiche Vorzeichen für t < 2a bzw t > 2a ergeben sollte, dann handelt es sich um keinen direkten Extremwert, sondern um einen, wie bereits in Lösung 1 beschriebenen, Terassenpunkt.
- Versuche auch, mit Hilfe der h - Methode, die Art der Extrempunkte zu bestimmen.
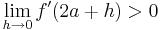 und
und 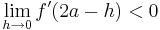
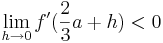 und
und 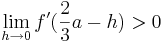
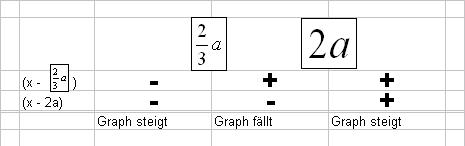
Daraus ergibt sich nun folgendes, graphisches Monotonieverhalten.
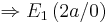 ist Minimum
ist Minimum
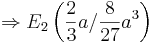 ist Maximum
ist Maximum
- Lösung 3: Vorzeichentabelle
- Man schreibt die Ableitung nicht als Summen, sondern als Produkte. Da mann die Nullstellen der ersten Ableitung kennt, kann man dies machen. Allgemein würde es heißen
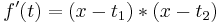 ,
,
- wobei t1 und t2 die t - Werte des Extrempunktes sind.
- Nun stellt man eine Vorzeichentabelle auf, für jeden Faktor und erhält durch multiplizieren der Vorzeichen das Monotonieverhalten und die Arten der Extremwerte.
- Zerlege die Ableitung in ein Produkt und verdeutliche mit Hilfe einer Vorzeichentabelle die Art der Extremwerte.
Aufgabe: Wendepunkt
Es soll, in Abhängigkeit von a bestimmt werden, wann die Druchflussgeschwindigkeit besonders stark absinkt. Dieser Wert soll zum Zeitpunkt t berechnet werden.
Dazu schaut man sich die erste Ableitung näher an. Diese zeigt einem die Steigung des Graphen Gf.
Da es sich bei der ersten Ableitung um eine nach oben geöffnete Parabel handelt, ist das Minimum des Graphen gleichzeitig der Punkt, an dem die Steigung besonders stark abfällt. Wenn man von der Funktion f (t) ausgeht, ist der gesuchte Punkt der Wendepunkt. An ihm besitzt der Graph Gf den größten negativen Wert. Errechne diesen Wert.
- Der Punkt, an welchem die Funktion besonders stark abfällt ist zugleich der Wendepunkt
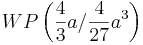
- Der Punkt, an welchem die Funktion besonders stark abfällt ist zugleich der Wendepunkt
Aufgabe: Theoretische Überlegungen zur Funktion
Warum liegt kein Punkt der Funktionsgraphen von fa im Bereich 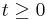 unterhalb der t - Achse und inwiefern ist dies mit dem zugrunde liegenden Sachverhalt vereinbar.
unterhalb der t - Achse und inwiefern ist dies mit dem zugrunde liegenden Sachverhalt vereinbar.
Begründe dies.
- Es liegt kein Punkt im Intervall
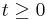 unterhalb der t - Achse, da es hier um eine Funktion mit realem Bezug geht. Läge ein Punkt bei der gegebenen Aufgabenstellung im vierten Quadranten, würde dies bedeuten, dass eine negative Durchflussgeschwindigkeit vorliegen würde. Dies ist nicht möglich, da es heißen würde, dass ein negatives Volumen an Wasser im Fluss ist. Deshalb ist kein Punkt der Funktionsgraphen fa im vierten Quadranten definiert.
unterhalb der t - Achse, da es hier um eine Funktion mit realem Bezug geht. Läge ein Punkt bei der gegebenen Aufgabenstellung im vierten Quadranten, würde dies bedeuten, dass eine negative Durchflussgeschwindigkeit vorliegen würde. Dies ist nicht möglich, da es heißen würde, dass ein negatives Volumen an Wasser im Fluss ist. Deshalb ist kein Punkt der Funktionsgraphen fa im vierten Quadranten definiert.
- Es liegt kein Punkt im Intervall
Es soll das Verhalten von fa für 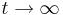 angegeben werden. Des Weiteren soll begründet werden, ob die Funktionen auch nach den ersten 8 Monate noch eine sinnvolle Beschreibung der Durchflussgeschwindigkeit liefern.
angegeben werden. Des Weiteren soll begründet werden, ob die Funktionen auch nach den ersten 8 Monate noch eine sinnvolle Beschreibung der Durchflussgeschwindigkeit liefern.
- (Höchste Potenz ausklammern!)
- Für
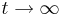 geht die Funktion gegen +
geht die Funktion gegen + 
- Für
- Nach den ersten 8 Monaten verhält sich die Funktion so, dass sie immer stärker ansteigt. Dies ist an der Parabel, welche die Steigung anzeigt, erkennbar. Da die Funktion fa (t) vorhersagen soll, wieviel Wasser sich zu einem Zeitpunkt t im Wasser befindet. Wenn man nun, anhand der Funktion vorhersagen soll, wieviel Wasser in zwei Jahren ( also 24 Monaten ) ergibt sich ein Wasserstandswert, der mit sehr hoher Wahrscheinlichkeit nicht erreicht werden wird.
- Nehmen wir nun mal das Beispiel t = 24 und a = 3.
- Da das Ergebnis in Millionenkubikmeter pro Monat angegeben ist, wäre dann der Wert
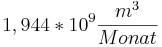 . Dieser Wasserstandswert wäre eine ziemlich grobe Abweichung vom Realwert. Aus diesem Grund handelt es sich bei der Funktion eher um eine Sinusähnliche Funktion, als um eine, die gen Unendlich exponential ansteigt. Dies würde heißen, dass das zweite Austrocknen auf der t - Achse verschoben wird, wieder als t = 0 definiert werden würde, und die Funktion fa (t) wieder von vorne starten würde.
. Dieser Wasserstandswert wäre eine ziemlich grobe Abweichung vom Realwert. Aus diesem Grund handelt es sich bei der Funktion eher um eine Sinusähnliche Funktion, als um eine, die gen Unendlich exponential ansteigt. Dies würde heißen, dass das zweite Austrocknen auf der t - Achse verschoben wird, wieder als t = 0 definiert werden würde, und die Funktion fa (t) wieder von vorne starten würde.
- Da das Ergebnis in Millionenkubikmeter pro Monat angegeben ist, wäre dann der Wert
Aufgabe: Flächenberechnung einer Funktion
Ermittle für a = 3, wie viel Liter Wasser in den ersten sechs Monaten durch den Fluss fließen.
Dazu wird die Funktion gesucht, deren Ableitung die Funktion fa (t) ist. Gebe diese Funktion an und errechne mit ihr für a = 3, wieviel Liter durch den Fluss geflossen sind.
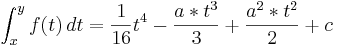
Die obere Grenze ist: 6 Nach den ersten sechs Monaten
Die untere Grenze ist: 0
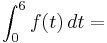
![\left[ \frac{1}{16}t^4 - \frac{3*t^3}{3} + \frac{3^2*t^2}{2}\right ]_{0}^{6} = 27 - 0 = 27](/images/math/4/9/a/49a1f445fbc0fa11cad513f8131a8bd7.png)
Aufgabe: Flächengleichheit zweier Funktionen
Betrachte nun zwei unterschiedliche Funktionen fa1 und fa2. Es soll der Zeitpunkt bestimmt werden, zu dem für beide Funktionsannahmen (seit t = 0) genau gleich viel Wasser durch den Fluss geflossen wäre.
Dazu werden zwei Integralfunktionen Fa1 und Fa2 gleichgesetzt und so weit wie möglich nach t aufgelöst.
- Im Weiteren wird eine Funktion mit Parameter a, die andere mit Parameter b bezeichnet. Wobei gilt:
- Fa (t) = Fb (t)

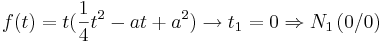
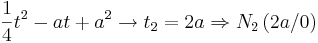

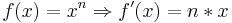 n-1
n-1