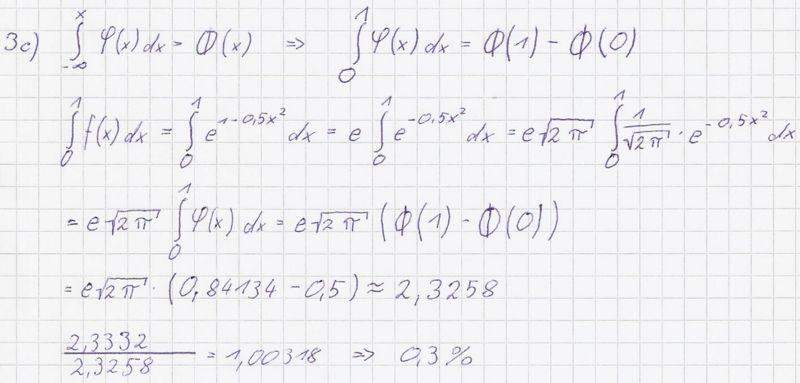2008 II: Unterschied zwischen den Versionen
(→Aufgabe 2) |
|||
| (7 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | |
| − | + | ||
| − | |||
| − | == | + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> |
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | <center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung 2008'''</big></center> | ||
| + | <center><big>'''Infinitesimalrechnung II'''</big></center> | ||
| + | |||
| + | |||
| + | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=6765c5a90ce67dce2877992c3f4e2d9f '''Download der Originalaufgaben: Abitur 2008 LK Mathematik Bayern'''] | ||
| + | <br />Erstellt von Alistair Mainka und Benjamin Schleicher.</center> | ||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 1 | ||
Gegeben ist die Funktion <math>f(x)=e^{1-0,5x^2}</math> mit Definitionsbereich D<sub>f</sub> = IR . | Gegeben ist die Funktion <math>f(x)=e^{1-0,5x^2}</math> mit Definitionsbereich D<sub>f</sub> = IR . | ||
Die Abbildung auf der folgenden Seite zeigt den Graphen G<sub>f</sub> von f. | Die Abbildung auf der folgenden Seite zeigt den Graphen G<sub>f</sub> von f. | ||
| − | |||
a) Untersuchen Sie G<sub>f</sub> rechnerisch auf Symmetrie und Schnittpunkte mit | a) Untersuchen Sie G<sub>f</sub> rechnerisch auf Symmetrie und Schnittpunkte mit | ||
| Zeile 20: | Zeile 37: | ||
Koordinaten der Wendepunkte. (6BE) | Koordinaten der Wendepunkte. (6BE) | ||
| − | {{Lösung versteckt|[[Bild:ABI_2008_II_A1b_Lös1.jpg|800px]]}} | + | {{Lösung versteckt|[[Bild:ABI_2008_II_A1b_Lös1.jpg|800px]]}}<br /> |
| + | <popup name="Fragen"> | ||
| + | * Nur eine Kleinigkeit: ist f nicht streng monoton steigend für x<math>\le</math>0 (anstatt x<0), analog streng monoton fallend für x<math>\ge</math>0 ? | ||
| + | </popup> | ||
| − | + | </td></tr></table></center> | |
| − | |||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 2 | ||
| + | |||
| + | Die Integralfunktion F ist definiert durch <math>F(x)=\int_{0}^{x} f (t)\,dt</math>, x ∈ IR. | ||
a) Untersuchen Sie das Symmetrie-, Monotonie- und Krümmungsverhalten | a) Untersuchen Sie das Symmetrie-, Monotonie- und Krümmungsverhalten | ||
| Zeile 34: | Zeile 63: | ||
ein. (8BE) | ein. (8BE) | ||
| − | {{Lösung versteckt|[[Bild:ABI_2008_II_A2a_Lös1.jpg|800px]]}} | + | {{Lösung versteckt|[[Bild:ABI_2008_II_A2a_Lös1.jpg|800px]]}}<br /> |
| − | + | '''Könnt ihr die Abbildung mit dem eingezeichneten Graphen von F noch hochladen?''' | |
b) Für x > 1 gilt offensichtlich | b) Für x > 1 gilt offensichtlich | ||
| Zeile 42: | Zeile 71: | ||
Was folgt für die Funktionswerte von F für x ≥ 4? (5BE) | Was folgt für die Funktionswerte von F für x ≥ 4? (5BE) | ||
| − | {{Lösung versteckt|[[Bild:ABI_2008_II_A2b_Lös1.jpg|800px]] | + | {{Lösung versteckt|[[Bild:ABI_2008_II_A2b_Lös1.jpg|800px]] |
| + | '''Bemerkung:'''<br> | ||
| + | Zweiter Teil der Aufgabe fehlt: Funktionswerte von F(x) für x ≥ 4 sind sehr klein, F(x) liegt nur noch minimal über x-Achse. | ||
| + | }} | ||
| − | == | + | |
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 3 | ||
Die Funktion f soll im Folgenden in einer Umgebung von x = 0 durch eine | Die Funktion f soll im Folgenden in einer Umgebung von x = 0 durch eine | ||
| − | Polynomfunktion p mit dem Term <math>p(x) = | + | Polynomfunktion p mit dem Term <math>p(x) = ax^4 + bx^2 + c</math> , a, b, c ∈ IR , |
angenähert werden. | angenähert werden. | ||
| Zeile 56: | Zeile 99: | ||
Ohne Nachweis darf verwendet werden: <math>f '''(0) = 0, f ''''(0) = 3e</math> (6BE) | Ohne Nachweis darf verwendet werden: <math>f '''(0) = 0, f ''''(0) = 3e</math> (6BE) | ||
| − | [Zur Kontrolle: <math>p(x) = e(\frac{1}{8}x - \frac{1}{2} | + | [Zur Kontrolle: <math>p(x) = e \cdot (\frac{1}{8}x^4 - \frac{1}{2} x^2 + 1)</math>] |
{{Lösung versteckt|[[Bild:ABI_2008_II_A3a_Lös1.jpg|800px]]}} | {{Lösung versteckt|[[Bild:ABI_2008_II_A3a_Lös1.jpg|800px]]}} | ||
| − | |||
b) Zeigen Sie, dass p keine Nullstelle besitzt. Berechnen Sie den Inhalt A | b) Zeigen Sie, dass p keine Nullstelle besitzt. Berechnen Sie den Inhalt A | ||
| Zeile 70: | Zeile 112: | ||
c) Bestimmen Sie nun den Wert des Integrals <math>\int_{0}^{1} f (x)\,dx</math> mit Hilfe der | c) Bestimmen Sie nun den Wert des Integrals <math>\int_{0}^{1} f (x)\,dx</math> mit Hilfe der | ||
| − | Gauß’schen | + | Gauß’schen <math> \varphi </math>-Funktion(<math>\varphi(x) = \frac{1}{\sqrt{2\pi } } e^{-0,5x^2}</math>) und dem stochastischen |
Tafelwerk. Um wie viel Prozent weicht der Näherungswert aus | Tafelwerk. Um wie viel Prozent weicht der Näherungswert aus | ||
Teilaufgabe 3b von diesem Ergebnis ab? (6BE) | Teilaufgabe 3b von diesem Ergebnis ab? (6BE) | ||
{{Lösung versteckt|[[Bild:ABI_2008_II_A3c_Lös1.jpg|800px]]}} | {{Lösung versteckt|[[Bild:ABI_2008_II_A3c_Lös1.jpg|800px]]}} | ||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
Aktuelle Version vom 15. Februar 2011, 15:51 Uhr
|
Erstellt von Alistair Mainka und Benjamin Schleicher. |
Gegeben ist die Funktion a) Untersuchen Sie Gf rechnerisch auf Symmetrie und Schnittpunkte mit den Achsen. Bestimmen Sie das Verhalten von f für x → + ∞ und x → − ∞. (4BE)
b) Zeigen Sie, dass gilt:
|
Die Integralfunktion F ist definiert durch a) Untersuchen Sie das Symmetrie-, Monotonie- und Krümmungsverhalten des Graphen von F. Bestimmen Sie aus der Abbildung mit Hilfe des Gitternetzes Näherungswerte für F(0,5), F(1), F(2) und F(4). Tragen Sie den Graphen von F im Bereich x ∈[−4;4] in die gegebene Abbildung ein. (8BE)
Könnt ihr die Abbildung mit dem eingezeichneten Graphen von F noch hochladen? b) Für x > 1 gilt offensichtlich
Bemerkung:
|
Die Funktion f soll im Folgenden in einer Umgebung von x = 0 durch eine
Polynomfunktion p mit dem Term a) Bestimmen Sie die Koeffizienten a, b und c so, dass f und p an der
Stelle x = 0 im Funktionswert und in den Werten der 1. bis einschließlich
4. Ableitung übereinstimmen.
Ohne Nachweis darf verwendet werden: [Zur Kontrolle:
b) Zeigen Sie, dass p keine Nullstelle besitzt. Berechnen Sie den Inhalt A der Fläche, die von den Koordinatenachsen, dem Graphen von p und der Geraden x = 1 eingeschlossen wird, auf 4 Dezimalen gerundet. (5BE) [Zur Kontrolle: A ≈ 2,3332]
c) Bestimmen Sie nun den Wert des Integrals
|
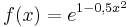 mit Definitionsbereich Df = IR .
Die Abbildung auf der folgenden Seite zeigt den Graphen Gf von f.
mit Definitionsbereich Df = IR .
Die Abbildung auf der folgenden Seite zeigt den Graphen Gf von f.
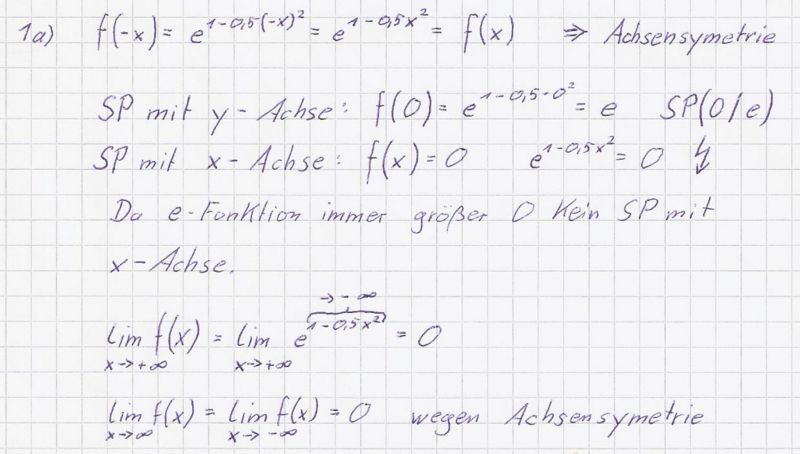
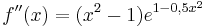 .
Bestimmen Sie durch Rechnung das Monotonieverhalten von f und die
Koordinaten der Wendepunkte. (6BE)
.
Bestimmen Sie durch Rechnung das Monotonieverhalten von f und die
Koordinaten der Wendepunkte. (6BE)
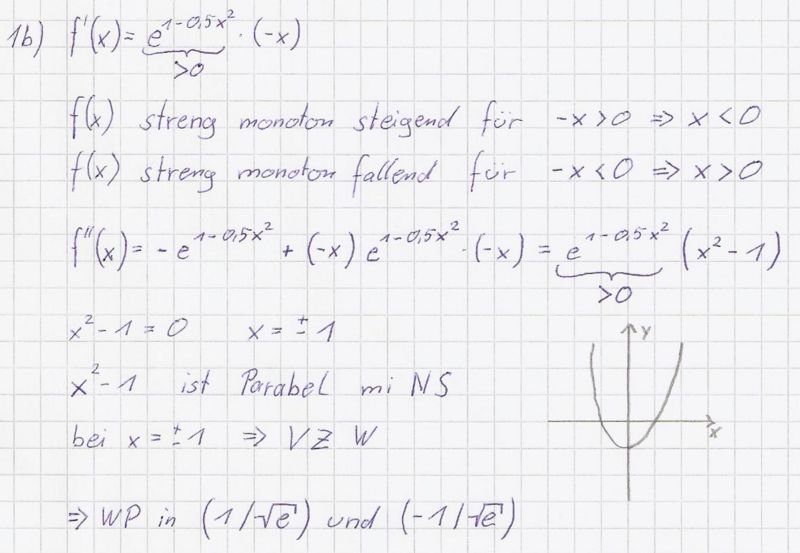
 0 (anstatt x<0), analog streng monoton fallend für x
0 (anstatt x<0), analog streng monoton fallend für x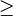 0 ?
0 ?
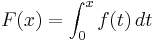 , x ∈ IR.
, x ∈ IR.

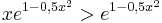 . Zeigen Sie damit,
dass
. Zeigen Sie damit,
dass 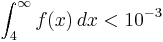 ist.
Was folgt für die Funktionswerte von F für x ≥ 4? (5BE)
ist.
Was folgt für die Funktionswerte von F für x ≥ 4? (5BE)
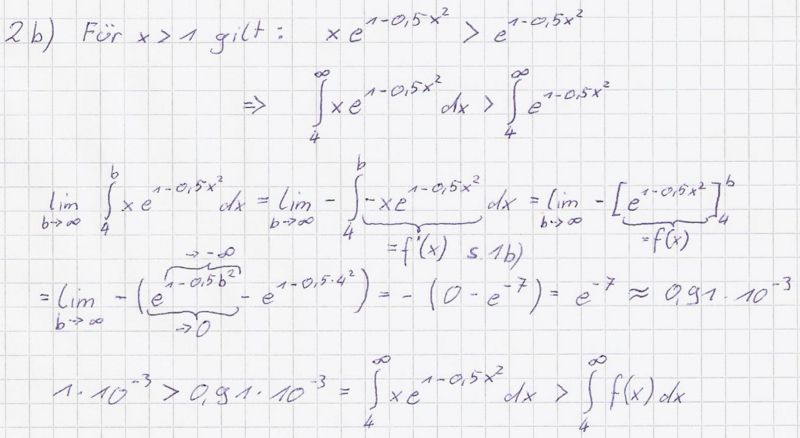
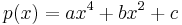 , a, b, c ∈ IR ,
angenähert werden.
, a, b, c ∈ IR ,
angenähert werden.
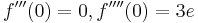 (6BE)
(6BE)
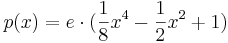 ]
]
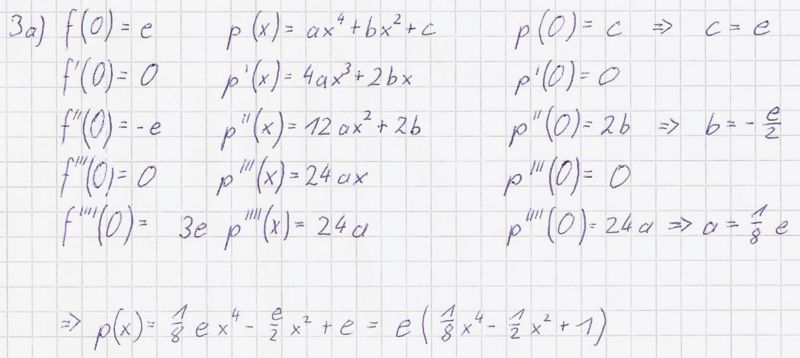
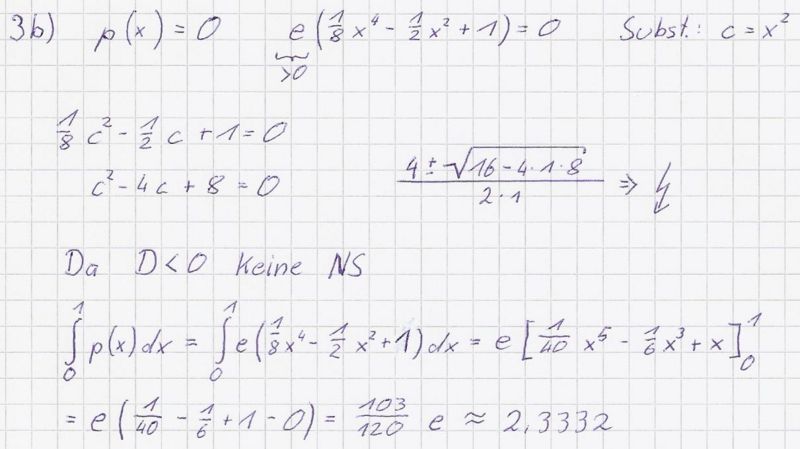
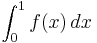 mit Hilfe der
Gauß’schen
mit Hilfe der
Gauß’schen 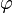 -Funktion(
-Funktion(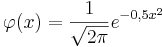 ) und dem stochastischen
Tafelwerk. Um wie viel Prozent weicht der Näherungswert aus
Teilaufgabe 3b von diesem Ergebnis ab? (6BE)
) und dem stochastischen
Tafelwerk. Um wie viel Prozent weicht der Näherungswert aus
Teilaufgabe 3b von diesem Ergebnis ab? (6BE)