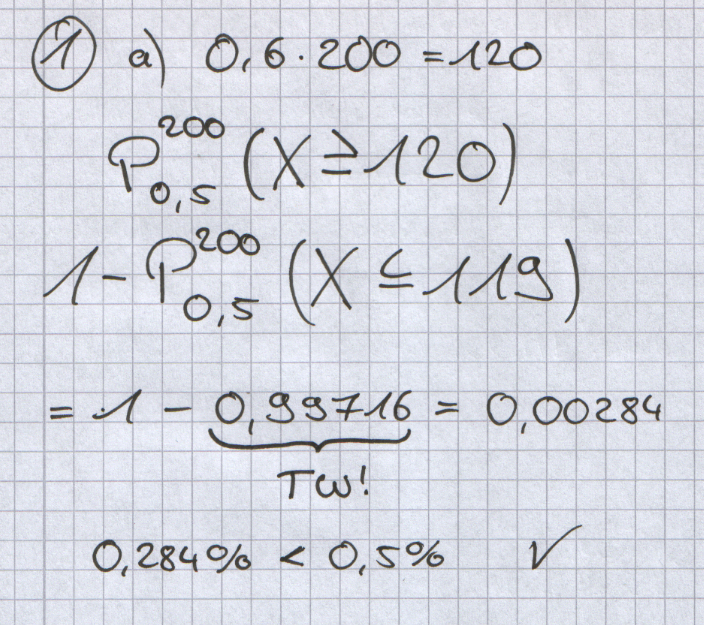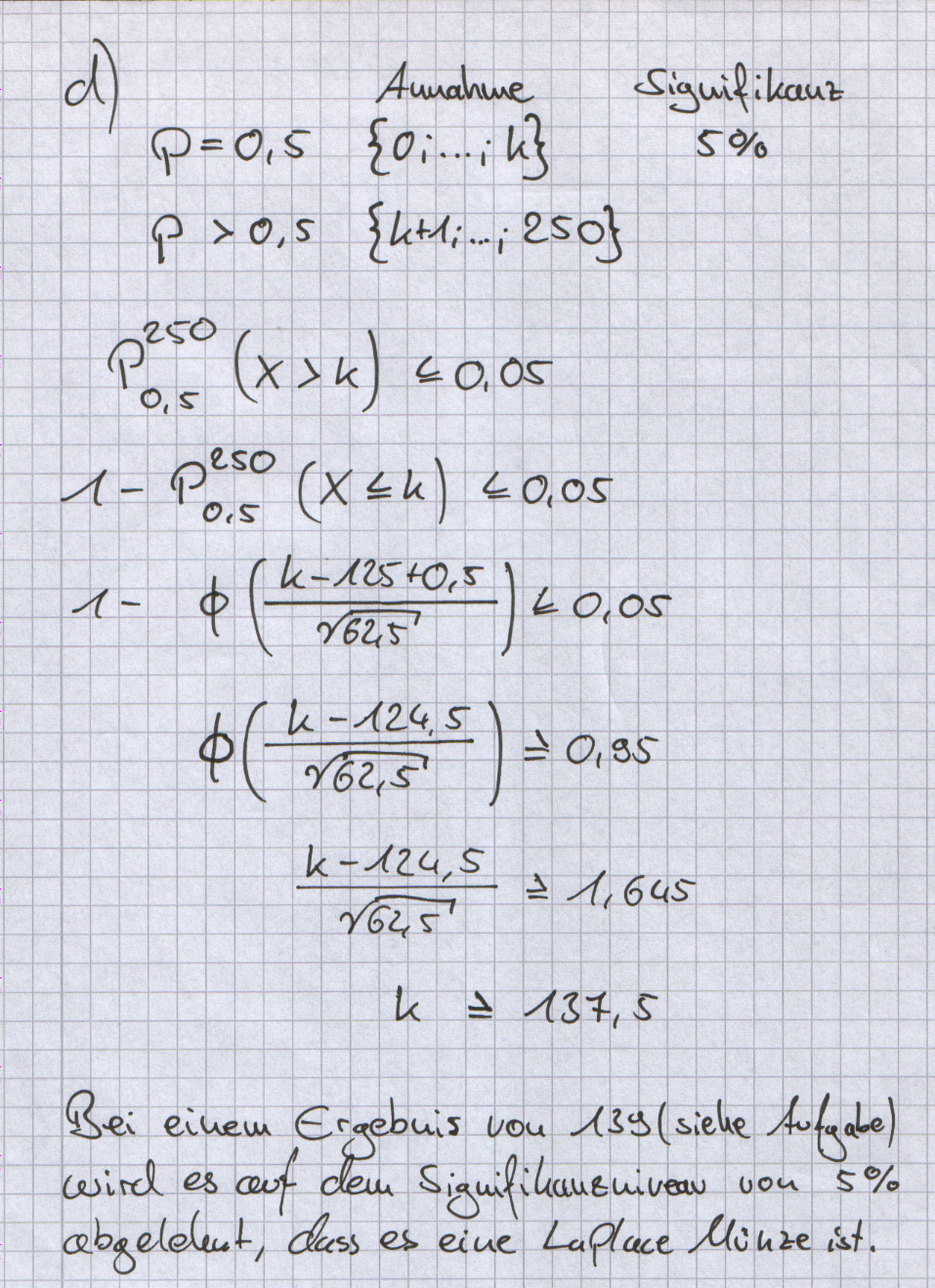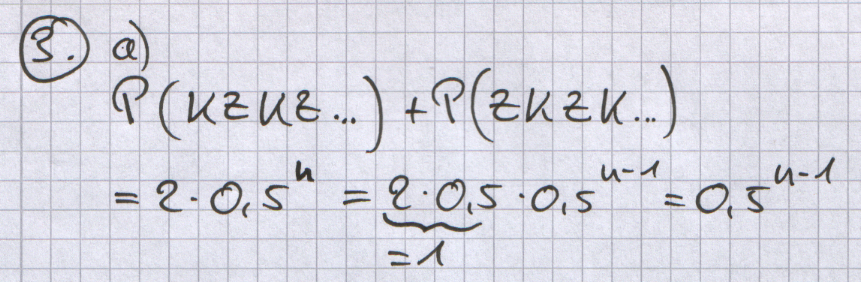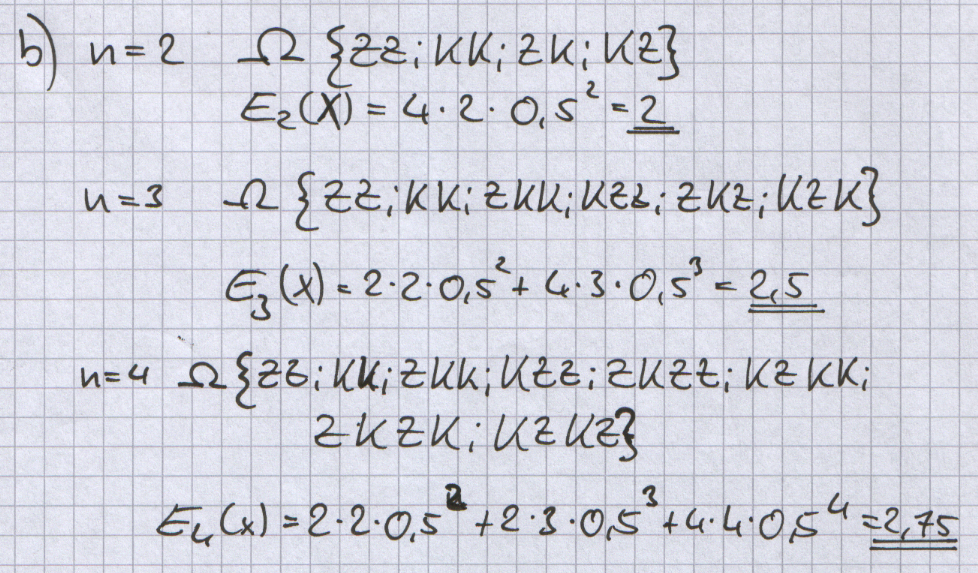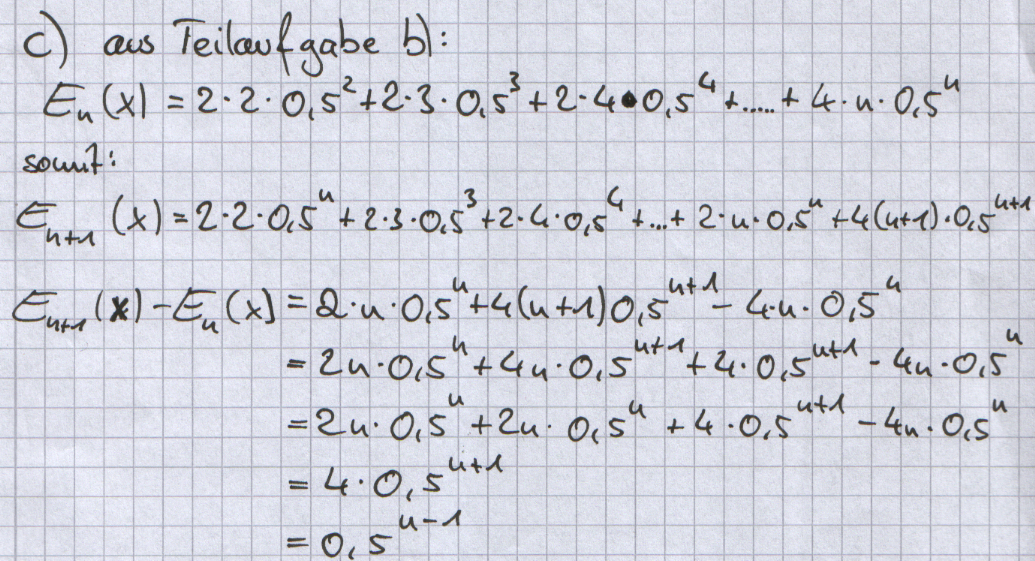2003 IV: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
 
(4 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 9: Zeile 9:
  
  
−
<center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=56690cea22e20298b306940dfaa656c6 '''Download der Originalaufgaben: Abitur 2003 LK Mathematik Bayern''']  -  [[Media:LKM Abi 2003 IV lös.doc|Lösung gesamt]]</center>
+
<center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=56690cea22e20298b306940dfaa656c6 '''Download der Originalaufgaben: Abitur 2003 LK Mathematik Bayern''']  -  [[Media:Burkard Christian_Mathlk03.pdf|Lösung gesamt]]</center>
  
  
Zeile 31: Zeile 31:
 
600-mal Zahl oben liegen geblieben.
 
600-mal Zahl oben liegen geblieben.
  
−
'''a)''' Zeigen Sie, dass der Erwartungswert der Zufallsgröße „Augenzahl beim einmaligen Werfen eines Vegas-Würfels“ 4 ist.  
+
;a)
 +
Zeigen Sie, dass bereits bei 200 Würfen einer Laplace-Münze die
 +
Wahrscheinlichkeit dafür, dass in wenigstens 60 % der Fälle Zahl
 +
oben liegen bleibt, kleiner als 0,5 % ist.
  
 
:{{Lösung versteckt|
 
:{{Lösung versteckt|
−
[[Bild:1.jpg]]
+
[[Bild:Burkard Christian_1a.jpg]]
 
}}
 
}}
  
  
−
'''b)''' bla
+
;b)
 +
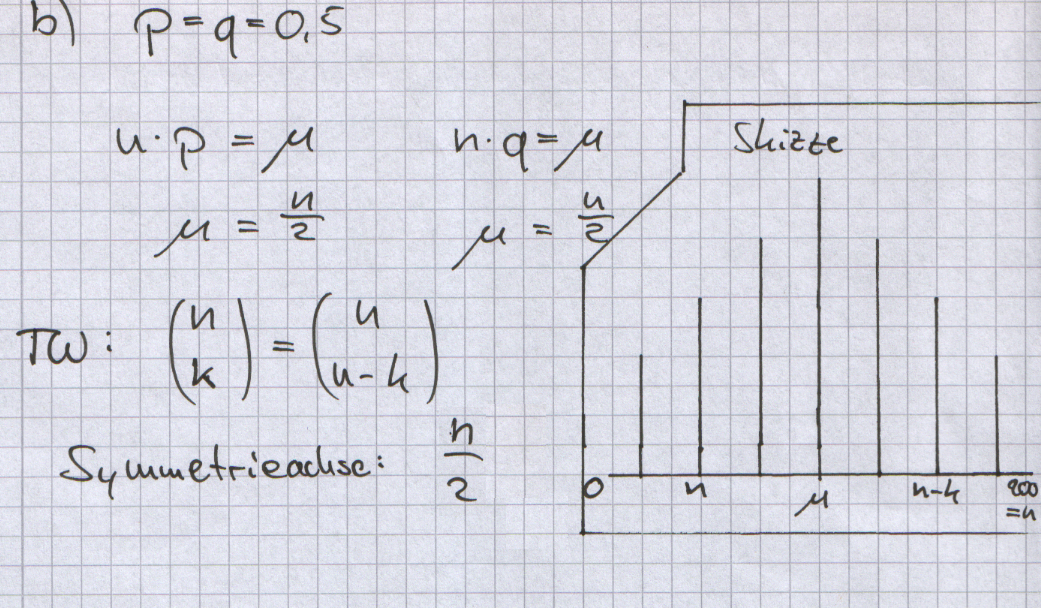
Begründen Sie, dass die Stabdiagramme der Binomialverteilungen
 +
mit p = 0,5 achsensymmetrisch sind. Geben Sie die Symmetrieachse
 +
an.
  
 
:{{Lösung versteckt|
 
:{{Lösung versteckt|
−
[[Bild:1.jpg]]
+
[[Bild:Burkard Christian_1b.jpg]]
 
}}
 
}}
  
−
'''c)''' bla
+
;c)
 +
Ermitteln Sie mit Hilfe der Ungleichung von Tschebyschow eine
 +
möglichst kleine obere Schranke für die Wahrscheinlichkeit, bei 1000
 +
Würfen einer Laplace-Münze wenigstens 600-mal Zahl zu erhalten.
 +
Vergleichen Sie diesen Wert mit dem Ergebnis aus Teilaufgabe 1a
 +
und nehmen Sie dazu kurz Stellung.
  
 
:{{Lösung versteckt|
 
:{{Lösung versteckt|
−
[[Bild:1.jpg]]
+
[[Bild:Burkard Christian_1c.jpg]]
 
}}
 
}}
  
−
'''d)''' bla
+
;d)
 +
Aufgrund des Zeitungsartikels führte ein Schüler eine eigene Versuchsreihe
 +
durch. Er ließ eine 2-Euro-Münze 250-mal auf dem Tisch
 +
kreiseln; dabei blieb 139-mal Zahl oben.
 +
Stellen Sie durch Näherung mit der Normalverteilung fest, ob dieses
 +
Ergebnis auf einem Niveau von 5 % signifikant dafür ist, dass bei
 +
dieser Münze häufiger Zahl oben liegen bleibt als bei einer Laplace-
 +
Münze.
  
 
:{{Lösung versteckt|
 
:{{Lösung versteckt|
−
[[Bild:1.jpg]]
+
[[Bild:Burkard Christian_1d.jpg]]
 
}}
 
}}
  
Zeile 67: Zeile 85:
  
 
;Aufgabe 2  
 
;Aufgabe 2  
−
Auf dem Tisch liegen ungeordnet drei Laplace-Würfel und ein Vegas-Würfel. Ein Spieler nimmt davon zufällig drei Würfel und wirft sie gleich¬zeitig.
+
Auf dem Schulfest des Laplace-Gymnasiums wurde untersucht, welchen
−
Mit welcher Wahrscheinlichkeit erzielt er drei gleiche Augenzahlen, wenn er drei Laplace-Würfel genommen hat? Mit welcher Wahrschein-lichkeit erzielt er drei gleiche Augenzahlen, wenn er zwei Laplace-Würfel und den Vegas-Würfel genommen hat?
+
Einfluss es hat, ob eine 2-Euro-Münze geworfen oder auf dem Tisch gekreiselt
−
Welche Folgerung können Sie aus Ihren Ergebnissen bezüglich der stochastischen Abhängigkeit der Ereignisse „Er erzielt drei gleiche Augenzahlen“ und „Er nimmt drei Laplace-Würfel“ ziehen?  
+
wird. Jeder Schüler durfte selbst entscheiden, ob er lieber werfen
 +
oder kreiseln wollte. In der Schülerzeitung war anschließend Folgendes
 +
zu lesen:
 +
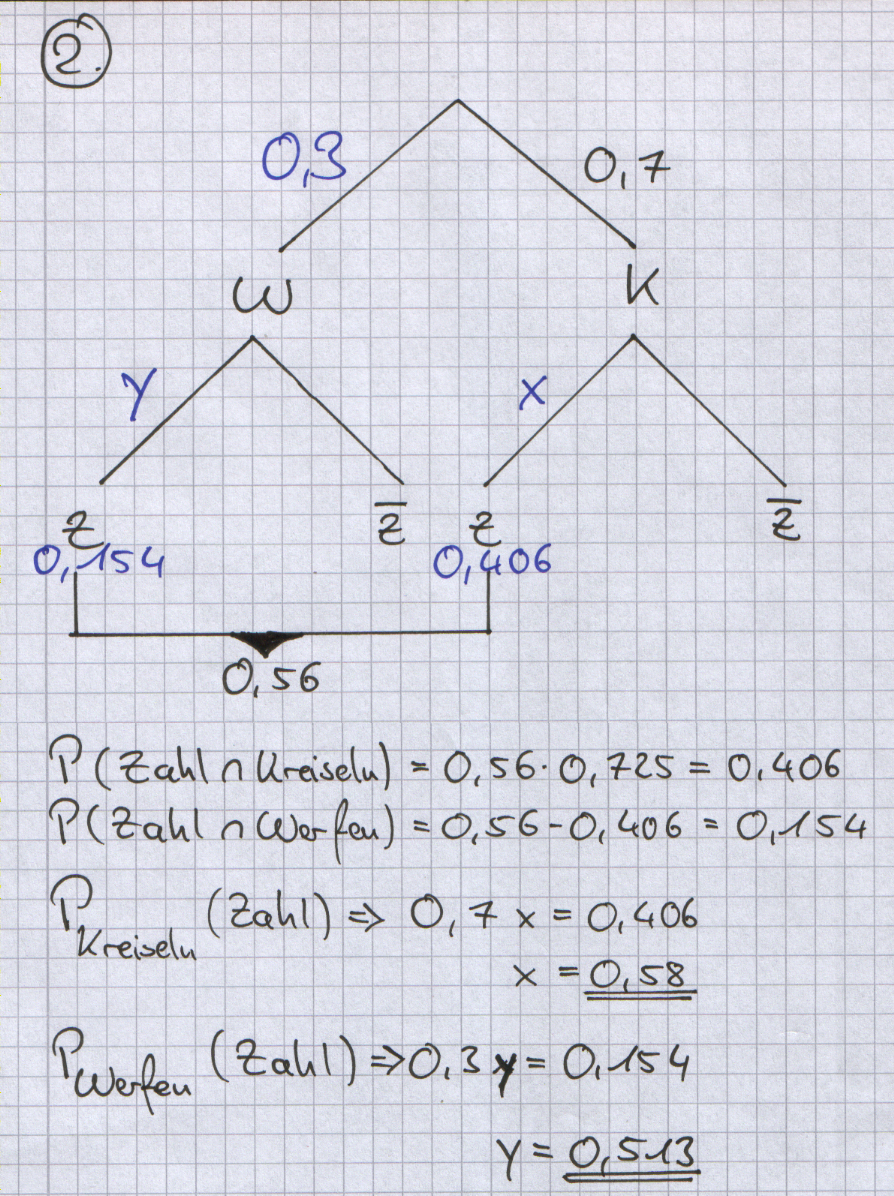
“70 % der Schüler kreiselten die Münze. Insgesamt ist in 56 % aller Fälle
 +
Zahl oben liegen geblieben, wobei davon 72,5 % durch Kreiseln erzielt
 +
worden sind.“
 +
Wie groß ist die relative Häufigkeit des Ereignisses „Zahl liegt oben“
 +
beim Werfen und wie groß ist sie beim Kreiseln?
 +
 
 
:{{Lösung versteckt|
 
:{{Lösung versteckt|
−
[[Bild:2.jpg]]
+
[[Bild:Burkard Christian_2.jpg]]
 
}}
 
}}
 
</td></tr></table></center>
 
</td></tr></table></center>
Zeile 85: Zeile 111:
  
 
;Aufgabe 3  
 
;Aufgabe 3  
−
Um bei einem Würfel festzustellen, ob es sich um einen Laplace- oder Vegas-Würfel handelt, wird er 100 mal geworfen. Ein Vegas-Würfel soll mit einer Wahrscheinlichkeit von mindestens 99 % als solcher eingestuft werden.  
+
Eine Laplace-Münze wird so oft geworfen, bis zweimal hintereinander
 +
die gleiche Seite oben liegen bleibt. Insgesamt wird aber höchstens n-mal
 +
geworfen. Die Zufallsgröße X sei die Anzahl der Würfe, E<sub>n</sub> (X) sei ihr
 +
Erwartungswert.
 
;a)
 
;a)
−
Bestimmen Sie hierzu die Entscheidungsregel anhand der Anzahl der geworfenen Sechser so, dass möglichst auch ein Laplace-Würfel richtig eingestuft wird.
+
Wie groß ist die Wahrscheinlichkeit, bei n-maligem Werfen immer
−
[Ergebnis: Entscheidung für Vegas-Würfel ab 23 geworfenen Sechsern]
+
abwechselnd beide Seiten zu erhalten?
 
:{{Lösung versteckt|
 
:{{Lösung versteckt|
−
[[Bild:jsucb_3a.jpg]]
+
[[Bild:Burkard Christian_3a.jpg]]
 
}}
 
}}
 
;b)
 
;b)
−
Mit welcher Wahrscheinlichkeit wird bei dieser Entscheidungsregel ein Laplace-Würfel falsch eingestuft?
+
Bestimmen Sie E<sub>2</sub> (X), E<sub>3</sub>(X) und E<sub>4</sub> (X) .
 
:{{Lösung versteckt|
 
:{{Lösung versteckt|
−
[[Bild:jsucb_3b.jpg]]
+
[[Bild:Burkard Christian_3b.jpg]]
 
}}
 
}}
−
</td></tr></table></center>
 
  
 +
;c)
 +
Zeigen Sie, dass gilt: E<sub>n+1</sub> (X)- E<sub>n</sub> (X) = 0,5<sup>n-1</sup>
  
−
</div>
 
−
 
−
 
−
<div style="padding:1px;background: #EEEEE6;border:0px groove;">
 
−
 
−
<center><table border="0" width="800px" cellpadding=5 cellspacing=15>
 
−
<tr><td  width="800px" valign="top">
 
−
Eine Packung des Spiels enthält – ungeordnet und äußerlich nicht unter-scheidbar – 7 Laplace- und 3 Vegas-Würfel.
 
−
;Aufgabe 4
 
−
Aus dieser Packung wird ein Würfel entnommen und 100-mal geworfen. Mit welcher Wahrschein¬lichkeit handelt es sich um einen Vegas-Würfel, wenn dabei 25-mal eine „6“ geworfen wird?
 
 
:{{Lösung versteckt|
 
:{{Lösung versteckt|
−
[[Bild:4.jpg]]
+
[[Bild:Burkard Christian_3c.jpg]]
 
}}
 
}}
−
</td></tr></table></center>
 
−
 
−
 
−
</div>
 
−
 
−
 
−
<div style="padding:1px;background: #EEEEE6;border:0px groove;">
 
−
 
−
<center><table border="0" width="800px" cellpadding=5 cellspacing=15>
 
−
<tr><td  width="800px" valign="top">
 
−
 
−
;Aufgabe 5
 
−
Die 10 Würfel werden nun einzeln nacheinander aus der Packung ent-nommen und je 100-mal geworfen.
 
−
;a)
 
−
Die Zufallsgröße X bezeichne die Anzahl der geworfenen Sechser unter den insgesamt 1000 durchzuführenden Würfen. Berechnen Sie Erwartungs¬wert und Varianz von X.
 
−
[Ergebnis: <math>E(X)=216\frac{2}{3}, Var(X) = 163\frac{8}{9}</math>  ]
 
−
:{{Lösung versteckt|
 
−
[[Bild:5a.jpg]]
 
−
}}
 
−
 
−
;b)
 
−
Die Zufallsgröße X ist näherungsweise normalverteilt. Berechnen Sie mit Hilfe der Normalverteilung, mit welcher Wahrscheinlichkeit bei den 1000 Würfen mehr als 225-mal eine „6“ geworfen wird.
 
−
:{{Lösung versteckt|
 
−
[[Bild:5b.jpg]]
 
−
}}
 
−
</td></tr></table></center>
 
−
 
−
 
−
</div>
 
−
 
−
 
−
<div style="padding:1px;background: #EEEEE6;border:0px groove;">
 
−
 
−
<center><table border="0" width="800px" cellpadding=5 cellspacing=15>
 
−
<tr><td  width="800px" valign="top">
 
−
 
−
;Aufgabe 6
 
−
Bei einem Spiel werden jeweils 5 Würfel geworfen. Aus den Augen-zahlen – aufgefasst als Ziffern – werden möglichst große fünfstellige natürliche Zahlen gebildet, z. B. 43321, nicht jedoch 34312.
 
−
;a)
 
−
Mit welcher Wahrscheinlichkeit erhält man eine Zahl größer als 50000, wenn es sich um 5 Laplace-Würfel handelt?
 
−
:{{Lösung versteckt|
 
−
[[Bild:6a.jpg]]
 
−
}}
 
−
;b)
 
−
Wie viele verschiedene natürliche Zahlen können nach dieser Spiel-regel gebildet werden? Wählen Sie aus den folgenden kombina-torischen „Modellen“ zunächst das für dieses Problem passende aus und bestimmen Sie dann mit dessen Hilfe die gesuchte Anzahl.
 
−
 
−
A) Anzahl der fünfstelligen Zahlen aus den Ziffern 1 bis 6 dividiert durch die Zahl der Permutationen von 5 Elementen
 
  
−
B) Zahl der möglichen Verteilungen von 5 Kugeln auf 6 Urnen, wobei es nur auf die jeweilige Anzahl der Kugeln in den Urnen ankommt
+
;d)
 +
Erläutern Sie, warum E<sub>n</sub> (X) für n → + ∞ nicht größer als 3 wird,
 +
und interpretieren Sie diese Tatsache im vorliegenden Zufallsexperiment.
  
−
C) Zahl der möglichen Verteilungen von 6 Kugeln auf 5 Urnen, wobei es nur auf die jeweilige Anzahl der Kugeln in den Urnen ankommt
 
 
:{{Lösung versteckt|
 
:{{Lösung versteckt|
−
[[Bild:6b.jpg]]
+
[[Bild:Burkard Christian_3d.jpg]]
 
}}
 
}}
 
</td></tr></table></center>
 
</td></tr></table></center>

Aktuelle Version vom 11. April 2010, 17:48 Uhr


Leistungskurs Mathematik (Bayern): Abiturprüfung 2003
Stochastik IV


Download der Originalaufgaben: Abitur 2003 LK Mathematik Bayern - Lösung gesamt


Erarbeitet von Christian Burkard und Julius Schmidt



Aufgabe 1

Im Januar 2002 war in einer Zeitung zu lesen, dass die neuen Euro- Münzen keine Laplace-Münzen seien. Bei einem Experiment mit einer 2-Euro-Münze, die man 1000-mal auf dem Tisch kreiseln ließ, sei 600-mal Zahl oben liegen geblieben.

a)

Zeigen Sie, dass bereits bei 200 Würfen einer Laplace-Münze die Wahrscheinlichkeit dafür, dass in wenigstens 60 % der Fälle Zahl oben liegen bleibt, kleiner als 0,5 % ist.

Burkard Christian 1a.jpg


b)

Begründen Sie, dass die Stabdiagramme der Binomialverteilungen mit p = 0,5 achsensymmetrisch sind. Geben Sie die Symmetrieachse an.

Burkard Christian 1b.jpg

c)

Ermitteln Sie mit Hilfe der Ungleichung von Tschebyschow eine möglichst kleine obere Schranke für die Wahrscheinlichkeit, bei 1000 Würfen einer Laplace-Münze wenigstens 600-mal Zahl zu erhalten. Vergleichen Sie diesen Wert mit dem Ergebnis aus Teilaufgabe 1a und nehmen Sie dazu kurz Stellung.

Burkard Christian 1c.jpg

d)

Aufgrund des Zeitungsartikels führte ein Schüler eine eigene Versuchsreihe durch. Er ließ eine 2-Euro-Münze 250-mal auf dem Tisch kreiseln; dabei blieb 139-mal Zahl oben. Stellen Sie durch Näherung mit der Normalverteilung fest, ob dieses Ergebnis auf einem Niveau von 5 % signifikant dafür ist, dass bei dieser Münze häufiger Zahl oben liegen bleibt als bei einer Laplace- Münze.

Burkard Christian 1d.jpg


Aufgabe 2

Auf dem Schulfest des Laplace-Gymnasiums wurde untersucht, welchen Einfluss es hat, ob eine 2-Euro-Münze geworfen oder auf dem Tisch gekreiselt wird. Jeder Schüler durfte selbst entscheiden, ob er lieber werfen oder kreiseln wollte. In der Schülerzeitung war anschließend Folgendes zu lesen: “70 % der Schüler kreiselten die Münze. Insgesamt ist in 56 % aller Fälle Zahl oben liegen geblieben, wobei davon 72,5 % durch Kreiseln erzielt worden sind.“ Wie groß ist die relative Häufigkeit des Ereignisses „Zahl liegt oben“ beim Werfen und wie groß ist sie beim Kreiseln?

Burkard Christian 2.jpg



Aufgabe 3

Eine Laplace-Münze wird so oft geworfen, bis zweimal hintereinander die gleiche Seite oben liegen bleibt. Insgesamt wird aber höchstens n-mal geworfen. Die Zufallsgröße X sei die Anzahl der Würfe, En (X) sei ihr Erwartungswert.

a)

Wie groß ist die Wahrscheinlichkeit, bei n-maligem Werfen immer abwechselnd beide Seiten zu erhalten?

Burkard Christian 3a.jpg

b)

Bestimmen Sie E2 (X), E3(X) und E4 (X) .

Burkard Christian 3b.jpg

c)

Zeigen Sie, dass gilt: En+1 (X)- En (X) = 0,5n-1

Burkard Christian 3c.jpg

d)

Erläutern Sie, warum En (X) für n → + ∞ nicht größer als 3 wird, und interpretieren Sie diese Tatsache im vorliegenden Zufallsexperiment.

Burkard Christian 3d.jpg


Von „http://rmg.zum.de/index.php?title=LK_Mathematik/Abitur/2003_IV&oldid=31981“