Funktionsuntersuchungen: Unterschied zwischen den Versionen
| (41 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | = Funktionsuntersuchungen = | + | {| |
| + | ! width="910" | | ||
| + | |- | ||
| + | | valign="top" | | ||
| + | = <span style="color: blue">Funktionsuntersuchungen</span> = | ||
| − | Dieses Kapitel dient zur Wiederholung der Eigenschaften der einzelnen Funktionstypen. Du solltest dir während | + | <div style="margin:0px; margin-right:90px; border: solid blue; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; "> Dieses Kapitel dient zur Wiederholung der Eigenschaften der einzelnen Funktionstypen. Du solltest dir während des Bearbeitens Notizen zu den einzelnen Funktionstypen machen, sodass am Ende ein Übersichtsblatt mit den charakteristischen Merkmalen der Funktionen entsteht. </div> <br /> |
| − | + | == <span style="color: blue">Lineare Funktionen</span> == | |
| − | == Lineare Funktionen == | + | {| |
| + | ! width="910" | | ||
| + | |- | ||
| + | | valign="top" | | ||
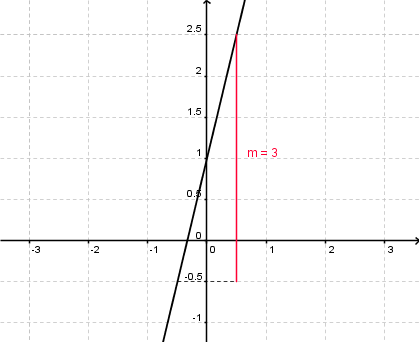
Gegeben ist die Funktion f(x)=3x+1. Bestimme zu dieser Funktion den Definitionsbereich, die Wertemenge, die Steigung m und die Schnittpunkte mit den Koordinatenachsen. Plotte den Graphen der Funktion mit GeoGebra. | Gegeben ist die Funktion f(x)=3x+1. Bestimme zu dieser Funktion den Definitionsbereich, die Wertemenge, die Steigung m und die Schnittpunkte mit den Koordinatenachsen. Plotte den Graphen der Funktion mit GeoGebra. | ||
| Zeile 10: | Zeile 17: | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
| − | D=<math>\mathbb{R}</math> | + | [[Bild:Graph5.1neu.png|450px|right]] |
| − | + | D=<math>\mathbb{R}</math> <br /> | |
| − | W=<math>\mathbb{R}</math> | + | W=<math>\mathbb{R}</math> <br /> |
| − | + | Steigung: m=3 <br /> | |
| − | Steigung: m=3 | + | Schnittpunkte mit den Koordinatenachsen: <br /> |
| − | + | :y-Achse: <br /> | |
| − | Schnittpunkte mit den Koordinatenachsen: | + | ::f(0)=3<math>\cdot</math>0+1=1 <math>\rightarrow</math> P(0/1) <br /> |
| − | + | :x-Achse: <br /> | |
| − | y-Achse: | + | ::f(x)=0 <br /> |
| − | ::f(0)= | + | ::3x+1=0 <br /> |
| − | + | ::<math>x=- \frac{1} {3}</math> <math>\rightarrow</math> <math>S \left(- \frac {1} {3}/0 \right)</math> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> | |
| − | x-Achse: | + | |
| − | + | ||
| − | ::f(x)=0 | + | |
| − | + | ||
| − | ::3x+1=0 | + | |
| − | |||
| − | |||
</popup> | </popup> | ||
| + | |} | ||
| + | <br /> | ||
| − | + | == <span style="color: blue">Quadratische Funktionen</span> == | |
| − | + | ||
| − | == Quadratische Funktionen == | + | |
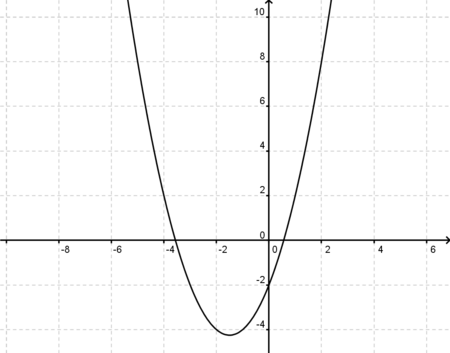
Gegeben ist die Funktion g(x)=x<sup>2</sup>+3x-2. Bestimme zu dieser Funktion Definitions- und Wertemenge, die Nullstellen und den Scheitel. Beschreibe den Verlauf des Graphen und plotte die Funktion mit GeoGebra. Vergleiche anschließend die rechnerischen Ergebnisse mit der Zeichnung. | Gegeben ist die Funktion g(x)=x<sup>2</sup>+3x-2. Bestimme zu dieser Funktion Definitions- und Wertemenge, die Nullstellen und den Scheitel. Beschreibe den Verlauf des Graphen und plotte die Funktion mit GeoGebra. Vergleiche anschließend die rechnerischen Ergebnisse mit der Zeichnung. | ||
| Zeile 39: | Zeile 39: | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
| + | [[Bild:Graph5.2.png|450px|right]] | ||
D=<math>\mathbb{R}</math> | D=<math>\mathbb{R}</math> | ||
| − | W=[-4; | + | W=[-4;∞[ |
Nullstellen: Lösungsformel | Nullstellen: Lösungsformel | ||
| Zeile 48: | Zeile 49: | ||
<math> x_{1,2} = \frac{-3\pm\sqrt{3^2+8}}{2}</math> <br /> | <math> x_{1,2} = \frac{-3\pm\sqrt{3^2+8}}{2}</math> <br /> | ||
<math> x_{1,2} = \frac{-3\pm\sqrt{17}}{2}</math> <br /> | <math> x_{1,2} = \frac{-3\pm\sqrt{17}}{2}</math> <br /> | ||
| − | x<sub>1</sub>=0,56 <math>\rightarrow</math> P<sub>1</sub>(0,56/0)<br /> | + | :x<sub>1</sub>=0,56 <math>\rightarrow</math> P<sub>1</sub>(0,56/0)<br /> |
| − | x<sub>2</sub>=-3,56 <math>\rightarrow</math> P<sub>2</sub>(-3,56/0) | + | :x<sub>2</sub>=-3,56 <math>\rightarrow</math> P<sub>2</sub>(-3,56/0) |
Graph: nach oben geöffnete Parabel | Graph: nach oben geöffnete Parabel | ||
| − | Scheitel: Die x-Koordinate des Scheitels befindet sich mittig zwischen den beiden Nullstellen <math>\rightarrow</math> x=-1,5 <br /> f(-1,5)=-4,25 <math>\rightarrow</math> S(-1,5;-4,25) | + | Scheitel: Die x-Koordinate des Scheitels befindet sich mittig zwischen den beiden Nullstellen <math>\rightarrow</math> x=-1,5 <br /> |
| + | :f(-1,5)=-4,25 <math>\rightarrow</math> S(-1,5;-4,25) | ||
| − | Oder: Quadratische Ergänzung:<br /> | + | <u>Oder:</u> Quadratische Ergänzung:<br /> |
| − | g(x)=x²+3x-2 <br /> | + | :g(x)=x²+3x-2 <br /> |
| − | g(x)=x²+3x+1,5²-1,5²-2 <br /> | + | :g(x)=x²+3x+1,5²-1,5²-2 <br /> |
| − | g(x)=(x<sup>2</sup>+3x+1,5<sup>2</sup> )-4,25 <br /> | + | :g(x)=(x<sup>2</sup>+3x+1,5<sup>2</sup> )-4,25 <br /> |
| − | g(x)=(x+1,5)<sup>2</sup>-4,25 <math>\rightarrow</math> S(-1,5/-4,25) | + | :g(x)=(x+1,5)<sup>2</sup>-4,25 <math>\rightarrow</math> S(-1,5/-4,25) |
| − | + | </popup> | |
| − | </popup> | + | <br /> <br /> |
| + | == <span style="color: blue">Ganzrationale Funktionen</span> == | ||
| − | + | Gegeben ist die Funktion h(x)=2x<sup>7</sup>-2x<sup>6</sup>+4x<sup>4</sup>-4x<sup>3</sup>. Bestimme zu dieser Funktion Definitionsbereich, Wertemenge und die Nullstellen. Untersuche die Funktion außerdem auf ihr Verhalten im Unendlichen. Kontrolliere deine Ergebnisse wieder mit GeoGebra. | |
| − | + | ||
| − | Gegeben ist die Funktion h(x)=2x<sup>7</sup>-2x<sup>6</sup>+4x<sup>4</sup>-4x<sup>3</sup>. Bestimme zu dieser Funktion Definitionsbereich, Wertemenge und die Nullstellen. Untersuche die Funktion außerdem auf ihr Verhalten im Unendlichen. Kontrolliere deine Ergebnisse wieder mit | + | |
<popup name="Lösung"> | <popup name="Lösung"> | ||
| + | [[Bild:Graph5.3.png|450px|right]] | ||
D=<math>\mathbb{R}</math> <br /> | D=<math>\mathbb{R}</math> <br /> | ||
W=<math>\mathbb{R}</math> <br /> | W=<math>\mathbb{R}</math> <br /> | ||
| Zeile 80: | Zeile 82: | ||
| − | x<sub>3</sub>=- | + | x<sub>3</sub>=-<math>\sqrt [3] 2</math> <math>\rightarrow</math> h(x)=2x<sup>3</sup> (x-1)(x<sup>3</sup>+2) |
| + | |||
| + | → P<sub>1</sub> (0/0) ; P<sub>2</sub> (1/0) ; <math>P_3 (-\sqrt [3] 2/0)</math> <br /> <br /> | ||
| + | Verhalten im Unendlichen: <br /> | ||
| + | <math>\lim_{x\to\infty} h(x)=\lim_{x\to\infty} 2x^7(1- \frac {1} {x}+ \frac {2} {x^3}- \frac {2} {x^4})=\infty</math> <br /> | ||
| + | <math>\lim_{x\to-\infty} h(x)=\lim_{x\to-\infty} 2x^7(1- \frac {1} {x}+ \frac {2} {x^3}- \frac {2} {x^4})=-\infty</math> <br /> <br /> <br /> <br /> <br /> <br /> | ||
| − | |||
| − | |||
</popup> | </popup> | ||
| + | <br /> <br /> | ||
| + | == <span style="color: blue">Gebrochen rationale Funktionen</span> == | ||
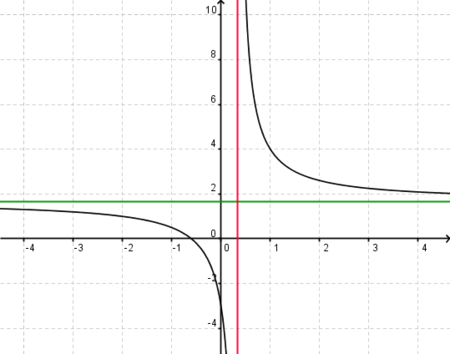
| − | + | Bestimme zu der Funktion j(x)= <math>{5x+3 \over 3x-1}</math> die Asymptoten. Folgere daraus die Definitions- und Wertemenge. Berechne außerdem die Nullstelle der Funktion. | |
| − | + | ||
| − | + | ||
| − | Bestimme zu der Funktion j(x)= <math>{5x+3 \over 3x-1}</math> die Asymptoten. Folgere daraus die | + | |
<popup name="Lösung"> | <popup name="Lösung"> | ||
| + | [[Bild:Graph5.4.png|450px|right]] | ||
Asymptoten: <br /> | Asymptoten: <br /> | ||
| − | + | <math>\lim_{x\to \pm\infty}</math><math>{5x+3 \over 3x-1}</math>=<math>\lim_{x\to \pm\infty}</math><math>{x(5+\frac 3x) \over x(3-\frac 1x)}</math> =<math>{5 \over 3}</math> <br /> | |
| − | + | ::y= <math>{5 \over 3}</math> <math>\rightarrow</math> W=<math>\mathbb{R}</math> \ <math>\left (\frac 5 3 \right)</math><br /> | |
| − | + | ::x=<math>{1 \over 3}</math> <math>\rightarrow</math> D=<math>\mathbb{R}</math> \<math>\left (\frac 1 3 \right)</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | </ | + | |
| + | Nullstelle: <br /> | ||
| + | ::j(x)=<math>{5x+3 \over 3x-1}</math> | <math>\times</math>(3x-1) <br /> | ||
| + | ::j(x)=5x+3 <br /> | ||
| + | ::x=<math>-{3 \over 5}</math> → <math>P \left(-{3 \over 5}/0 \right) </math> <br /> <br /> <br /> <br /> <br /> | ||
| + | </popup> | ||
| + | <br /> <br /> | ||
| − | == Trigonometrische Funktionen == | + | == <span style="color: blue">Trigonometrische Funktionen</span> == |
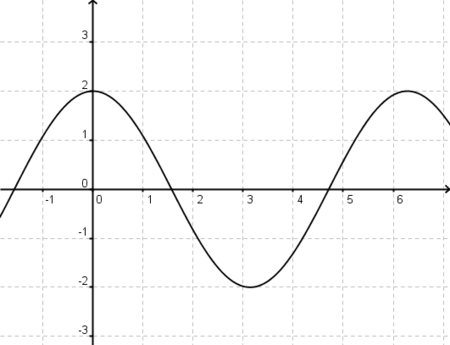
Gegeben ist die Funktion k(x)=2cosx. Bestimme den Definitionsbereich, die Wertemenge, die Amplitude und die Nullstellen. | Gegeben ist die Funktion k(x)=2cosx. Bestimme den Definitionsbereich, die Wertemenge, die Amplitude und die Nullstellen. | ||
| Zeile 113: | Zeile 118: | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
| − | D=<math>\mathbb{R}</math> <br /> | + | [[Bild:Graph5.5.png|450px|right]] |
| − | W={-2;2} <br /> | + | <br /> <br /> |
| − | Amplitude:2 | + | D=<math>\mathbb{R}</math> <br /> <br /> |
| + | W={-2;2} <br /> <br /> | ||
| + | Amplitude:2 <br /> | ||
| + | |||
| + | Nullstellen: <math>x_k=2k {\Pi \over 2}</math> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> | ||
| − | |||
| − | |||
</popup> | </popup> | ||
| + | <br /> <br /> | ||
| − | + | == <span style="color: blue">Exponentialfunktionen</span> == | |
| − | == Exponentialfunktionen == | + | |
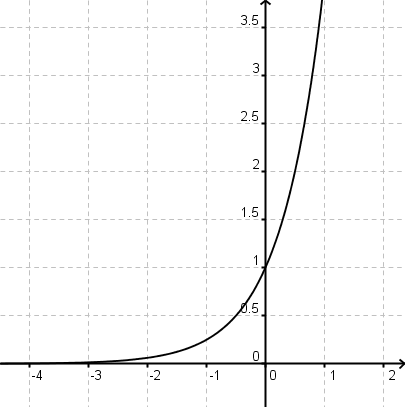
Gegeben ist die Funktion l(x)=4<sup>x</sup>. Bestimme die Definitionsmenge, den Wertebereich, die Asymptote in x-Richtung und beschreibe den Verlauf des Graphen. Vergleiche deine Ergebnisse mit dem Graphen, den dir GeoGebra liefert. | Gegeben ist die Funktion l(x)=4<sup>x</sup>. Bestimme die Definitionsmenge, den Wertebereich, die Asymptote in x-Richtung und beschreibe den Verlauf des Graphen. Vergleiche deine Ergebnisse mit dem Graphen, den dir GeoGebra liefert. | ||
| Zeile 128: | Zeile 135: | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
| − | D=<math>\mathbb{R}</math> <br /> | + | [[Bild:Graph5.6.png|450px|right]] |
| − | W=<math>\mathbb{R}</math><sup>+</sup> <br /> | + | <br /> <br /> |
| − | Graph: steigend <br /> | + | D=<math>\mathbb{R}</math> <br /> <br /> |
| − | Asymptote: x=0 <br /> | + | W=<math>\mathbb{R}</math><sup>+</sup> <br /> <br /> |
| − | + | Graph: steigend <br /> <br /> | |
| + | Asymptote: x=0 <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> | ||
| + | |||
</popup> | </popup> | ||
| + | |||
| + | |||
| + | == <span style="color: blue">Wurzelfunktionen</span> == | ||
| + | |||
| + | Gegeben ist die Funktion f(x)=<math>\sqrt x</math> . Bestimme die Definitionsmenge und die Nullstelle. <br /> <br /> | ||
| + | |||
| + | <popup name="Lösung"> | ||
| + | [[Bild:Wurzelfunktionneu.png|450px|right]] | ||
| + | D=]0;<math>\infty</math>] da unter der Wurzel keine negativen Werte stehen dürfen. | ||
| + | :f(x)=0 | ||
| + | :<math>\sqrt x</math>=0 | ||
| + | :x=0 <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> | ||
| + | </popup> | ||
| + | |} | ||
| + | <br /> <br /> | ||
| + | |||
| + | [[Facharbeit Florian Wilk/Übungsaufgaben|Weiter zum Kapitel Übungsaufgaben]] | ||
| + | |||
| + | |||
| + | [[Facharbeit Florian Wilk|Zurück zur Übersicht]] | ||
Aktuelle Version vom 27. Januar 2010, 22:25 Uhr
Funktionsuntersuchungen Dieses Kapitel dient zur Wiederholung der Eigenschaften der einzelnen Funktionstypen. Du solltest dir während des Bearbeitens Notizen zu den einzelnen Funktionstypen machen, sodass am Ende ein Übersichtsblatt mit den charakteristischen Merkmalen der Funktionen entsteht. Lineare Funktionen
Quadratische FunktionenGegeben ist die Funktion g(x)=x2+3x-2. Bestimme zu dieser Funktion Definitions- und Wertemenge, die Nullstellen und den Scheitel. Beschreibe den Verlauf des Graphen und plotte die Funktion mit GeoGebra. Vergleiche anschließend die rechnerischen Ergebnisse mit der Zeichnung.
Ganzrationale FunktionenGegeben ist die Funktion h(x)=2x7-2x6+4x4-4x3. Bestimme zu dieser Funktion Definitionsbereich, Wertemenge und die Nullstellen. Untersuche die Funktion außerdem auf ihr Verhalten im Unendlichen. Kontrolliere deine Ergebnisse wieder mit GeoGebra.
Gebrochen rationale FunktionenBestimme zu der Funktion j(x)=
Trigonometrische FunktionenGegeben ist die Funktion k(x)=2cosx. Bestimme den Definitionsbereich, die Wertemenge, die Amplitude und die Nullstellen.
ExponentialfunktionenGegeben ist die Funktion l(x)=4x. Bestimme die Definitionsmenge, den Wertebereich, die Asymptote in x-Richtung und beschreibe den Verlauf des Graphen. Vergleiche deine Ergebnisse mit dem Graphen, den dir GeoGebra liefert.
WurzelfunktionenGegeben ist die Funktion f(x)= |

 0+1=1
0+1=1  P(0/1)
P(0/1) 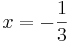
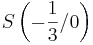
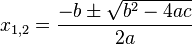
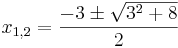
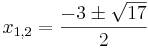

![\sqrt [3] 2](/images/math/e/c/a/eca0e705b1d86d4b1542e5d33b6f1d73.png)
![P_3 (-\sqrt [3] 2/0)](/images/math/0/0/2/0020c54ad440143f1a5c7da7b7a56b4d.png)
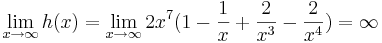
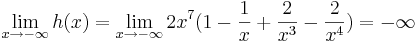
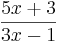 die Asymptoten. Folgere daraus die Definitions- und Wertemenge. Berechne außerdem die Nullstelle der Funktion.
die Asymptoten. Folgere daraus die Definitions- und Wertemenge. Berechne außerdem die Nullstelle der Funktion.
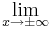
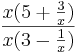 =
=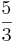
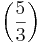
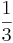
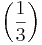
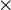 (3x-1)
(3x-1) 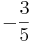 →
→ 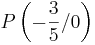
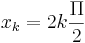
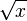 . Bestimme die Definitionsmenge und die Nullstelle.
. Bestimme die Definitionsmenge und die Nullstelle. 
 ] da unter der Wurzel keine negativen Werte stehen dürfen.
] da unter der Wurzel keine negativen Werte stehen dürfen.

