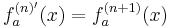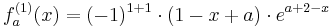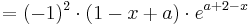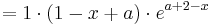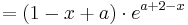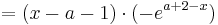Lösung von Teilaufgabe e
Aus RMG-Wiki
< Facharbeit Andre Etzel | Teilaufgabe e
Version vom 21. Januar 2010, 01:27 Uhr von Andre Etzel (Diskussion | Beiträge)
Beweisführung zur n-ten Ableitung der Funktion 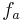 durch vollständige Induktion
durch vollständige Induktion
Hilfe zur vollständigen Induktion
Beweise, dass
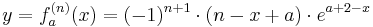 die n-te Ableitung von
die n-te Ableitung von 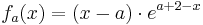 ist. (Behauptung)
ist. (Behauptung)
Beweis durch vollständige Induktion:
1. Induktionsanfang:
Die erste Ableitung ist: 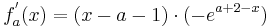 (siehe Teilaufgabe a / Extrempunkte)
(siehe Teilaufgabe a / Extrempunkte)
Die Behauptung stimmt damitmit überein:
2. Induktionsschritt:
Anfangsgleichung: 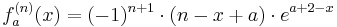
Zielgleichung: 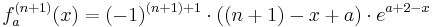
Wenn die n-te Ableitung von fa für n stimmt, muss sie auch für n+1 stimmen.
Dies soll nun bewiesen werden.
Der Beweis stimmt wenn